Za młodu interesowałem się byłem rozmaitymi algorytmami. Jednym z nich jest Game of Life - napiszę dziś króciutko cóż to takiego. Temat jest wprawdzie oklepany do bólu, ale ponieważ to mój blog, będę pisał nawet o dupie Maryni i gówno komu do tego 🙂
Game of Life (będę używał skrótu GoL bom leniw) to automat komórkowy, w wersji klasycznej dwuwymiarowy. "Gra" odbywa się na płaszczyźnie podzielonej na kwadratowe pola. Każde pole może zawierać maksymalnie jedną "żywą" bakterię (zwyczajowo oznacza się "żywe" pola na czarno a "martwe", tj. bez bakterii - na biało). No i teraz najciekawsze:
1. Jeżeli bakteria ma mniej niż dwóch sąsiadów (tzn. "żywych" sąsiadów), w następnym pokoleniu umiera z nudów.
2. Jeżeli bakteria ma więcej niż trzech sąsiadów, w następnym pokoleniu umiera z powodu tłoku.
3. Jeżeli bakteria ma dwóch lub trzech sąsiadów, przeżywa do następnego pokolenia.
4. Wreszcie, jeżeli puste pole jest otoczone przez dokładnie trzy bakterie, w następnym pokoleniu rodzi się na tym polu bakteria.
Proste, prawda? Spójrzmy na przykłady:
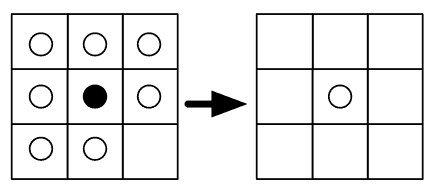
W poniższym przykładzie, środkowa bakteria umiera z powodu tłoku:
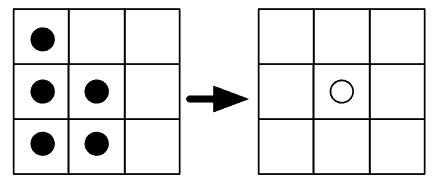 Co prawda przykład jest nie do końca jednoznaczny, ponieważ oprócz środkowej bakterii, która umiera, powyżej niej powinna urodzić się nowa, jako że w poprzednim pokoleniu komórka jest otoczona przez trzech sąsiadów. Ponadto, bakteria poniżej powinna przeżyć, ponieważ ma dokładnie trzech sąsiadów. Jednak nie wiemy tego na pewno, bo widać tylko mały fragment "świata", o rozmiarach 3x3 - skrajne komórki mogą mieć sąsiadów, których tutaj nie widać.
Co prawda przykład jest nie do końca jednoznaczny, ponieważ oprócz środkowej bakterii, która umiera, powyżej niej powinna urodzić się nowa, jako że w poprzednim pokoleniu komórka jest otoczona przez trzech sąsiadów. Ponadto, bakteria poniżej powinna przeżyć, ponieważ ma dokładnie trzech sąsiadów. Jednak nie wiemy tego na pewno, bo widać tylko mały fragment "świata", o rozmiarach 3x3 - skrajne komórki mogą mieć sąsiadów, których tutaj nie widać.
Tak czy siak, środkowa bakteria umiera bo ma za dużo sąsiadów.
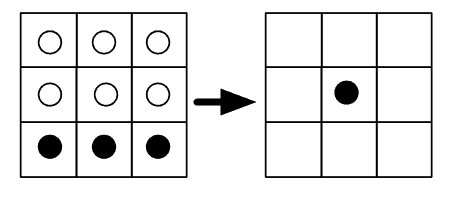
Kolejny przykład:
Tu środkowa komórka również "umiera", tym razem z nudów.
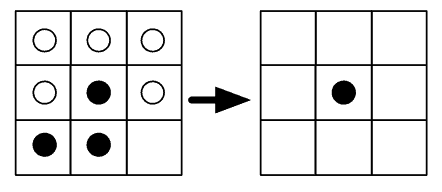
I jeszcze dwa przykłady:
W przykładzie po lewej, środkowa komórka przeżywa ponieważ ma dokładnie dwóch sąsiadów. W przykładzie po prawej na środkowym polu rodzi się nowa komórka, ponieważ w poprzednim pokoleniu pole miało dokładnie trzech sąsiadów.
W zasadzie to wszystko jeśli chodzi o reguły. Czy da się z tego wycisnąć coś ciekawego?
Otóż da się. Okazuje się bowiem, że w zależności od początkowego ustawienia da się uzyskać całkiem ciekawe "kolonie" komórek. Zacznijmy od bardzo prostego przykładu:
To tak zwany "szybowiec". Proszę zwrócić uwagę, że po czterech pokoleniach komórki są ułożone w identyczny sposób jak na początku, ale są przesunięte o jedno pole w prawo i w dół. A więc jest to "nieśmiertelna" konstrukcja, która bezustannie wędruje, o tak:
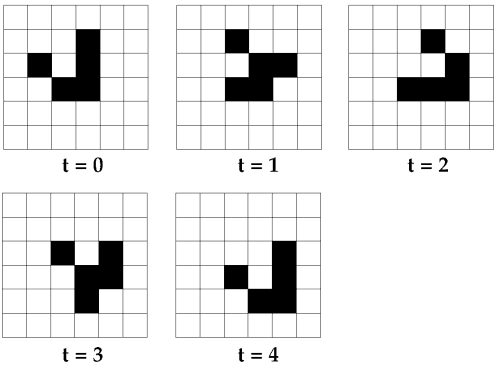
Kolejna, jeszcze prostsza konstrukcja to tzw "światła uliczne", trzy komórki obok siebie, które w kolejnych pokoleniach przeskakują między układem pionowym i poziomym:
Światła uliczne to najprostszy oscylator, czyli układ, który powraca do ustawienia wyjściowego w skończonej liczbie kroków. Innym prostym oscylatorem jest żabka:
Nieco bardziej skomplikowanym oscylatorem jest krokodyl, który potrzebuje piętnastu cykli żeby powrócić do ustawienia początkowego:
Znajdowanie oscylatorów jest zadaniem dość trudnym obliczeniowo. Oscylator z największą dotychczas znaną liczbą cykli to white shark, który replikuje się po ponad stu pięćdziesięciu milionach cykli.
Jeszcze jeden interesujący oscylator (177 cykli):
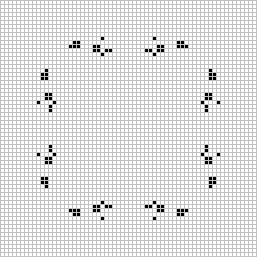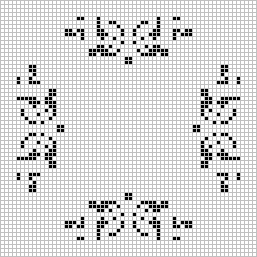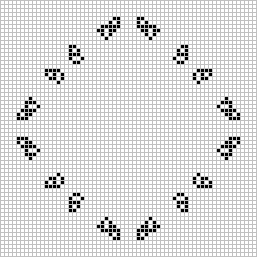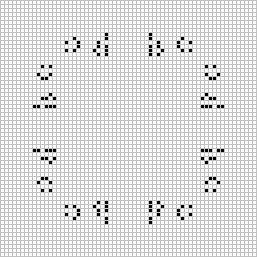
Inną kategorią układów są tak zwane "matuzalemy", czyli układy, które stabilizują się po bardzo dużej liczbie cykli.
Bardzo efektowne są tzw "breedery" czyli wielkie układy przemieszczające się w nieskończoność i pozostawiające za sobą "ślad" w postaci innych aktywnych struktur. Poniżej przykład takiego breedera:

Szczytowym osiągnięciem GoL jest implementacja za jej pomocą pełnej Maszyny Turinga, która - jak Czytelnik zapewne pamięta ze studiów - jest funkcjonalne równoważna dowolnemu komputerowi (a więc może przeprowadzać dowolnie skomplikowane obliczenia). Nie oznacza to oczywiście, że jest to "komputer" jakoś wybitnie szybki - zasymulowanie pojedynczego cyklu procesora za pomocą GoL zajmuje ponad 11 tysięcy cykli. Jest to tak zwana Paul Rendell's Turing Machine. Z wielkiej wysokości wygląda o tak:
GoL doczekała się również wersji planszowej. Co prawda nie za bardzo wyobrażam sobie, żeby dało się w to grać dłużej niż kilkanaście minut, ale jeżeli ktoś jest fanatykiem (i znajdzie drugiego takiego samobójcę), czemu by nie...
Na koniec jeszcze opowiem o wariantach GoL. Po pierwsze, można eksperymentować ze zmianą warunków narodzin, przeżywalności i śmierci - w miarę ciekawie jest jeszcze w sytuacji, kiedy oryginalne reguły zmodyfikuje się nieco i doda przepis mówiący, że nowa bakteria rodzi się nie tylko przy trzech ale i przy sześciu sąsiadach.
Dalsze modyfikacje polegają na użyciu komórek innych niż kwadratowe. Jedyne rozsądne warianty wśród wielokątów foremnych to trójkąty i sześciokąty, jednak prowadzi się też eksperymenty ze światami wypełnionymi komórkami niesymetrycznymi.
Można wreszcie eksperymentować z dodaniem kolejnego wymiaru. Przy założeniu, że w 3D pojedyncza komórka jest sześcianem, każda komórka ma 26 sąsiadów, a więc ilość możliwych warunków narodzin, przeżywania i śmierci jest nieporównanie większa niż w dwóch wymiarach. A przecież oprócz sześcianów można jeszcze kombinować z czternastościanami albo - zgodnie z badaniami Weaire-Phelan - mieszkanką dwunastościanów i czternastościanów. Albo z bryłami wypełniającymi przestrzeń nieregularnie.
A jak się już ktoś konkretnie napije, może zacząć kombinować w większej niż trzy ilości wymiarów. Ale to już całkiem inna opowieść 😉
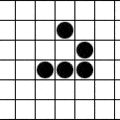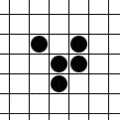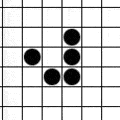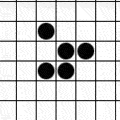

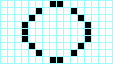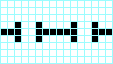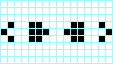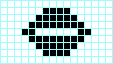
Jako że w liceum byłem w klasie biolchem tośmy się z kumplem w ramach łączenia przyjemnego (komputer! PC! 386!!) z pożytecznym (biologia!) bawiliśmy w te różne konfiguracje 🙂 Ale do breederów to nie doszliśmy 🙂
W pierwszym skanie wyłapałem tylko "z kumplem", "przyjemnego", "bawiliśmy" i "doszliśmy". Czy trzeba mnie już izolować? 😉
386 to był potwór obliczeniowy dostępny tylko tym najbogatszym. Nam, maluczkim, pozostawały 80186 (ew. jego odpowiednik NEC V20). I pewnie jeszcze miałeś Herculesa, burżuju?
To był kumpla komputer, ja wtedy miałem Amigę 🙂 Jego tata miał doktorat z matematyki więc taki mainframe w domu był uzasadniony. I AFAIK miał 2 mega RAM (komputer, nie tata)
O żeż. 2 MB to faktycznie potentat. Pamiętam, że Civilization I tego wymagało. I trzeba było formatować dyskietkę na 1.8 MB żeby się cała gra zmieściła (a i tak trzeba było wywalić pliki z niepotrzebnymi animacjami).
🙂
W Civ I grałem na Amidze. 4 dyskietki więc trochę wachlowania było. Ale się grę odpalało, ustalało warunki początkowe i szło się do kuchni zrobić coś do jedzenia bo a) komp i tak nie był do użycia b) jak się zaczęło grać to nie ma zmiłuj. Komputer w tym czasie wygenerował co miał wygenerować. I zaczynała się GRA!
A RAM gdy kupowałem peceta (1994) miał prosty przelicznik: 1 megas = 1 milion złotych 🙂 Chyba na szafie mam jeszcze te pamięci po bańce 🙂
Wersja na PC była w oryginale na dwóch dyskietkach, jednak (jak już wspomniałem) dało się to upchać na jedną, pod warunkiem że się tą jedną sformatowało gęściej, no i że się umiejętnie wywaliło parę plików.
Nawet nie wiedziałem, że była wersja na Amisię.
Btw Civ I przysłużyła mi się przy biciu prywatnego (dość niechlubnego) rekordu z serii "ile najdłużej wytrzymałeś bez spania?". Połączenie służby wojskowej (dużo rozrywek, mało snu) z Civ I okazało się strzałem w dziesiątkę. Trzy doby bez zmrużenia oka. Nigdy więcej. Nie dość, że człowiek potem pada jak martwy, to jeszcze na ogół pachnie jak Laboratoire Garnier le Skunx.
O kurka!!! 2MB RAM!!! Nie musiał pożyczać od kumpli, żeby Worda 2.0 zainstalować…. Czad…
Faktycznie, to było ciekawe zjawisko. Word 2.0 działał na jednym MB pamięci, o ile się go już zainstalowało. Haczyk polegał na tym, że instalator wymagał 2MB. A więc trzeba było iść do kolegi (który też miał 1MB) i
zabraćpożyczyć od niego tę pamięć na parę chwil. No ubaw po pachy,Czy to nie dowód na nieistnienie maszyny czasu?
XYZ-r.2034