Lewoskrętnie

https://xpil.eu/RQoRc 📋

Jeżeli zaglądasz tutaj częściej niż raz na rok, prawdopodobnie kojarzysz, że od czasu do czasu bawię się w algorytmiczne generowanie losowo wyglądających ścieżek, używając najrozmaitszych reguł na długość kroku, kąt zakrętu i tym podobne. Na ogół reguły te związane są albo z numerem bieżącego kroku (zwiększanym od jedynki w górę), albo - jak w przypadku Mrówki Langdona - z kolorem pola, na którym się aktualnie znajdujemy (o ile w ogóle są jakieś pola).

Niedawno natknąłem się na artykuł, którego autor opisuje następujący algorytm:

1. Zaczynamy w punkcie (0,0)
2. Robimy krok naprzód, o długości 1
3. Jeżeli aktualny numer kroku dzieli się przez 7 lub zawiera cyfrę 7, skręcamy w lewo o kąt prosty.
4. Przechodzimy do punktu 2, chyba że nam się znudziło, wtedy kończymy i podziwiamy widoki.

Proste, prawda?

Haczyk tkwi w punkcie 3: zawiera on bowiem dwie całkiem niespokrewnione ze sobą reguły, których połączenie sprawia, że wyznaczona w ten sposób trasa staje się mocno nieprzewidywalna.

Zacząłem bawić się kodem i osiągnąłem ciekawe (acz kompletnie bezużyteczne) rezultaty.

Zacznijmy od kodu bazowego:

import matplotlib.pyplot as plt

x, y, step_counter, direction = 0, 0, 0, 0  # 0: up, 1: left, 2: down, 3: right
denom = 7
step_limit = 10
xcoords, ycoords = [x], [y]
dirs = [(0, 1), (-1, 0), (0, -1), (1, 0)]
nth = 1 if step_limit < 10000 else step_limit // 10000


def is_turn(step):
    return step % denom == 0 or str(denom) in str(step)


while step_counter < step_limit:
    step_counter += 1
    dx, dy = dirs[direction]
    x += dx
    y += dy

    if step_counter % nth == 0 or step_counter == step_limit:
        xcoords.append(x)
        ycoords.append(y)

    if is_turn(step_counter):
        direction = (direction + 1) % 4

plt.figure(figsize=(10, 10))
plt.plot(xcoords, ycoords, marker='o', markersize=1, linestyle='-')
plt.plot(xcoords[0], ycoords[0], 'go', markersize=10, label='First Step')
plt.plot(xcoords[-1], ycoords[-1], 'ro', markersize=10, label='Last Step')

plt.axis('equal')
plt.grid(False)
plt.show()

Uwaga: od tej pory będę używał powyższego kodu do wszystkich pozostałych przykładów; jedyne modyfikacje dotyczyć będą linii numer 4 i 5: w linii 4 ustalamy podzielnik (w oryginalnym problemie: 7), a w linii 5 - liczbę kroków, po której uznajemy, że się nam znudziło.

Efekt wykonania powyższego kodu:

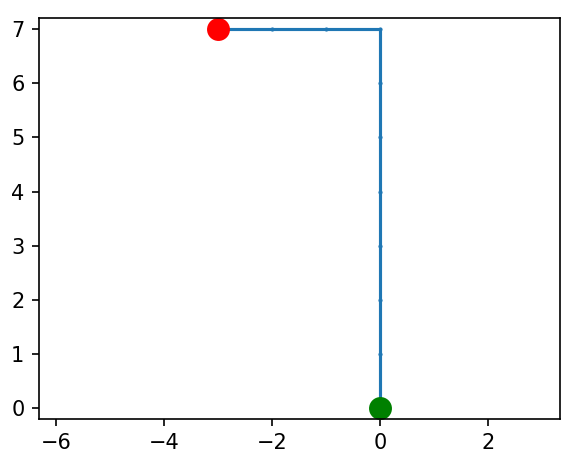
Wszystko się zgadza: po siedmiu krokach nastąpił zwrot w lewo i kolejne 3 kroki. Zwiększymy teraz liczbę kroków:

denom = 7
step_limit = 100

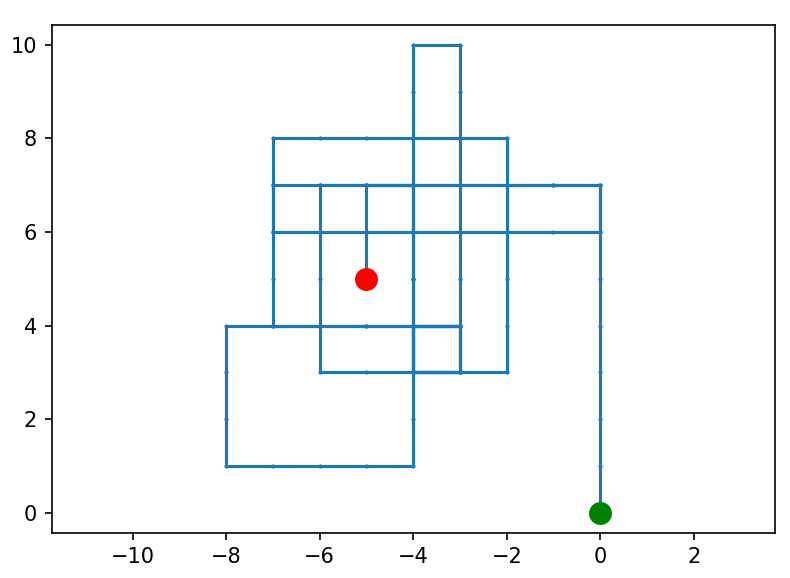
Zaczyna się robić nieco chaotycznie. Sprawdźmy teraz jak to wygląda kolejno dla 1000, 10000 i 100000 kroków:

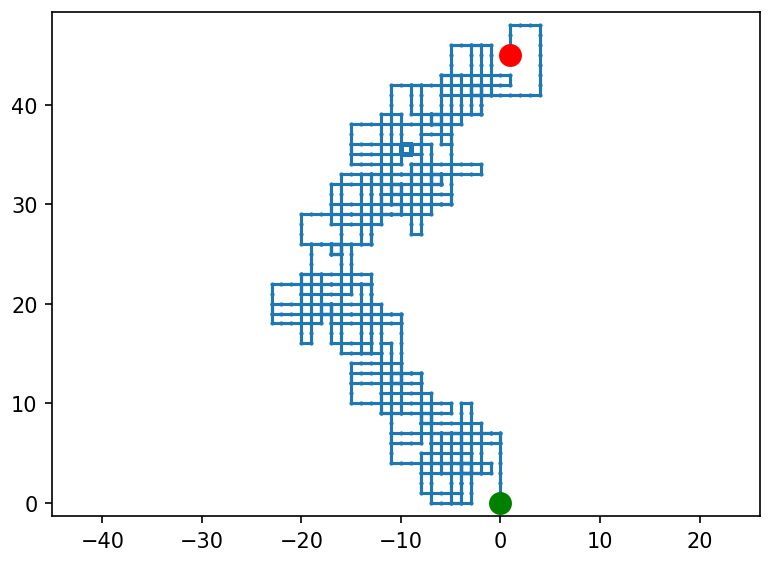
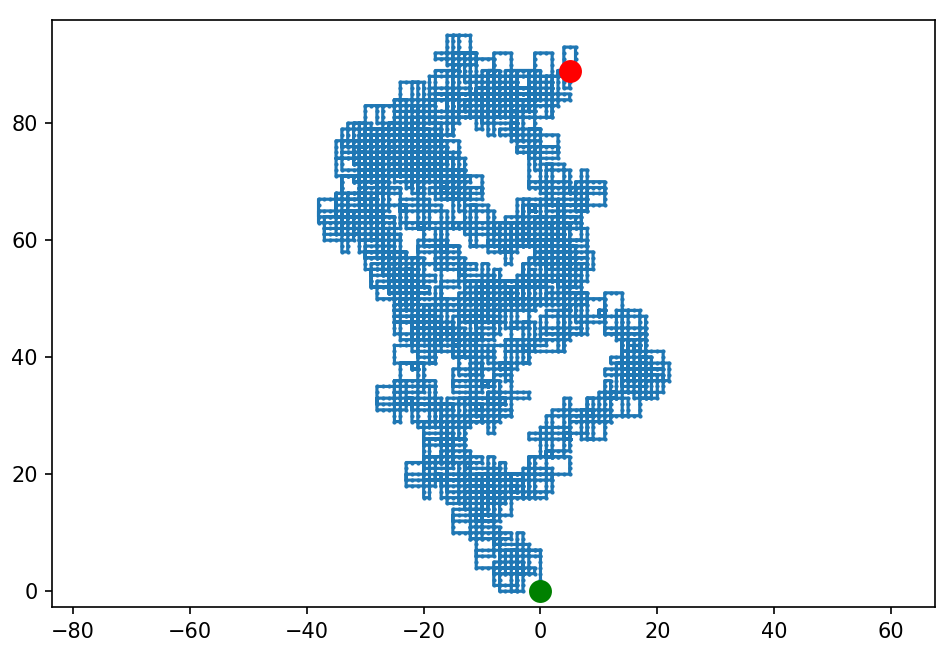
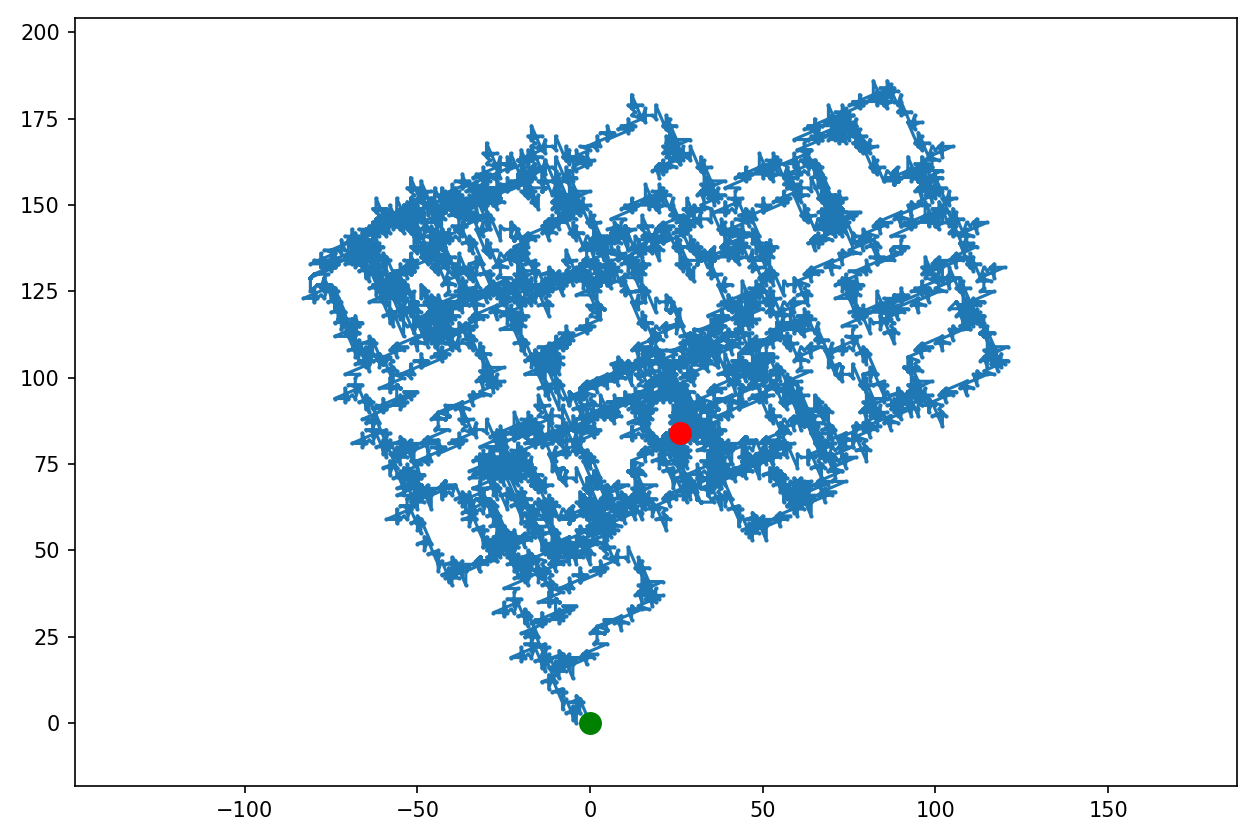
Ostatni rysunek różni się od poprzednich jakościowo - pojawiły się ukośne linie. Jakim cudem? A no takim, że jeżeli trasa zawiera więcej niż 10000 punktów, nie rysujemy każdej kropki tylko co-którąś, żeby nie przeciążyć silnika graficznego.

A teraz skoczmy od razu o trzy rzędy wielkości w górę i sprawdźmy jak to wygląda dla 100 milionów kroków:

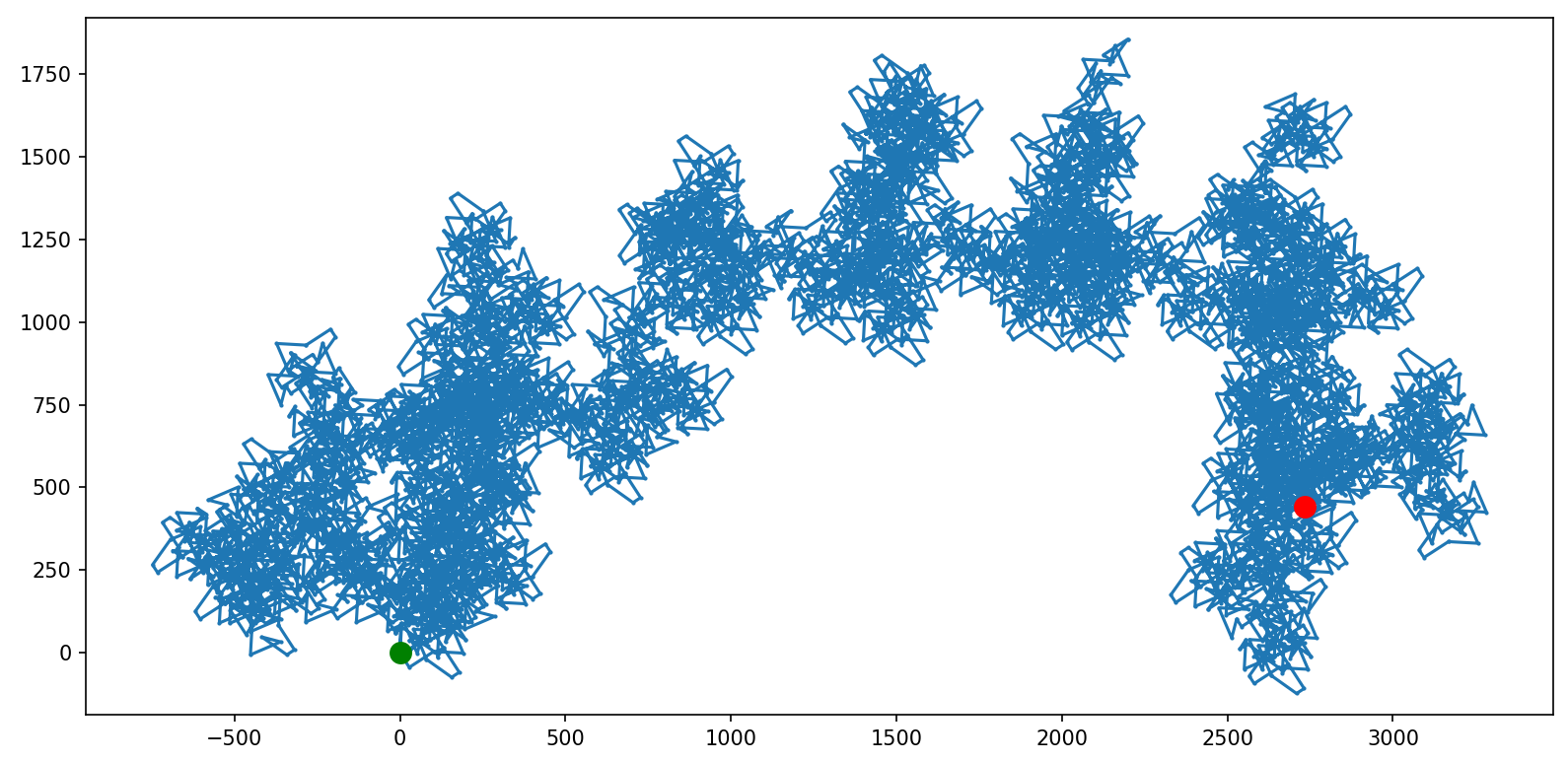
Zaczyna to pachnieć jakimś fraktalem! Nie miałem jednak wystarczająco dużo cierpliwości, żeby próbować z większymi liczbami kroków.

Ale przecież nikt nie nakazuje nam używać akurat siódemki. Sprawdźmy jak to wygląda dla innych podzielników. Od razu mówię, że dwójka, trójka, czwórka i piątka są "nudne", a więc albo zapętlają się na bardzo małej powierzchni, albo uciekają w nieskończoność po linii prostej (tzn. po linii łamanej, która z większej odległości wygląda jak prosta). Ale przy szóstce coś się zaczyna dziać:

denom = 6
step_limit = 10000

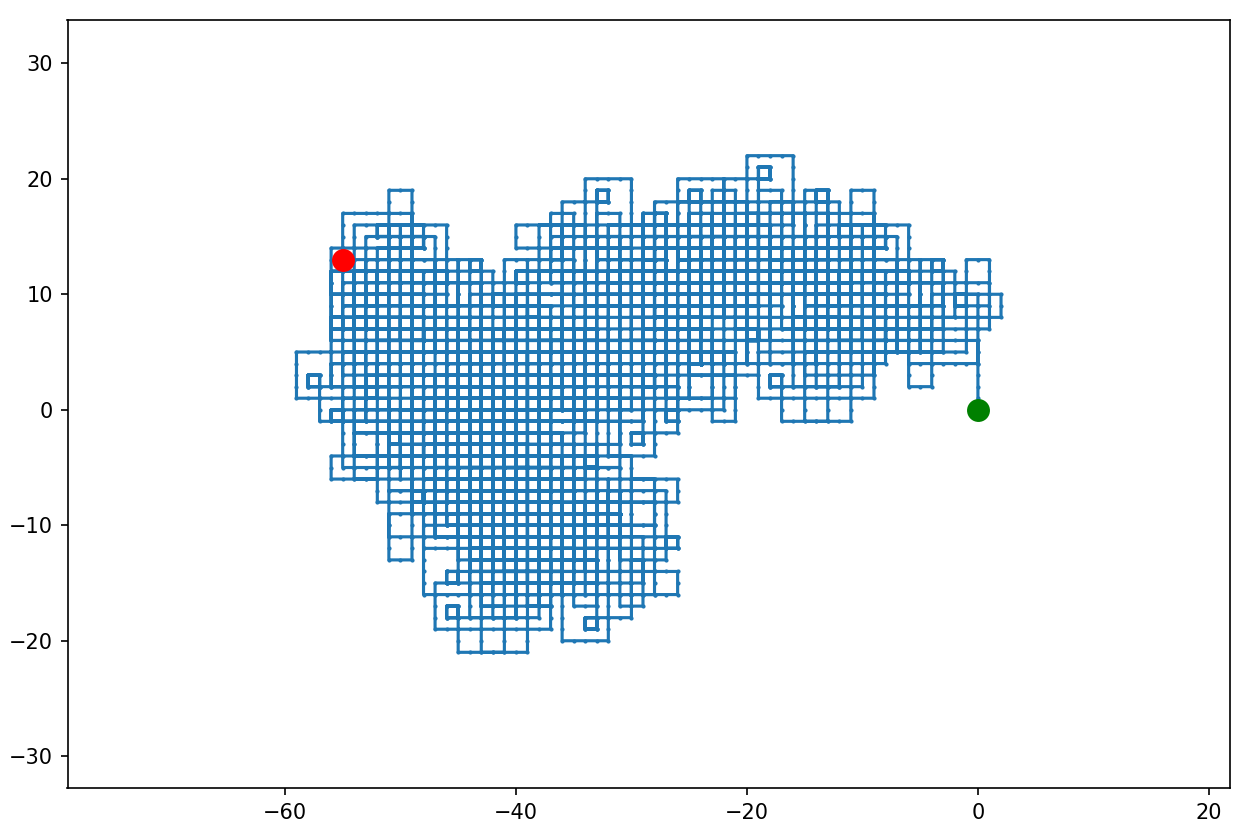
Zwiększamy limit stukrotnie...

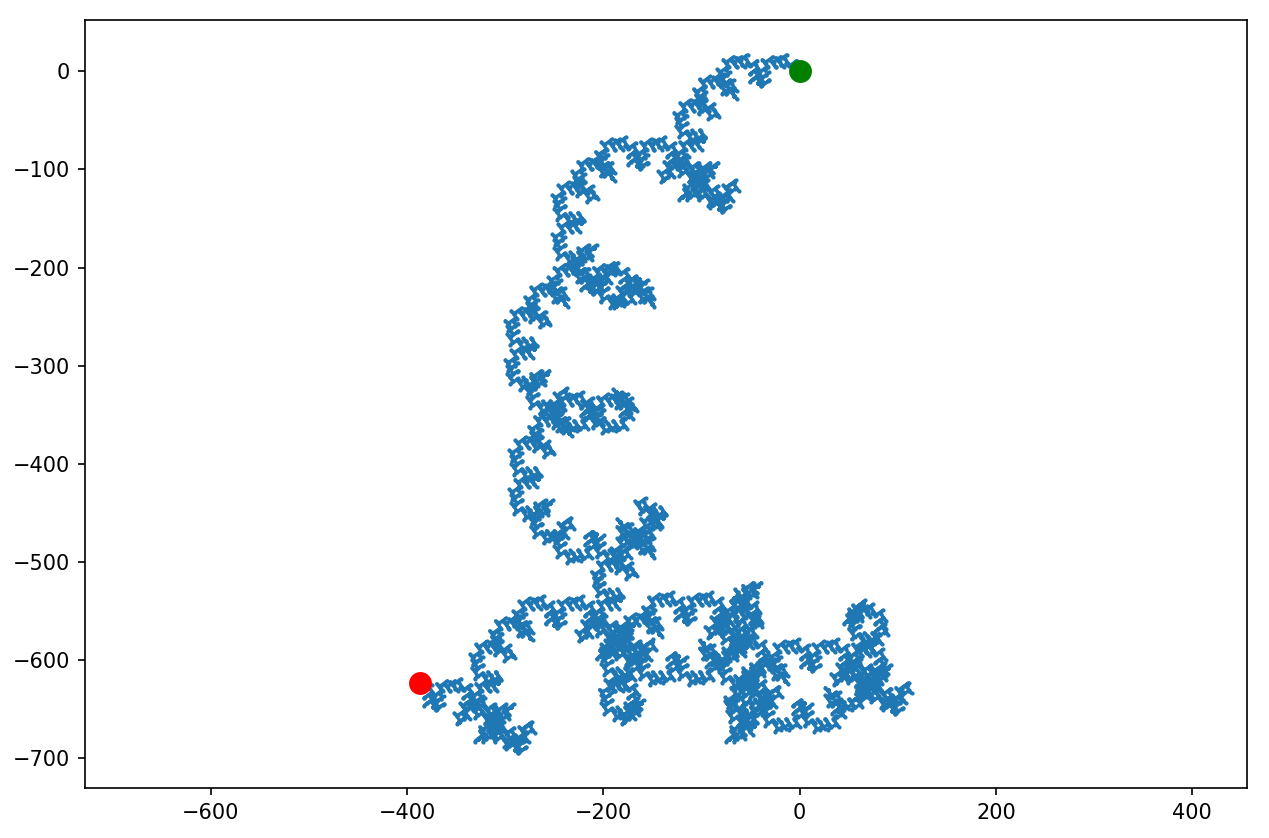
Jak widać szóstka jest zdecydowanie warta grzechu. Podbijamy więc po raz kolejny x100:

denom = 6
step_limit = 100_000_000

Efekt:

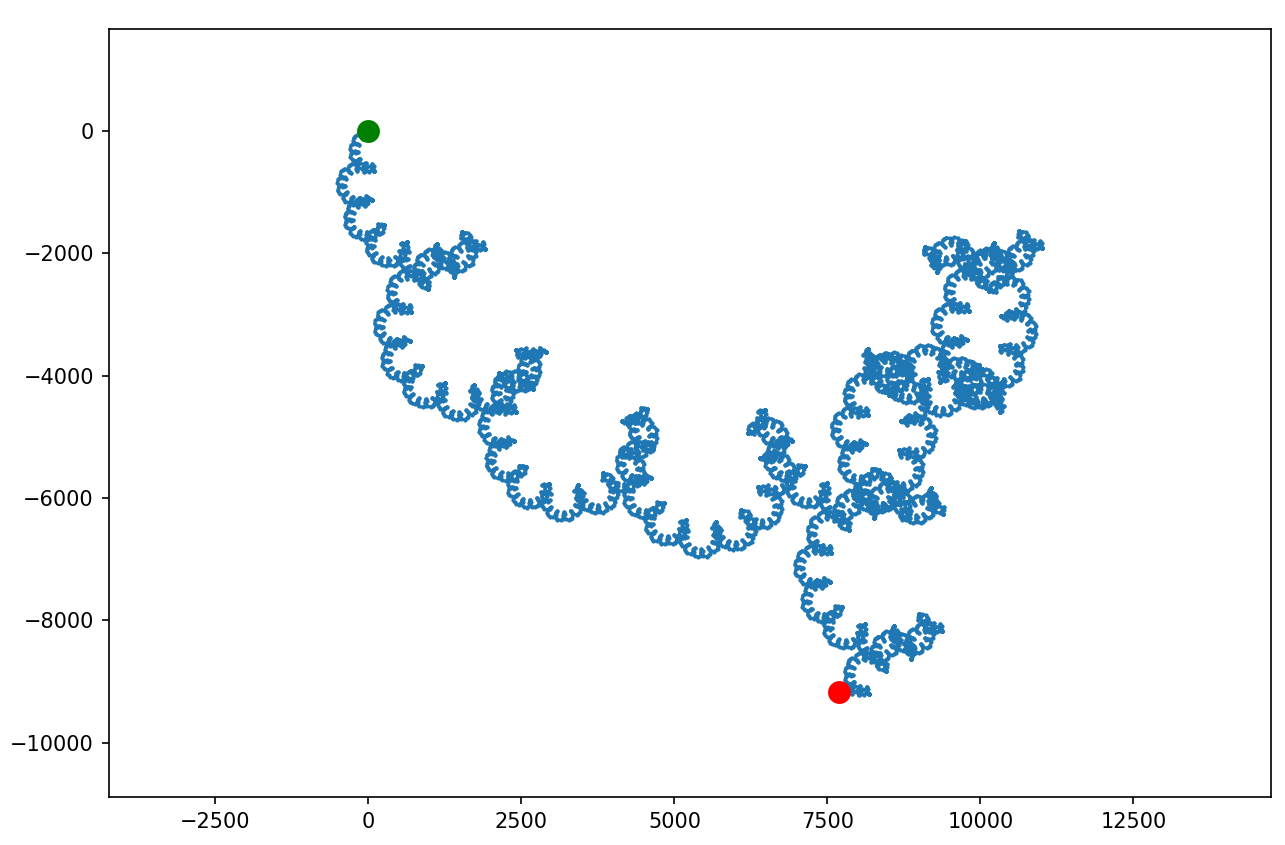
Ósemka jest nudna, natomiast dziewiątka wygląda tak:

1000 kroków:

Sto tysięcy:

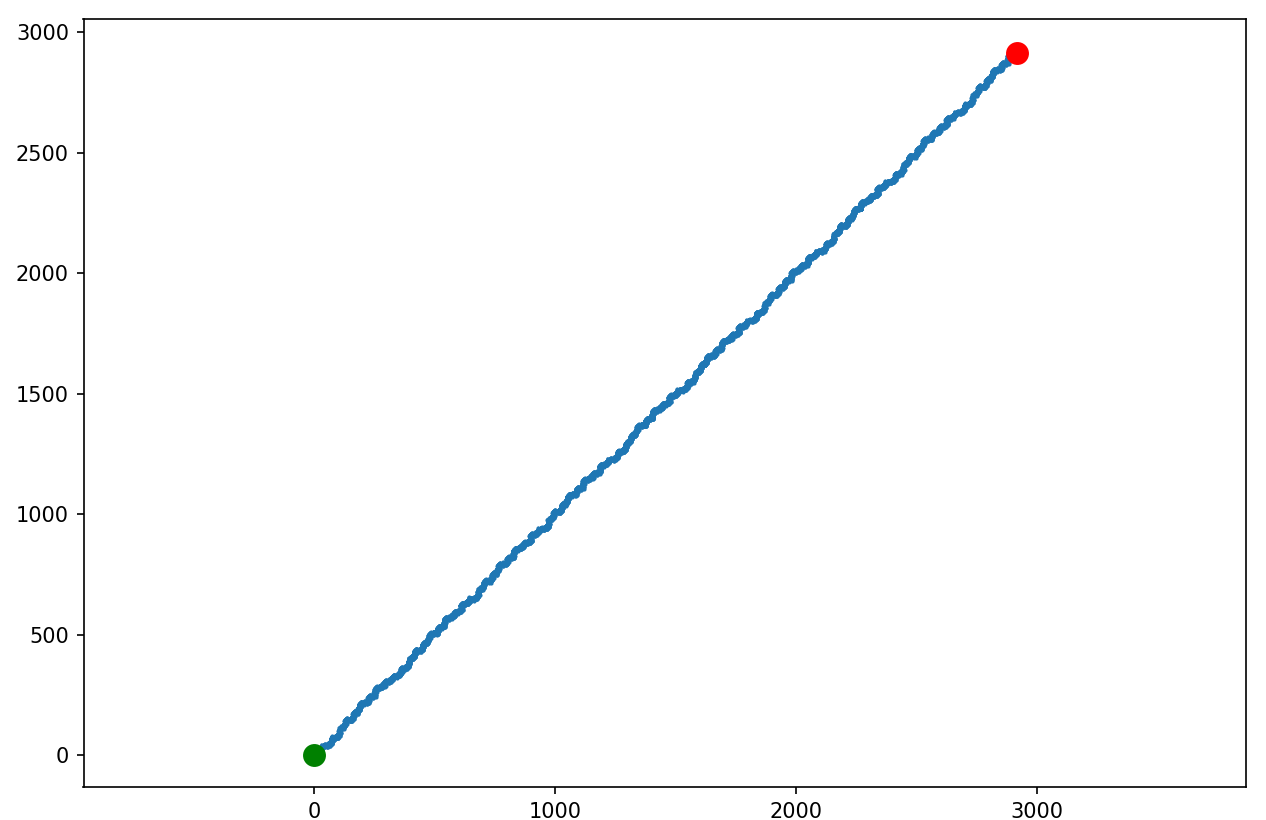
Nuda. Ale zaryzykujemy jeszcze podbicie do miliona:

Bez zmian, odpuszczamy.

A co jeżeli wskoczymy w podzielniki dwucyfrowe? Tu dynamika robi się całkiem ciekawa, bo szukamy wystąpień dwóch cyfr obok siebie, a nie tylko jednej. Zacznijmy od 10:

100 tysięcy kroków:

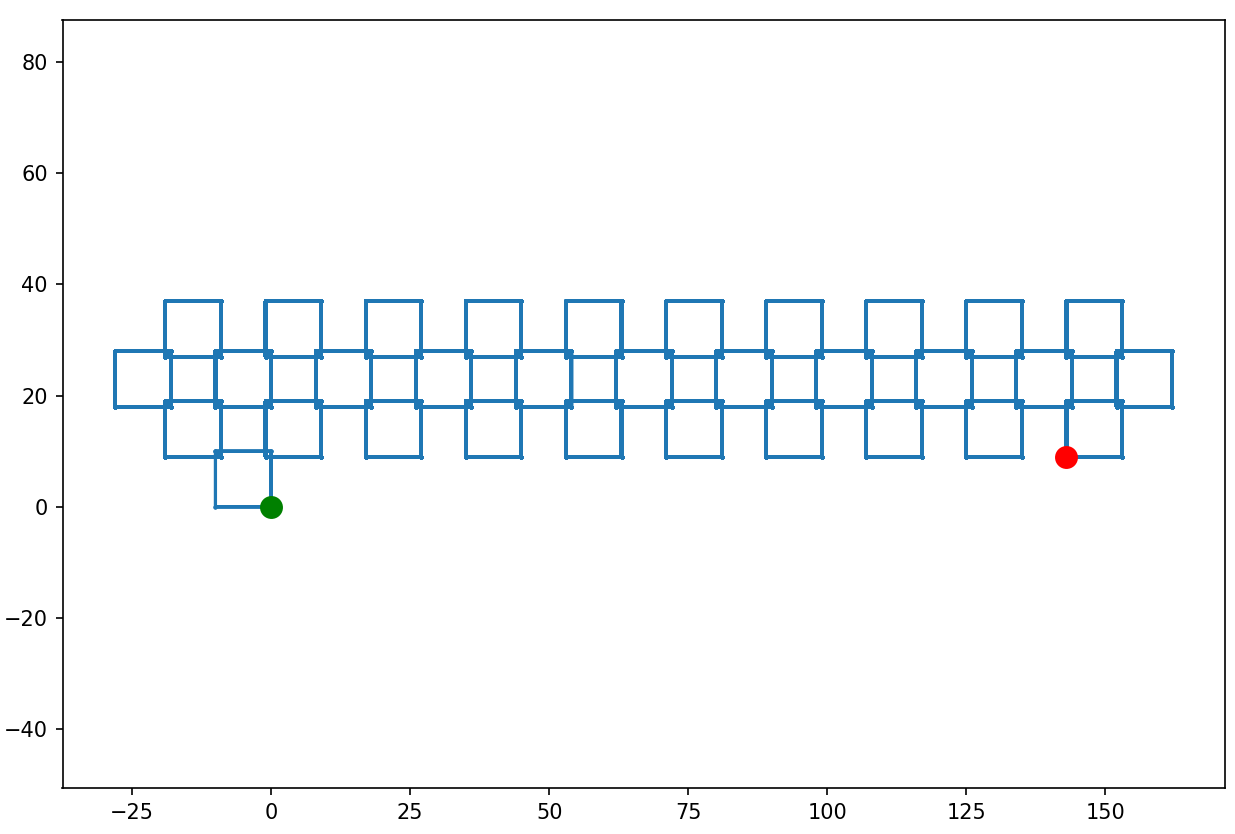
Niby nudno, ale nie do końca. Sprawdźmy dla miliona:

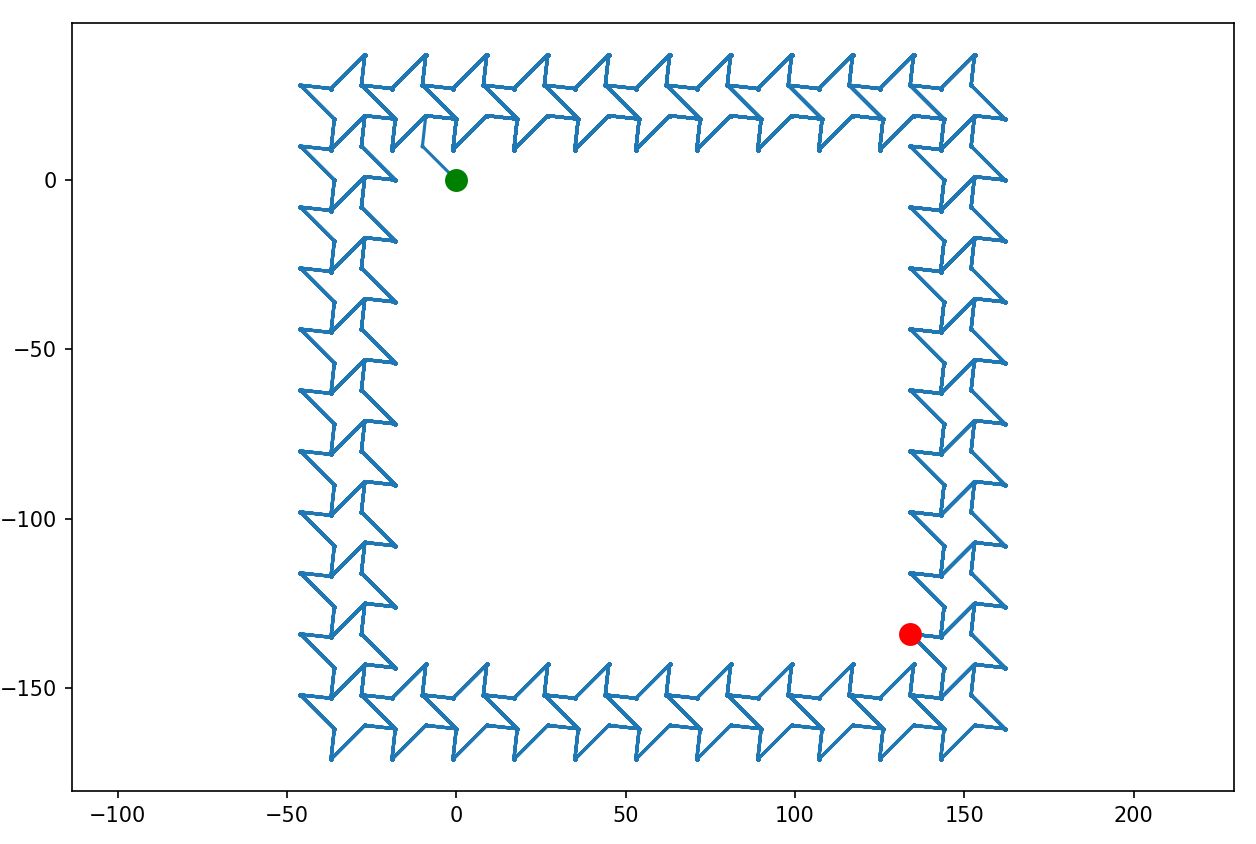
Ładnie! Zwiększamy do 100M:

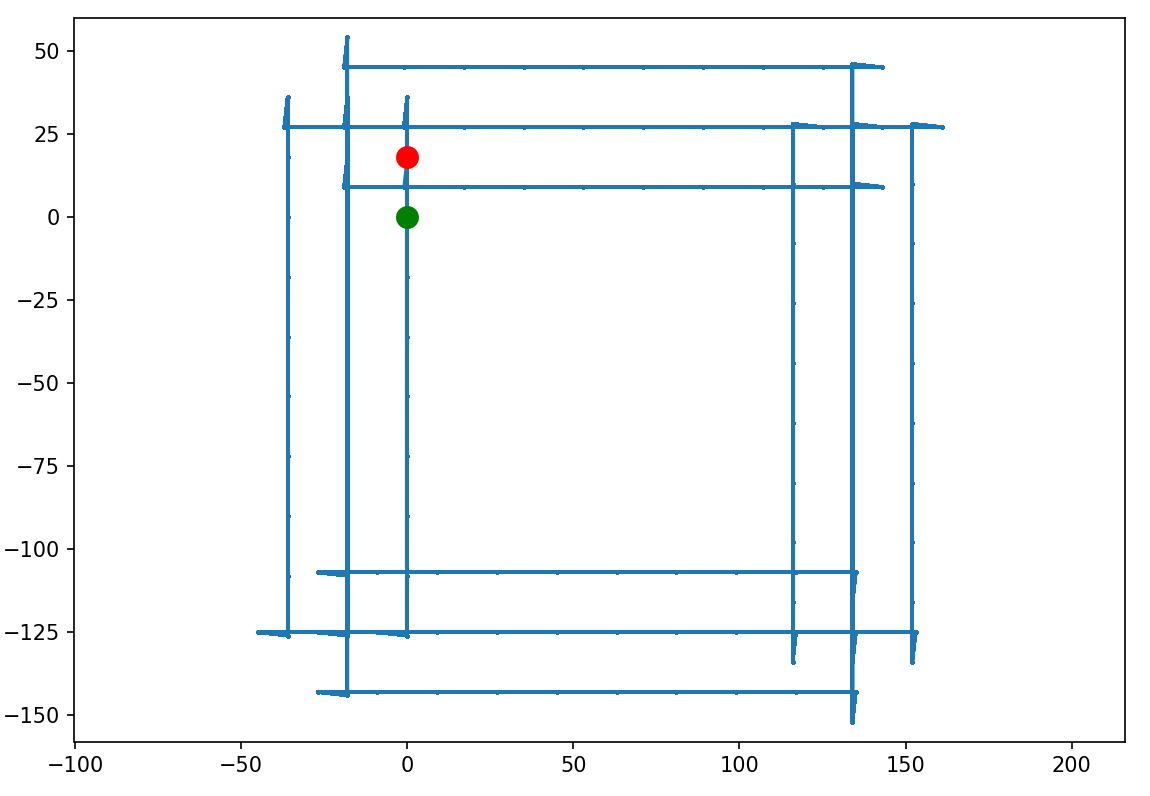
Chyba się zapętliło, nie sprawdzam dalej.

Dalsze eksperymenty wykazują, że najciekawsze wzorki uzyskuje się (na ogół) w dwóch przypadkach:

1. Kiedy liczba w mianowniku jest iloczynem dwóch liczb pierwszych (choć są wyjątki, np 10 powyżej)
2. Kiedy liczba w mianowniku jest "mocno złożona", czyli ma dużo małych podzielników pierwszych, na przykład 24 czy 48.

24, 10M kroków:

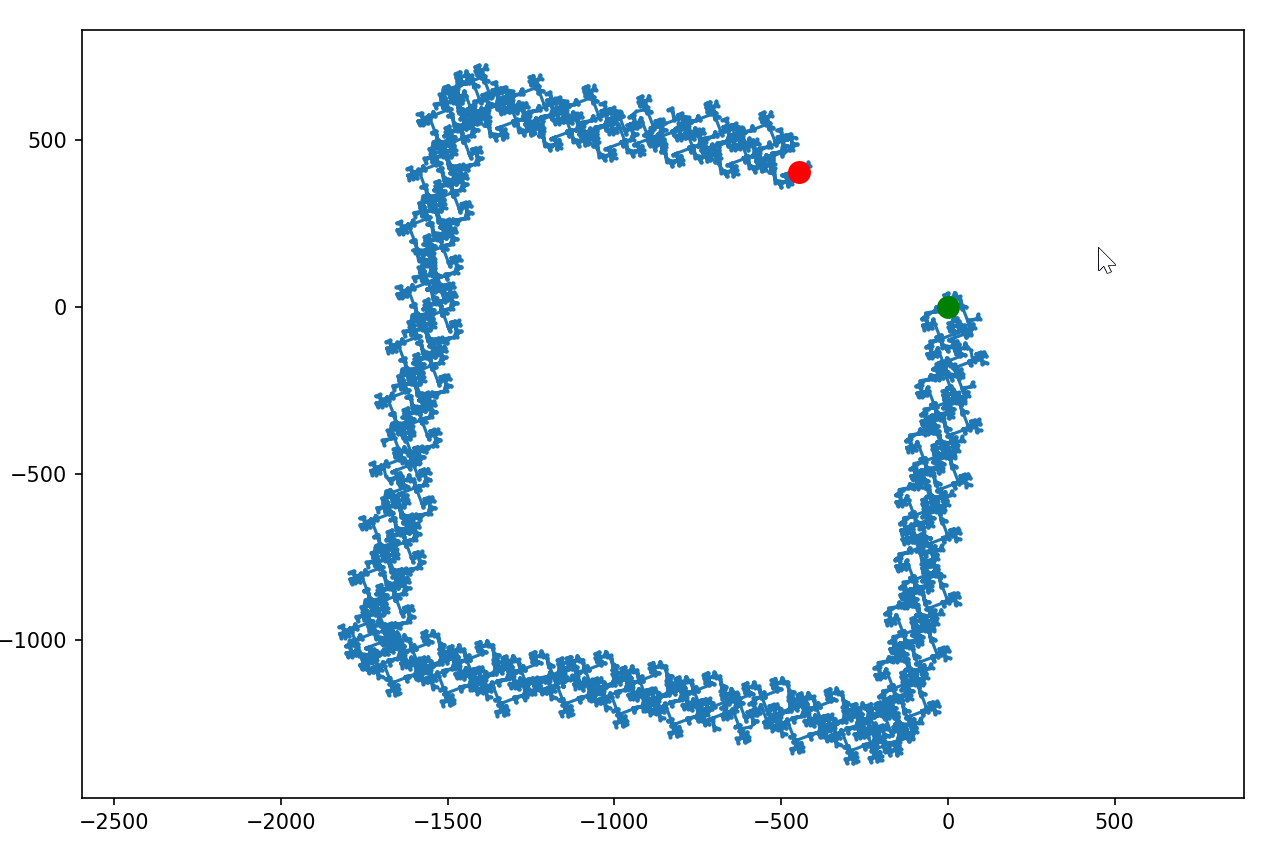
48, 1M kroków:

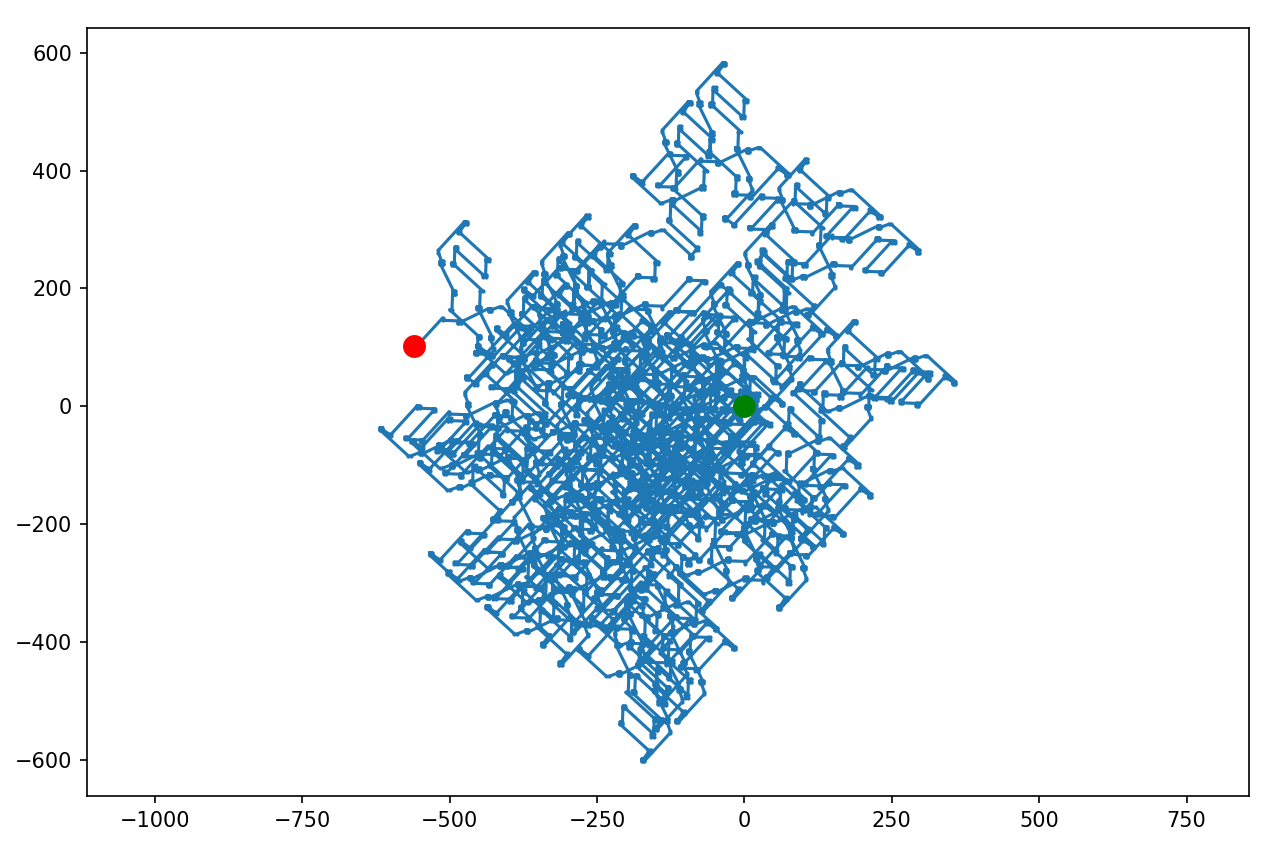
Najlepiej jednak po prostu eksperymentować z różnymi liczbami kroków i podzielnikami - wygląda na to, że proces jest po prostu chaotyczny i nieprzewidywalny.

37, 1M kroków:

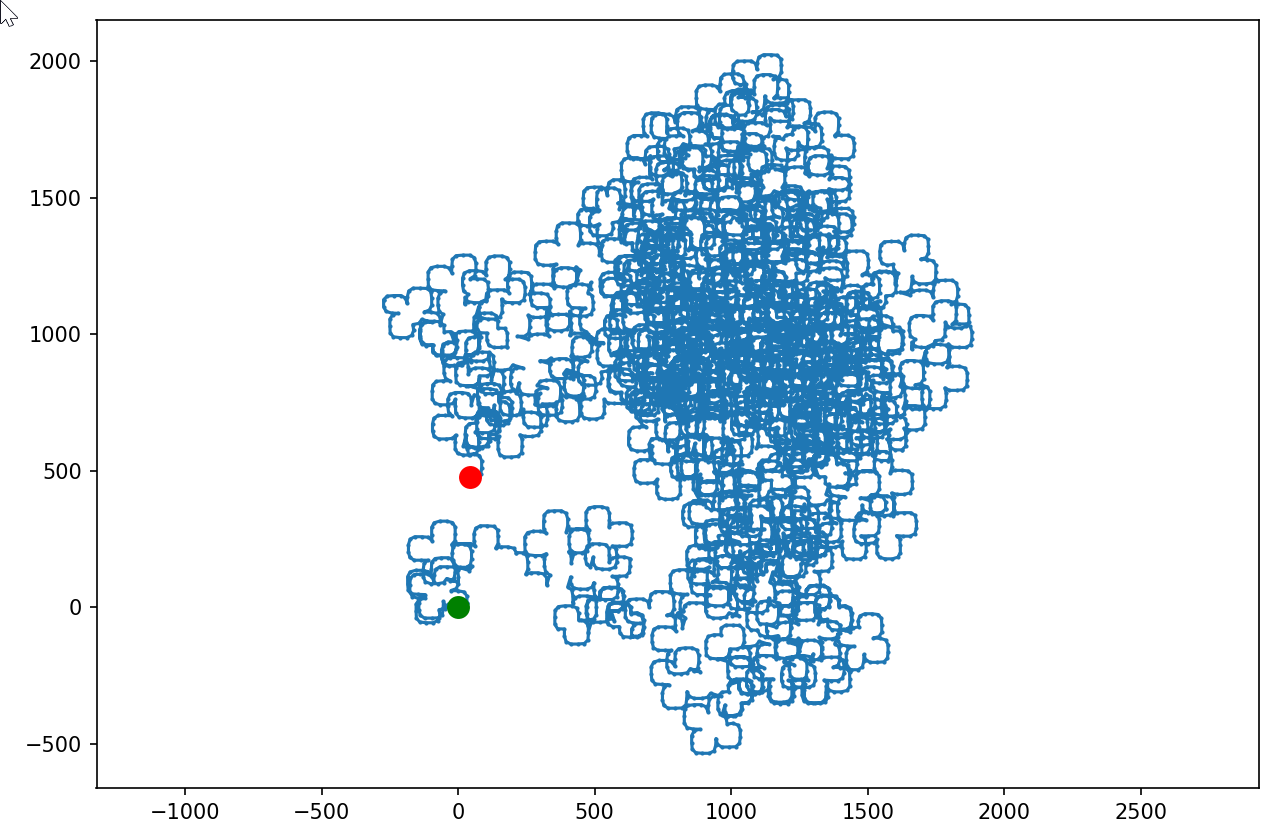
125, 1M kroków:

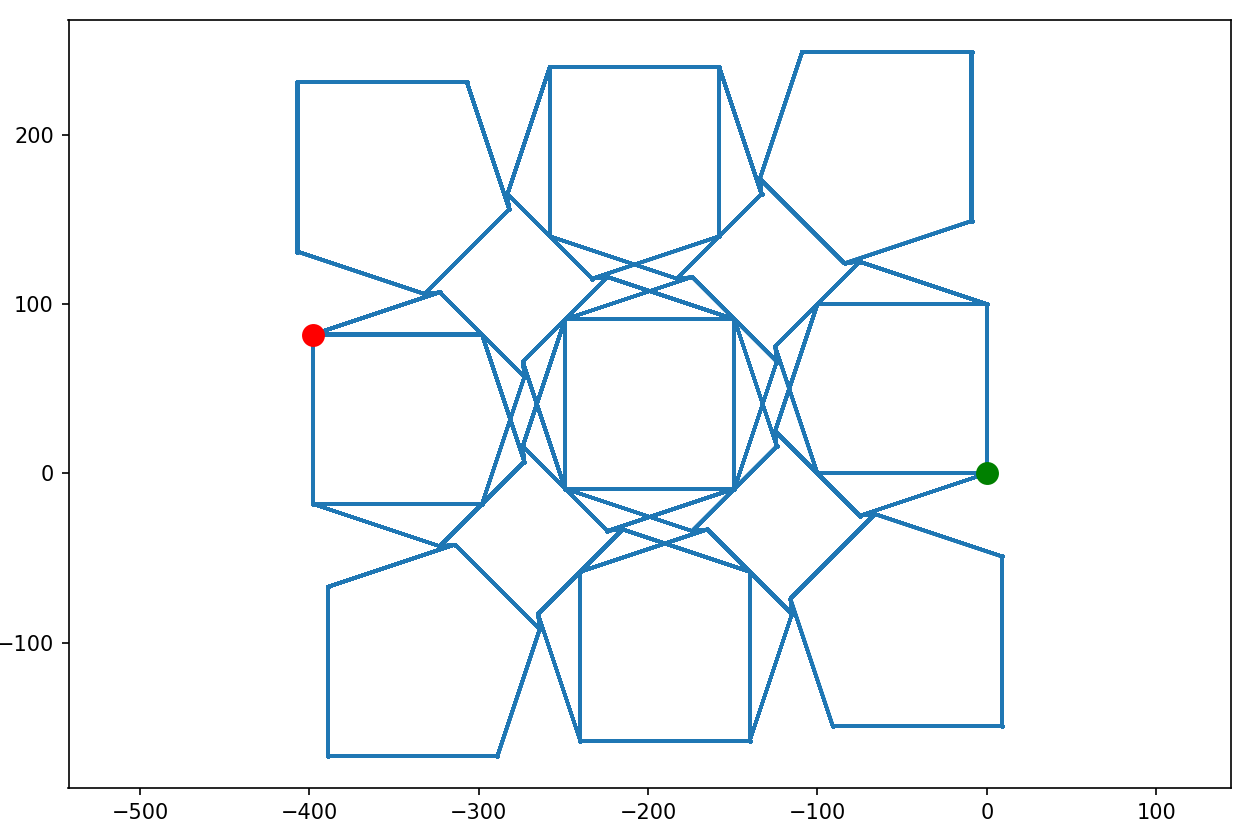
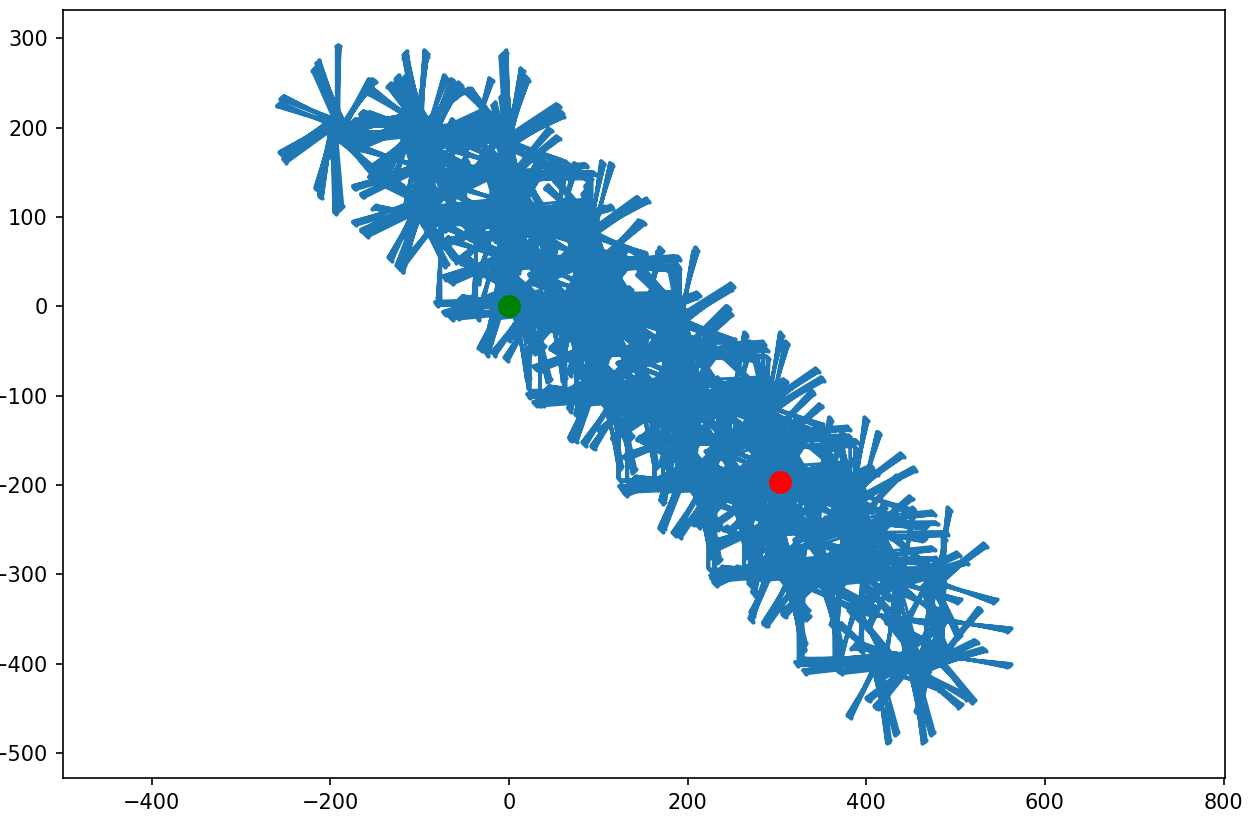
99, 1M:

To samo, zoom na okolice czerwonej kropki:

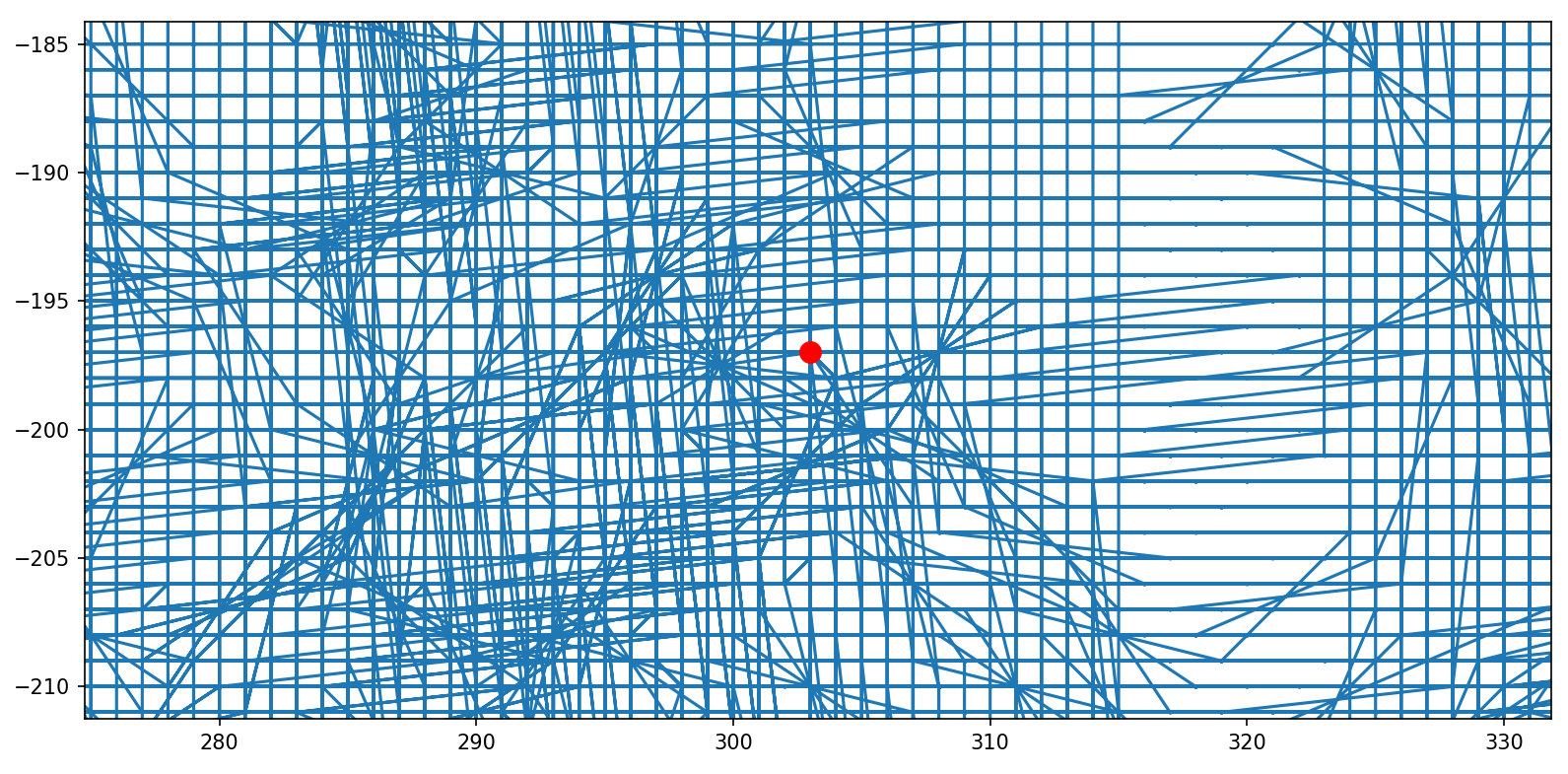
I tak dalej, i tak dalej.

Nudno, prawda?

https://xpil.eu/RQoRc 📋