Łańcuchy Markowa

https://xpil.eu/QyWKT 📋

Андрей Андреевич Марков był profesorem matematyki uniwersytetu w Leningr... tfu, Petersburgu. Żył na przełomie XIX i XX wieku. Spośród kilku niebanalnych dokonań w teorii prawdopodobieństwa na szczególną uwagę zasługuje analiza pewnej klasy procesów stochastycznych, nazwanych później procesami Markowa.

Bez wchodzenia w szczegóły, zanim przystąpię do ciekawszej części dzisiejszego wpisu, dodam jeszcze, że tytułowym łańcuchem Markowa nazywamy proces Markowa z czasem dyskretnym.

"Czas dyskretny" nie oznacza tutaj czasu, który nie wygada się przed żoną, że zamiast grać z sąsiadem w szachy łoiliśmy z nim wódę (żona zresztą nie jest głupia, skoro nie śmierdzimy szachami tylko wódą...). Przymiotnik "dyskretny" oznacza tutaj ni mniej ni więcej jak "nieciągły".

Interesującym przykładem procesów Markowa jest spacer losowy. Wyobraźmy sobie, że startujemy z punktu Zero, następnie rzucamy monetą. Jak wypadnie orzeł, skręcamy w lewo o 90 stopni. Jak reszka - w prawo (też o 90 stopni). Następnie rzucamy kostką do gry i idziemy naprzód tyle kroków, ile wypadło na kostce. Pytanie: dokąd dojdziemy po tysiącu rzutów?

A co jeżeli zamiast skręcać o kąt prosty dopuścimy możliwość losowania nie tylko ilości kroków, ale też kąta, o który należy skręcić?

A co jeżeli zamiast kostki sześciennej użyjemy dodekaedru z cyframi od minus sześć do sześć (bez zera)?

I tak dalej.

Spróbuję dziś pokazać, mniej więcej, jak to wygląda w praktyce.

W pierwszym porywie zamierzałem posłużyć się Pythonem, ale ponieważ nie znam za bardzo żadnej biblioteki graficznej, a także, ponieważ jestem leniwy, poszedłem na skróty i zobrazowałem zagadnienie w Excelu. Excel ma bowiem wykresy typu X-Y, a więc podajemy mu listę współrzędnych, a on zrobi resztę, czyli wrzuci te współrzędne w postaci punktów na wykres, przeskaluje wykres jak trzeba, a jak go ładnie poprosimy, połączy punkty linią.

Zaczniemy od symulacji spaceru losowego, w którym kąty są losowane spośród czterech z góry zadanych wartości, a długości kroków są liczbami całkowitymi wylosowanymi z zadanego przedziału.

Jak widać na załączonym obrazku, w pierwszym przykładzie dopuszczamy wyłącznie krok (nazwany tutaj skokiem) o długości jeden, a także cztery opcje zakrętu: w lewo o jeden stopień, w prawo o jeden stopień, albo w prawo o kąt prosty.

Kolejne kroki wyliczone (losowo) widzimy w wierszach od szóstego w dół. Zobaczmy jak to wygląda na wykresie:

Całkiem interesująco, prawda? Kąty proste generują kwadratowe kształty, jedynki sprawiają, że całość jest trochę "krzywo", a dłuższe serie bez wylosowania kąta prostego powodują dłuższe odcinki "prawie-proste", grupujące całość trasy na kilka zagęszczonych obszarów.

Spróbujmy kilka razy odświeżyć dane (F9):

Widać, że po tysiącu kroków (tyle wierszy ma tabelka zaczynająca się od wiersza nr 6) można dotrzeć w zupełnie nieprzewidywalne miejsca, po całkiem niebanalnych trajektoriach. A to dopiero początek, bo ograniczamy się wyłącznie do kątów prostych.

Zobaczmy co będzie, jak dopuścimy kąty w okolicach 45 stopni:

W efekcie dostajemy ścieżkę o podobnej charakterystyce: zakręty układają się w niepodokańczane ośmiokąty, czasem trasa się zapętli.

A teraz spróbujmy zaostrzyć nieco kąty: dopuszczamy wyłącznie zakręt o kąt 175 stopni. Jaki będzie efekt?

Po pierwsze, widać, że wyeliminowaliśmy czynnik losowy. "Losujemy" spośród czterech identycznych wartości kąta, oraz dwóch identycznych wartości kroku. W efekcie dostajemy gwiazdkę. Oczywiście różne wartości kąta dadzą różne krzywe:

(od tego miejsca włączyłem excelową opcję "wygładzania linii", efekt jest taki, że zamiast ostrych narożników mamy łagodne zawijasy, coś jakby krzywa Lissajou)

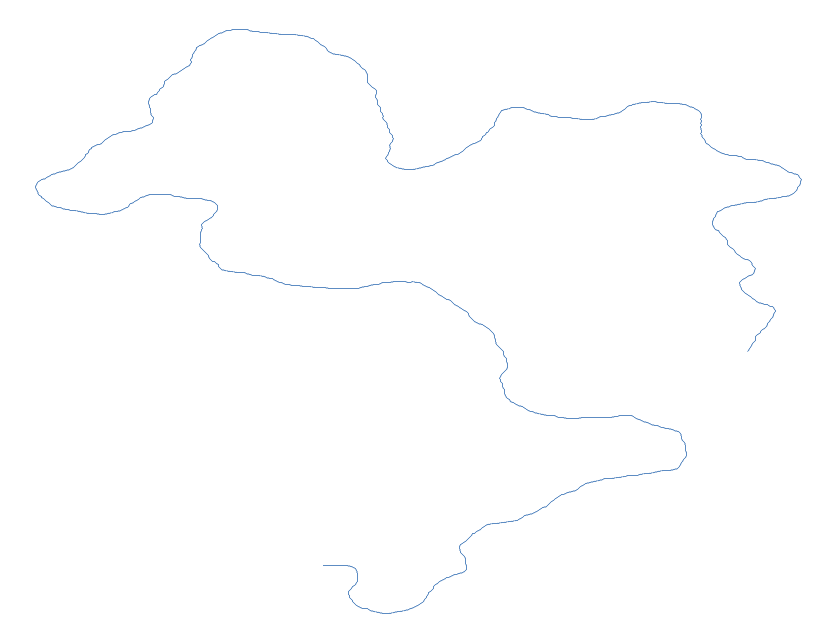
Pozostańmy jeszcze na chwilę przy deterministycznej wartości kroku i poeksperymentujmy z wielokątami foremnymi. Co będzie, jeżeli dopuścimy kąty z zakresu 71-73 stopni?

Efekt jest taki, że dostajemy trochę zabazgraną namiastkę pięciokąta foremnego. Jeżeli zmienimy zakres kątów na 89-91 stopni, dostaniemy analogiczną podobiznę kwadratu:

Oczywiście kwadratowość kwadratu będzie tym kwadratowsza, im rzadziej generator liczb losowych trafi na 89 lub 91 stopni, a im częściej będzie trafiał w pełne 90.

Z trójkątami i sześciokątami kwestia wygląda podobnie, nie będę już przynudzał. Spróbujmy teraz dodać nowy wymiar i dopuśćmy losowanie nie tylko kąta, o jaki trzeba zakręcić, ale również długości kroku. Zaczniemy od wariantu najbardziej podstawowego, a więc zakręty wyłącznie o kąt prosty (dopuszczamy 0, 90, 180 lub 270 stopni), a długość kroku jeden lub dwa. Efekt?

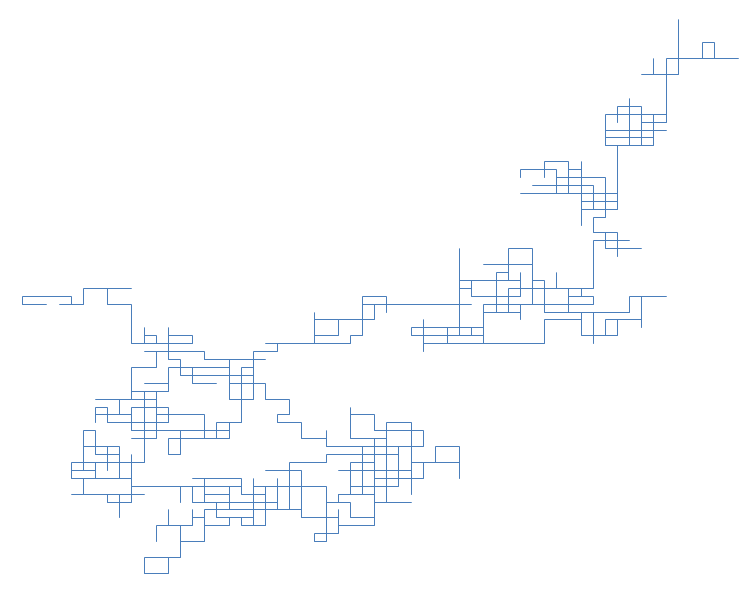
Efekt jest jakby narysować drogę bardzo niezdecydowanego niemieckiego żołnierza: chodzi wyłącznie po kątach prostych, ale nie może się zdecydować, dokąd pójść. Inne ścieżki wygenerowane tymi samymi parametrami:

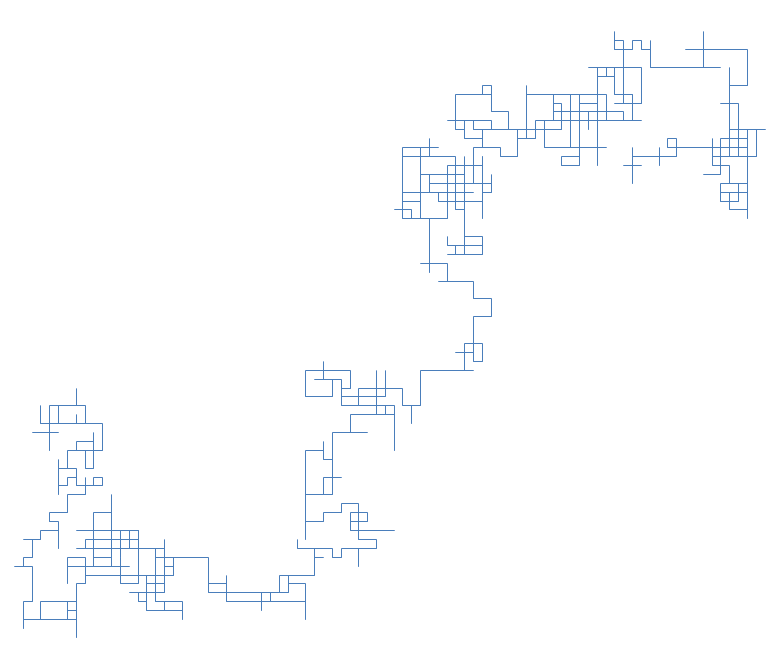
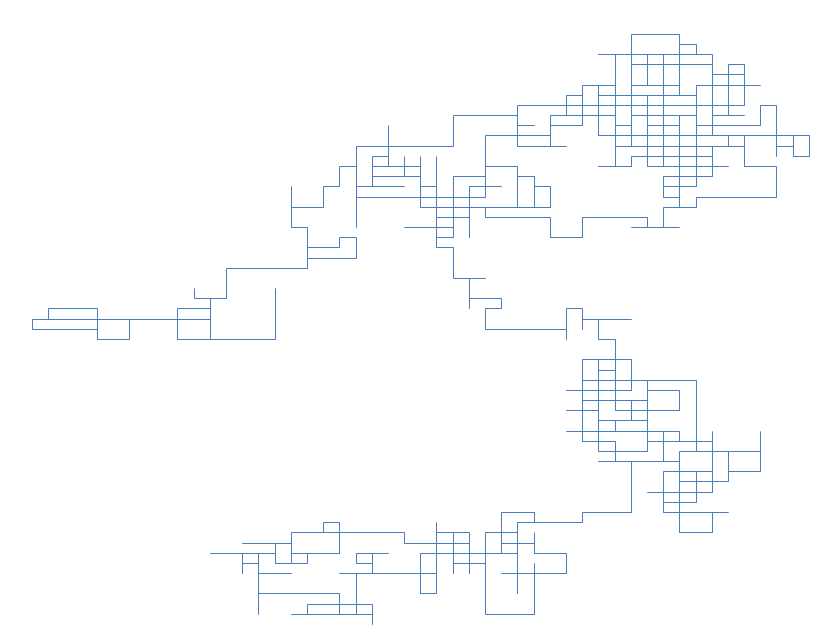
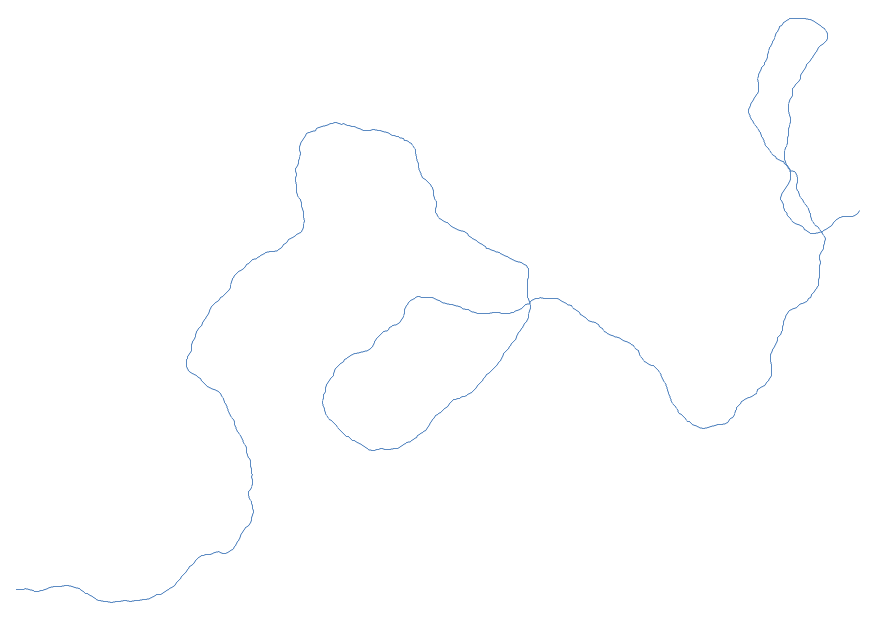
Trasa po kątach prostych jest jednak dość nudna, spróbujmy więc zobaczyć dokąd da się dojść po tysiącu kroków, zakładając niewielkie zakręty (maksymalnie 3 stopnie w każdą stronę) oraz kroki między 1 a 100:

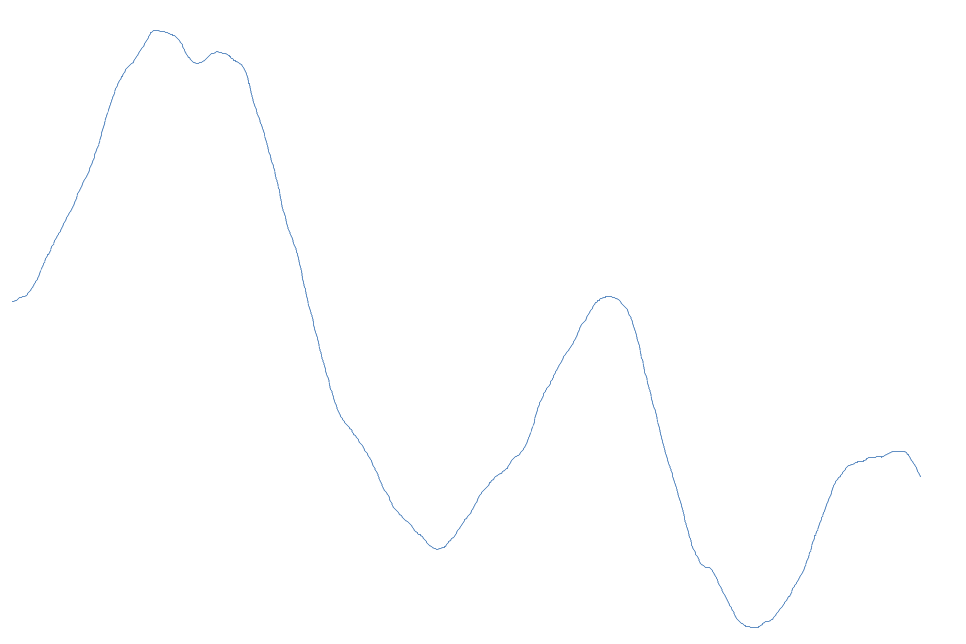
Jak widać, trasy są faktycznie łagodnie zakręcające, co do kształtu zaś, po tysiącu kroków raczej nie trafi nam się pętla, ale przy odrobinie szczęścia może uda nam się zawrócić.

A co, jeżeli dopuścimy ujemne długości kroków? W praktyce oznacza to, że możemy dać krok w tył, jeżeli na kostce wypadnie ujemna ilość oczek. Wpisujemy więc zakres kroków od -6 do 6 oraz dopuszczalne wartości kątów 2,4,5 i 8 stopni. Efekt?

Efekt jest całkiem ciekawy. Skąd się wzięły takie spiczaste zakręty? Odpowiedź jest trywialnie prosta. Jeżeli zakręcamy o, dajmy na to, trzy stopnie w lewo, a następnie dajemy pięć kroków w tył, to w rzeczywistości idziemy po takiej trasie, jakbyśmy zakręcili o 177 stopni w prawo i poszli pięć kroków naprzód. Zgadza się?

Na potwierdzenie, poniżej trasa przy nieujemnych długościach kroku (0-6), za to kątach albo bardzo niedużych (3 lub 5 stopni), albo prawie półpełnych (170 lub 175 stopni):

Jak widać, trasa wygląda podobnie do poprzedniej.

A więc tak naprawdę ujemne długości kroków podwajają nam ilość dostępnych kątów. Spróbujmy to wykorzystać:

Na ostatnim obrazku, szarą czcionką dodałem wartości tych dodatkowych czterech kątów uzyskanych poprzez zastosowanie ujemnej długości kroku. Jak widać, kształty tras są podobne jak przedtem przy trasach o "łagodnych" zakrętach, ale od czasu do czasu lekko "najeżone", jak gdyby wędrowiec nie mógł się zdecydować, czy już gnać w krzaki, czy jeszcze kawałek przejść.

Dotychczas skupiałem się na wariancie, w którym wartości kątów są losowane ze skończonego, maksymalnie czteroelementowego zbioru liczb. Tymczasem można przecież zamiast tego zastosować przedział wartości, podobnie jak zrobiliśmy to w przypadku kroku. Efekty będą podobne, ale nie identyczne. Przede wszystkim dopuszczamy większą "fluktuację zakrętów", a więc tak jakby "tracimy kontrolę" nad konkretnymi wartościami kątów. Efekty są, o, takie:

Najpierw przypadek szczególny, bez losowości: kąt zablokowany na jeden, krok tak samo. Efekt łatwy do przewidzenia:

Tyle gadaniny żeby narysować zwykłe kółko, w dodatku niezbyt okrągłe. A konkretnie - trzystasześćdziesięciokąt, który jednak z tej odległości niczym nie różni się od koła.

Oczywiście takie rysowanie koła mija się z jakimkolwiek celem (poza edukacyjnym, a i to bardzo wątpliwe), spróbujmy wprowadzić trochę losowości. Najpierw coś prostego: kąt od pięciu do ośmiu stopni, krok między jeden a cztery:

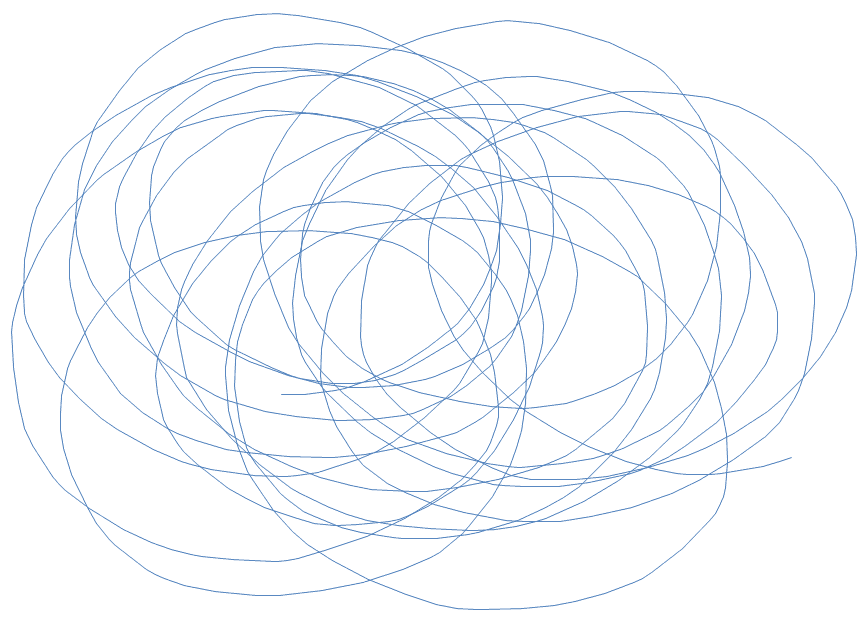
Bazgroły całkiem jakby ktoś się napruł jak szpadel ogrodniczy i próbował narysować równiutkie kółko. A co, jeżeli trochę zwiększymy zakres kątów?

Krok: 1 lub 2, kąt: od -20 do 20 stopni:

Przy takich parametrach nietrudno już o pętelkę, a przewidzieć punkt docelowy jest równie łatwo jak po trzech głębszych w lesie o trzeciej siedemnaście nad ranem.

A co jeżeli wprowadzimy znów ujemną długość kroku?

Jak widać, ścieżki tych wędrowców nadają się świetnie na projekty dla wytwórców ozdobnych drutów kolczastych. O ileż przyjemniej byłoby uciekać z więzienia przez takie malownicze konstrukcje, prawda?

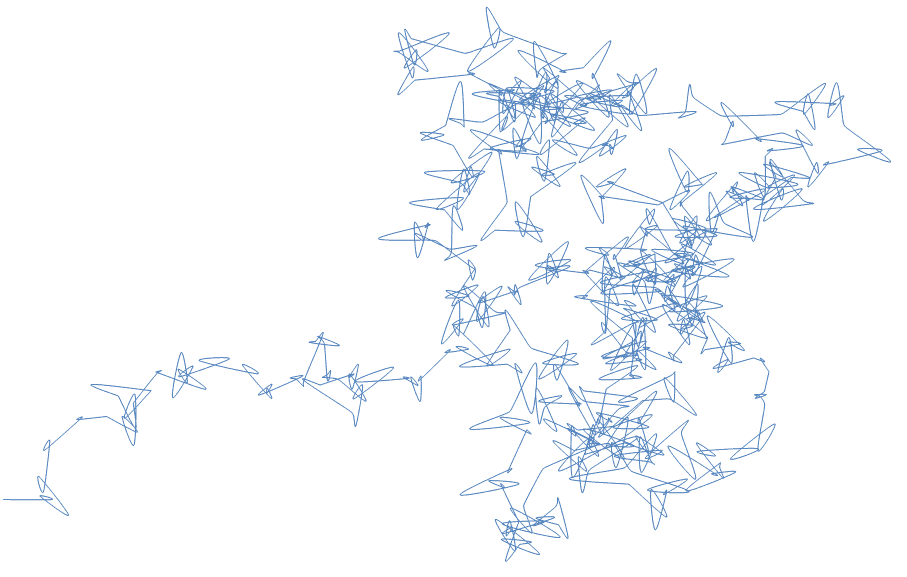
Na koniec kilka losowych tras z losowymi parametrami:

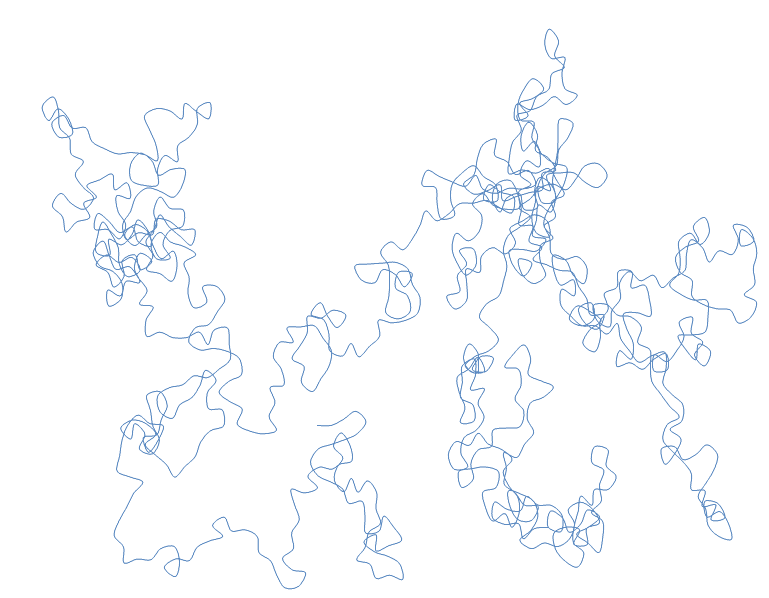
Jeżeli ktoś jest zainteresowany formułami excelowymi użytymi w tym wpisie, oto one:

Wariant 1, z zakodowanymi czterema kątami do wylosowania:

Wariant 2, z kątami losowanymi z podanego przedziału:

W ramach zabaw z Excelem i procesami losowymi, niedługo pokażę jak zasymulować prostą ruletkę (wraz z kilkoma różnymi strategiami gracza), oraz dlaczego kasyno zawsze wygrywa. Ale to już nie dziś, bo się późno zrobiło.

Czas na sen.

Dobranoc.

[yop_poll id="40"]

https://xpil.eu/QyWKT 📋