Natrafiłem niedawno w Wikipedii na Mrówkę Langdona. Pomysł jest w sumie prosty: na nieskończenie dużej planszy składającej się kwadratowych pól stoi sobie mrówka. I teraz tak: jeżeli stoi na białym polu, obraca się w lewo, a jeżeli na czarnym - w prawo. Następnie zmienia kolor pola na przeciwny (a więc z białego na czarny, lub z czarnego na biały) i przesuwa się o jedno pole do przodu. I tak do usranej śmierci.
Trochę się to kojarzy z Game of Life Johna Conwaya.
Pomyślałem sobie, że mogłoby to być całkiem niezłe ćwiczenie ogólne na posługiwanie się Pythonem.
No i się zaczęło...
Najpierw całkiem niewinna wersja minimalna:
import matplotlib.pyplot as plt
import numpy as np
dirs = {"N": [0, 1], "S": [0, -1], "W": [-1, 0], "E": [1, 0]}
L = {"N": "W", "W": "S", "S": "E", "E": "N"}
R = {"N": "E", "E": "S", "S": "W", "W": "N"}
xsize, ysize = 500,500
steps = 1000000
x, y = xsize//2, ysize//2
board = np.zeros(shape=(xsize, ysize), dtype=int)
turns = [L,R]
dir = "N"
for X in range(steps):
dir = turns[(board[x, y])][dir]
board[x, y] = 1-board[x, y]
dx, dy = dirs[dir]
x, y = (x + dx) % xsize, (y + dy) % ysize
plt.imshow(board)
plt.xticks([])
plt.yticks([])
plt.show()Powyższy kod generuje trasę spaceru Mrówki Langdona z jedną różnicą względem oryginału: zamiast nieskończonej płaszczyzny używamy prostokąta "zawiniętego" wzdłuż i w poprzek (czyli mrówka wychodząc poza lewą krawędź pojawia się po prawej stronie i tak dalej).
Wynik:

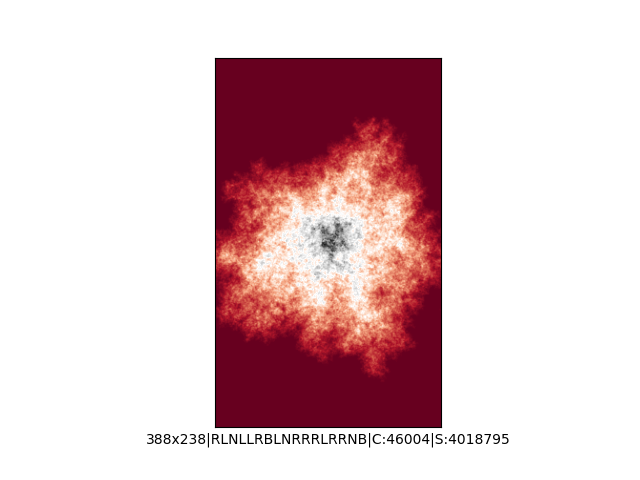
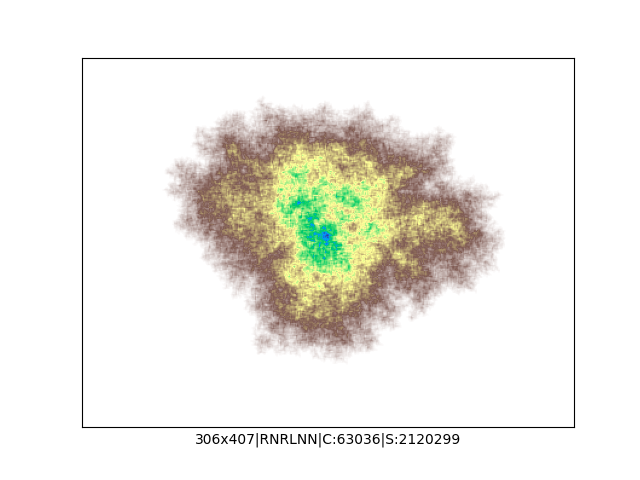
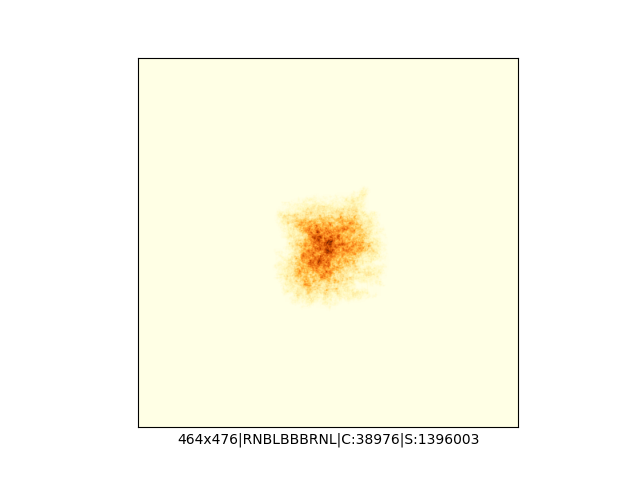
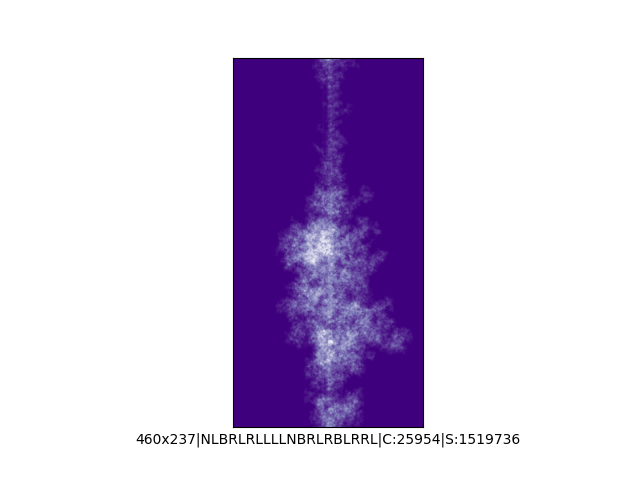
A potem spróbowałem dodać więcej kolorów, więcej opcji zakręcania, czyli do "w lewo" i "w prawo" dołożyłem opcję "zawróć" oraz "idź dalej prosto" i na koniec zrobił mi się z tego generator losowych spacerów Mrówek Langdona, którego kod wygląda teraz tak:
import matplotlib.pyplot as plt
import numpy as np
from random import choice, randrange as rr
dirs = {"N": [0, 1], "S": [0, -1], "W": [-1, 0], "E": [1, 0]}
L = {"N": "W", "W": "S", "S": "E", "E": "N"} # left
R = {"N": "E", "E": "S", "S": "W", "W": "N"} # right
N = {"N": "N", "W": "W", "S": "S", "E": "E"} # none
B = {"N": "S", "W": "E", "S": "N", "E": "W"} # back
colormaps = plt.colormaps()
for mainloop in range(1000):
xsize, ysize = 200 + rr(300), 200+rr(300)
steps, colours = 1000000 + rr(4000000), 20+rr(65515)
x, y = xsize//2, ysize//2
board = np.zeros(shape=(xsize, ysize), dtype=int)
turns = []
tt = ""
trnum = 2+rr(20)
for i in range(trnum):
t = choice(("L", "R", "N", "B"))
tt += t
turns.append({"L": L, "R": R, "N": N, "B": B}[t])
dir = "N"
for X in range(steps):
dir = turns[(board[x, y]) % len(turns)][dir]
board[x, y] = (board[x, y] + 1) % colours
dx, dy = dirs[dir]
x, y = (x + dx) % xsize, (y + dy) % ysize
plt.imshow(board, cmap=choice(colormaps))
plt.xticks([])
plt.yticks([])
xlab = "{}x{}|{}|C:{}|S:{}".format(xsize, ysize, tt, colours, steps)
plt.xlabel(xlab)
filename = "ants/langton-{}-{}-{}-{}-{}.png".format(
xsize, ysize, tt, colours, steps)
plt.savefig(filename)
print(".", end="")
print()Przed uruchomieniem skryptu należy się upewnić, że mamy lokalny folder o nazwie "ants", do którego będą trafiać wygenerowane obrazki. Skrypt wygeneruje 1000 losowych spacerów i zapisze każdy z nich w osobnym pliku png. Obrazki mają losową rozdzielczość (od 200x200 do 500x500 pikseli), losową mapę i liczbę kolorów, losowe reguły zakręcania oraz liczbę iteracji (między 1M a 5M).
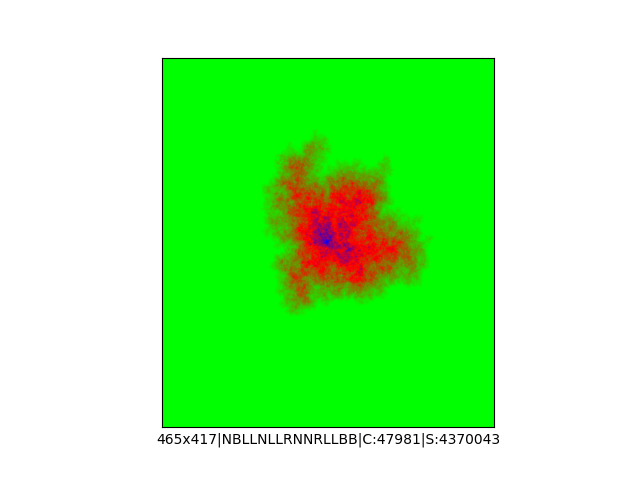
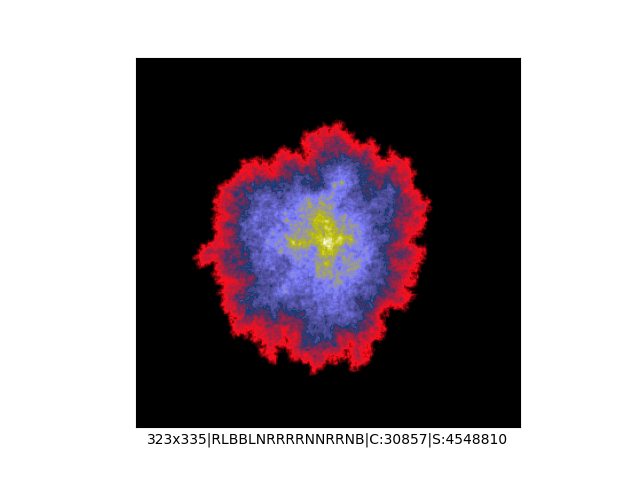
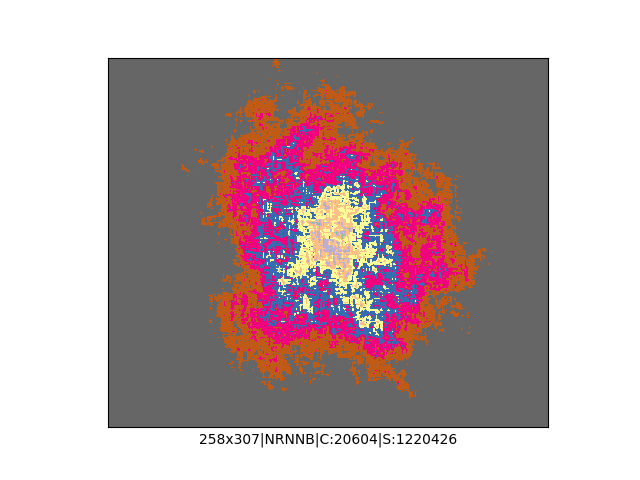
Mała próbka:

Większa próbka (kliknięcie w obrazek wyświetli go w powiększeniu):
Co dalej?
Jak czas i zdrowie pozwolą, spróbujemy pobawić się planszą heksagonalną...






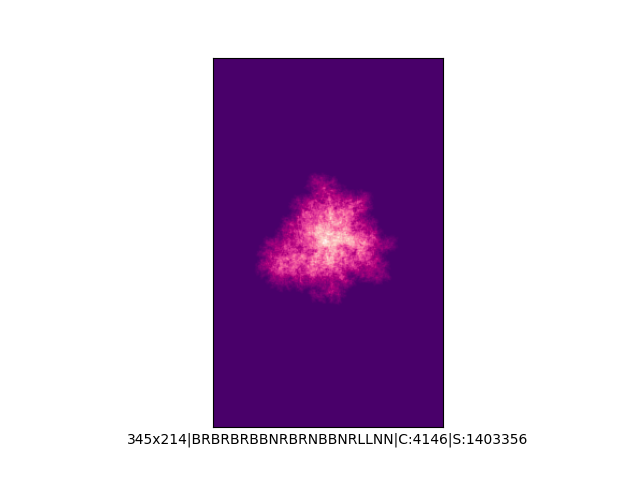









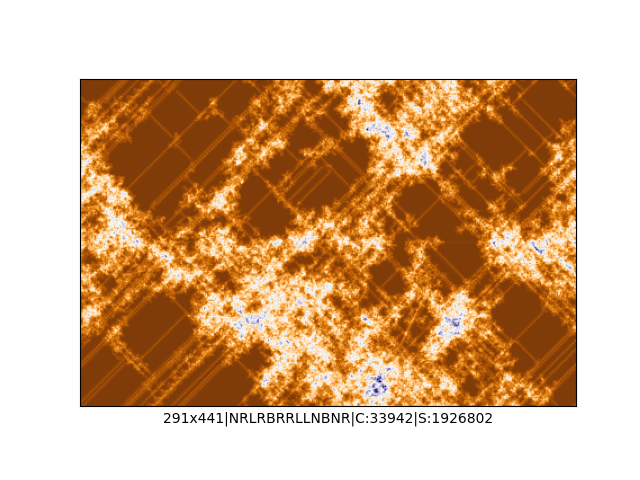

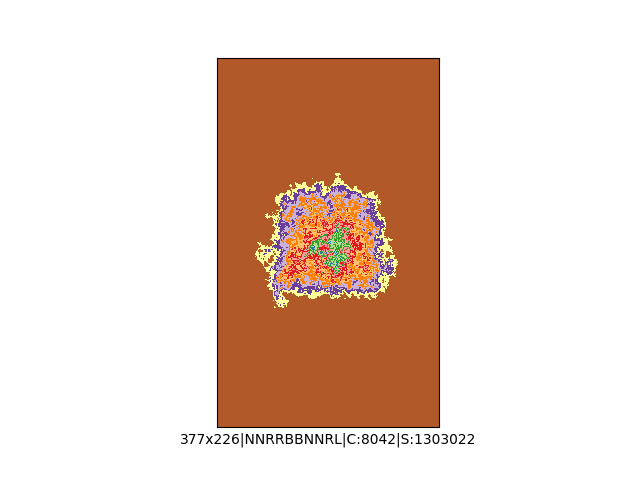








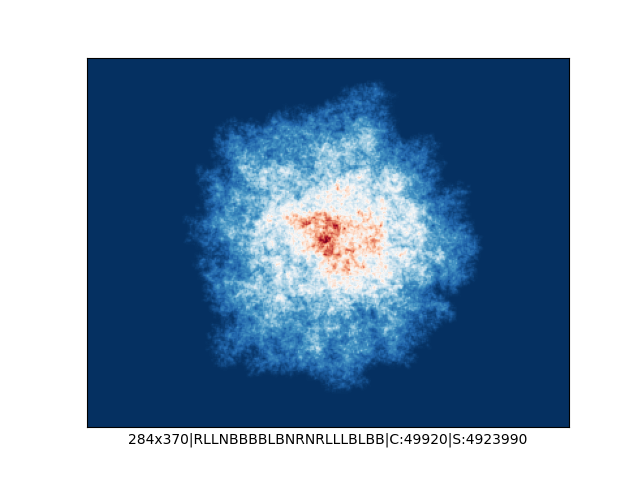
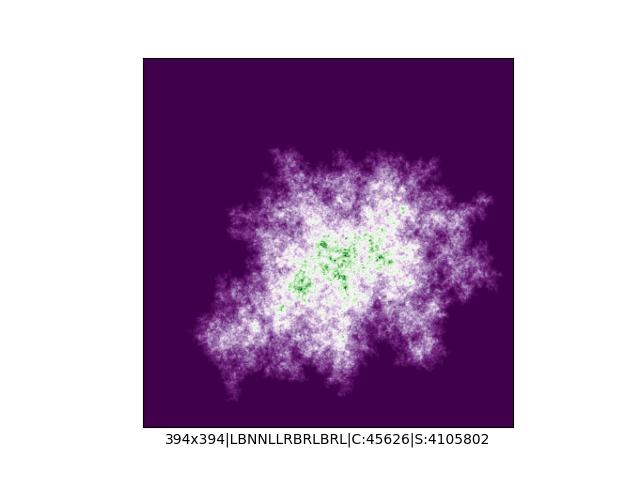














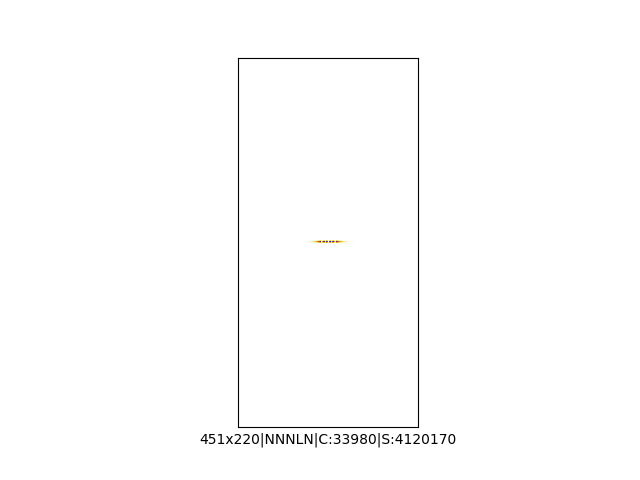
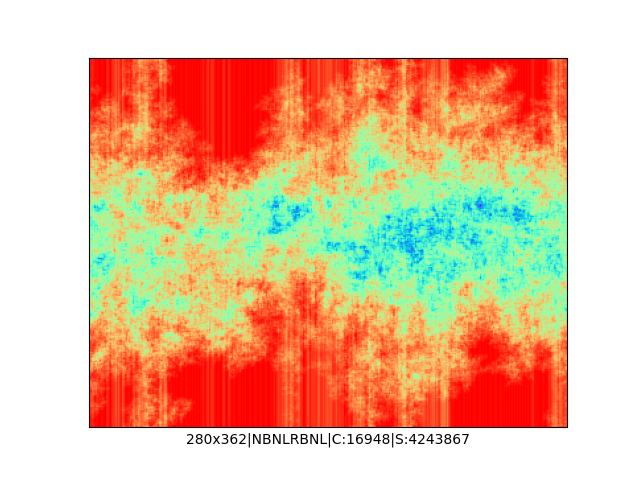

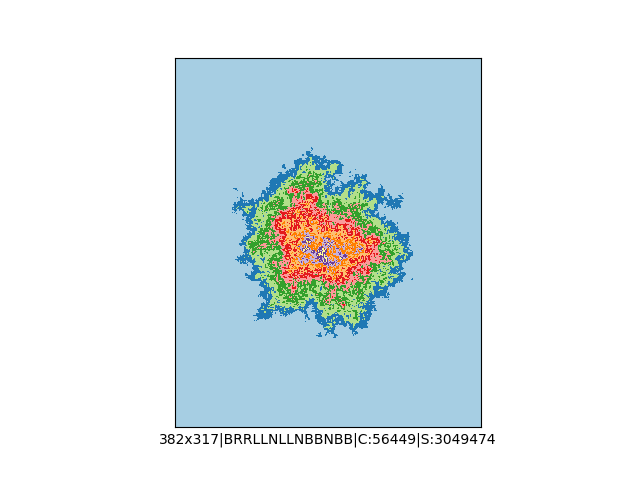
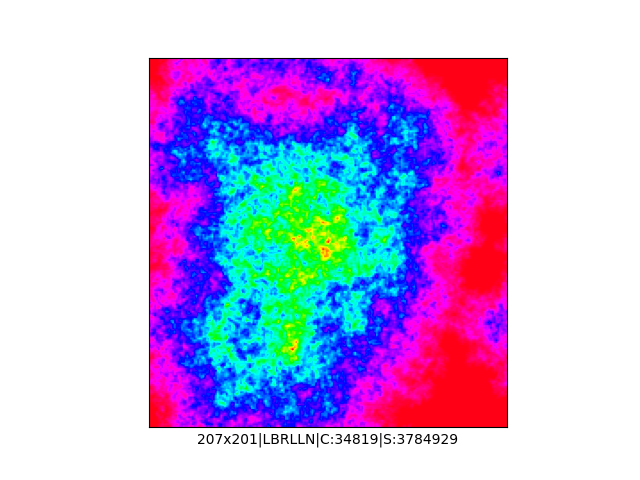




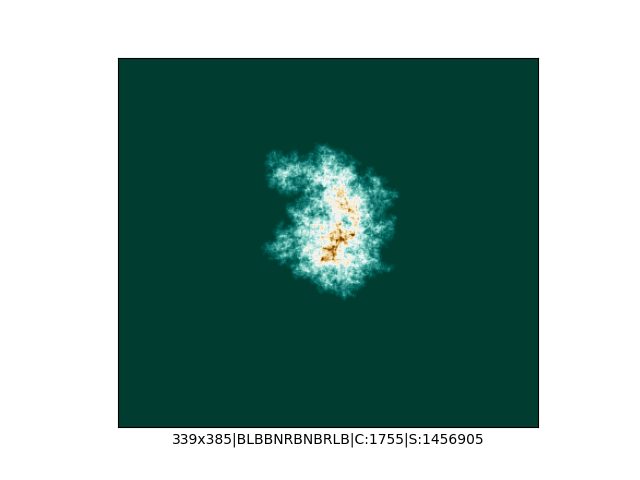




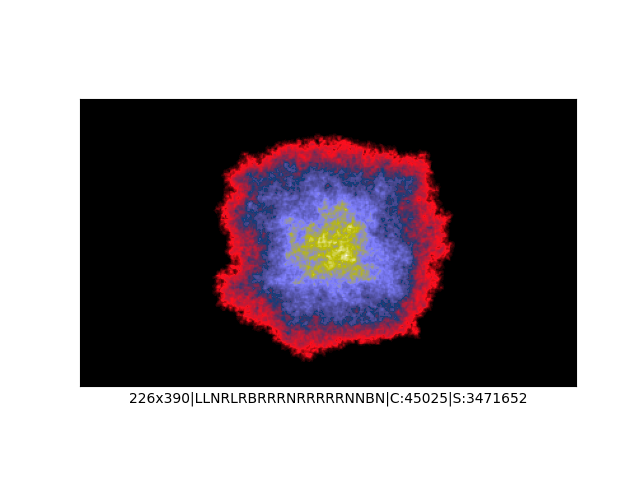











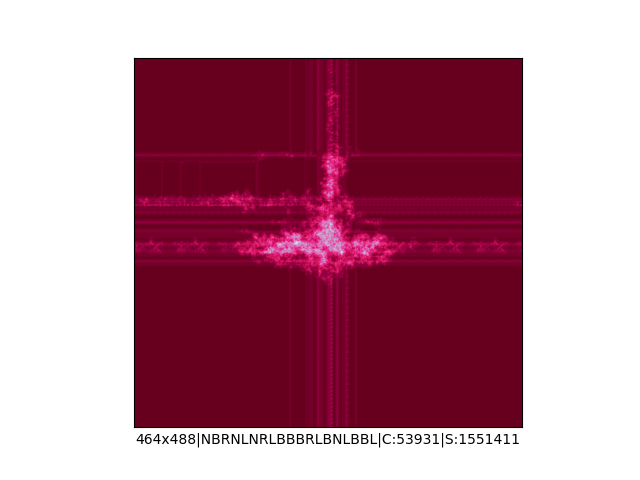
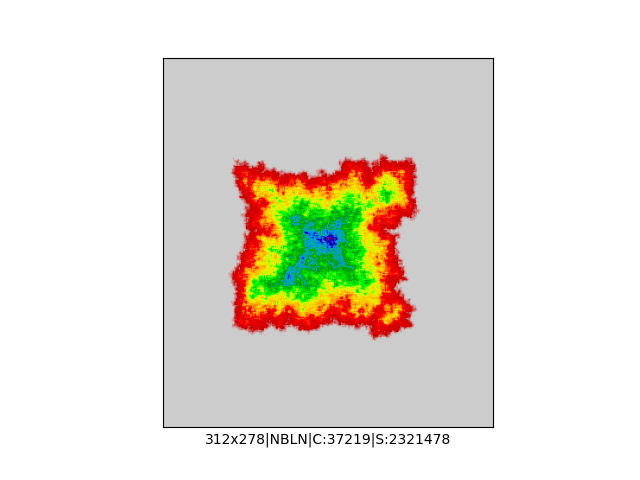


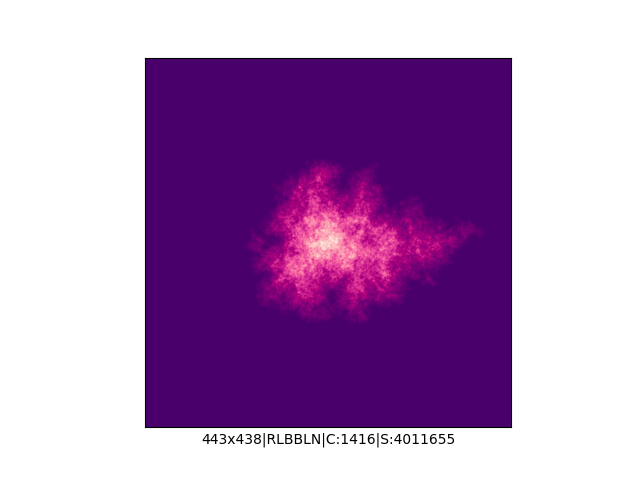






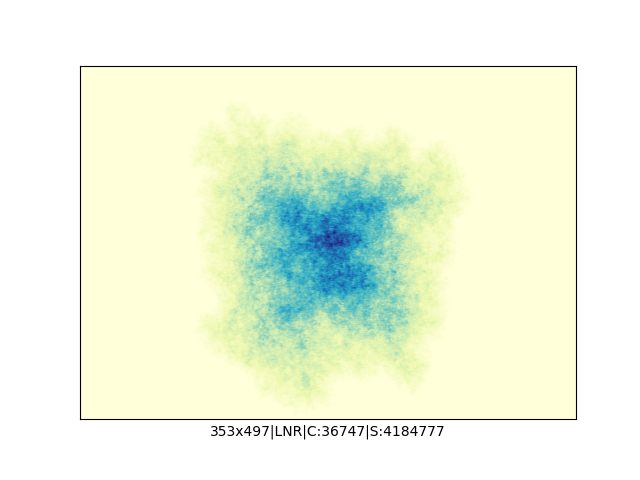










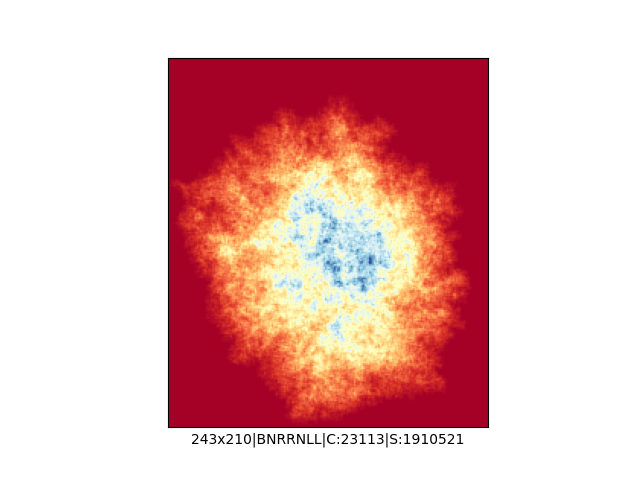


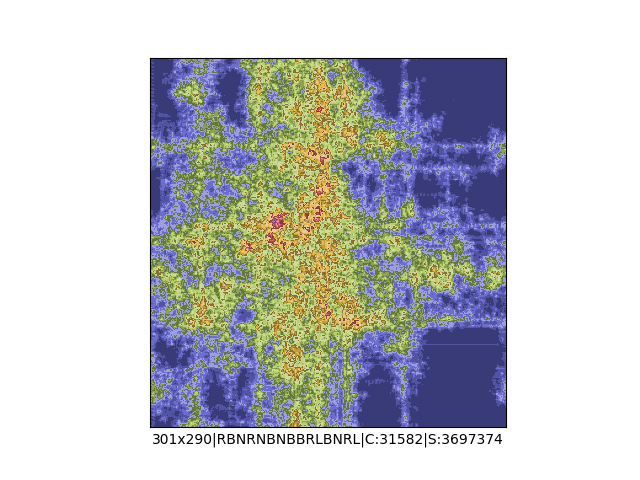






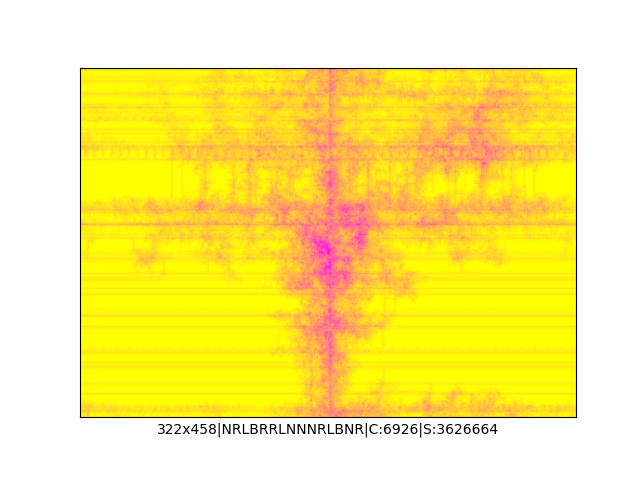





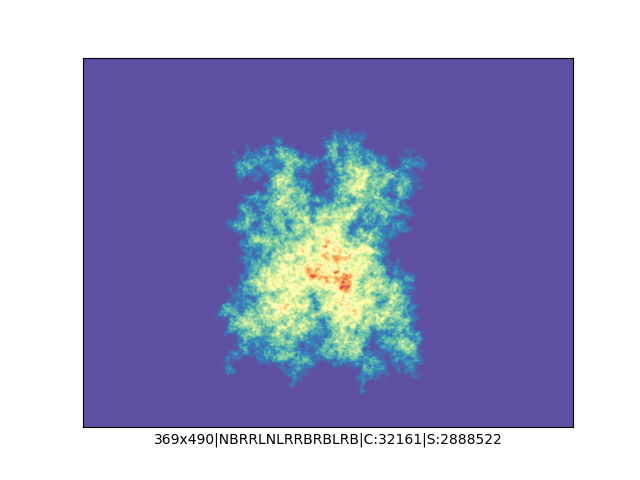

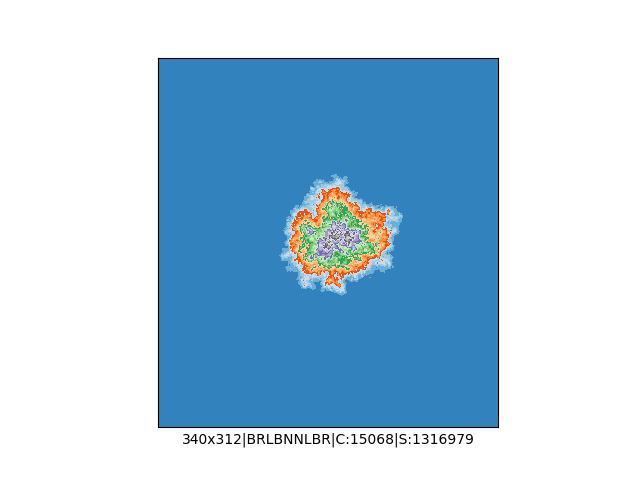




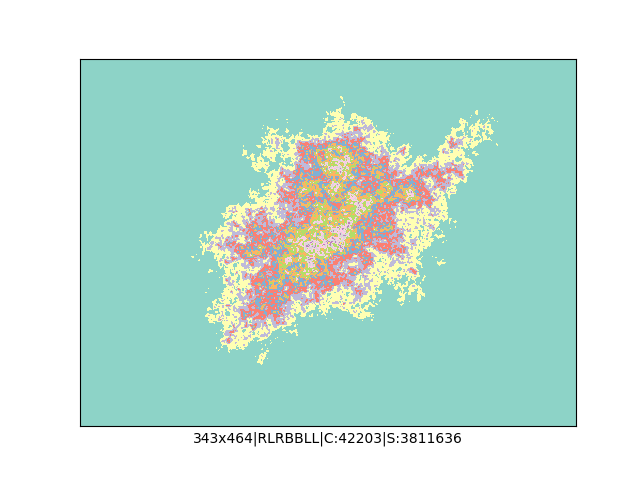





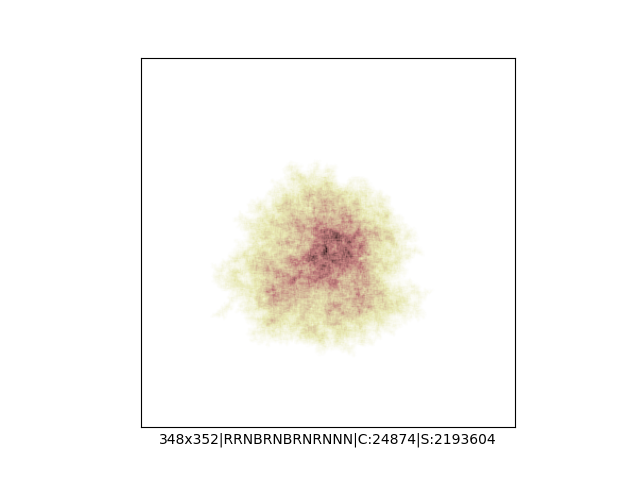

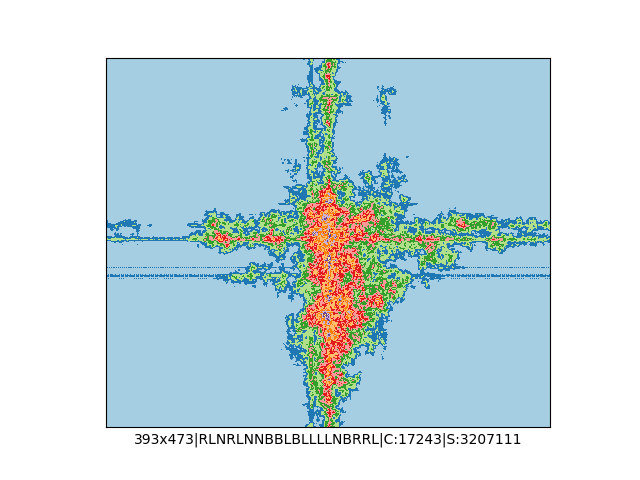



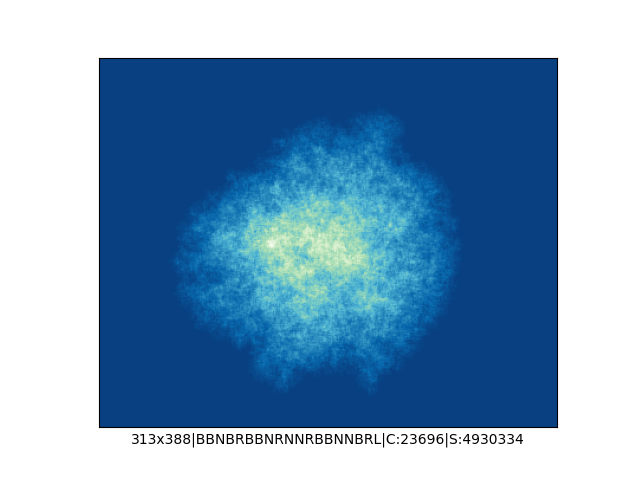





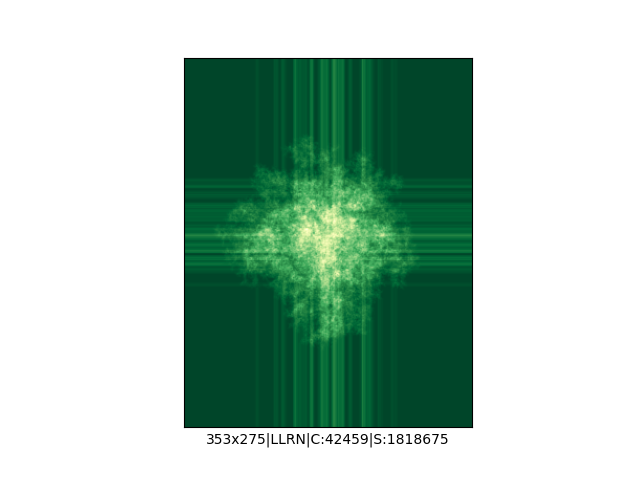
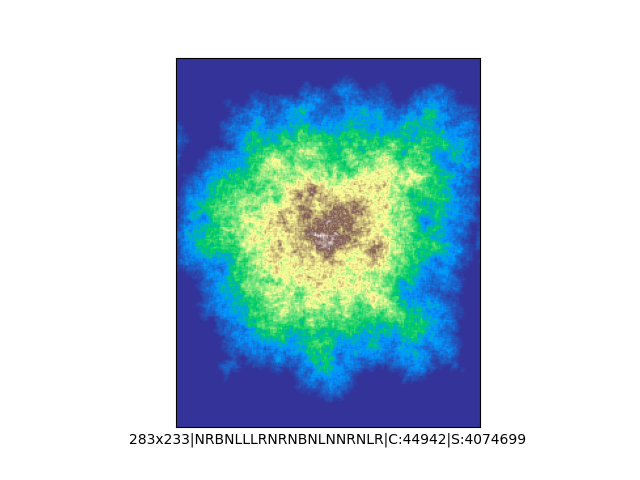







































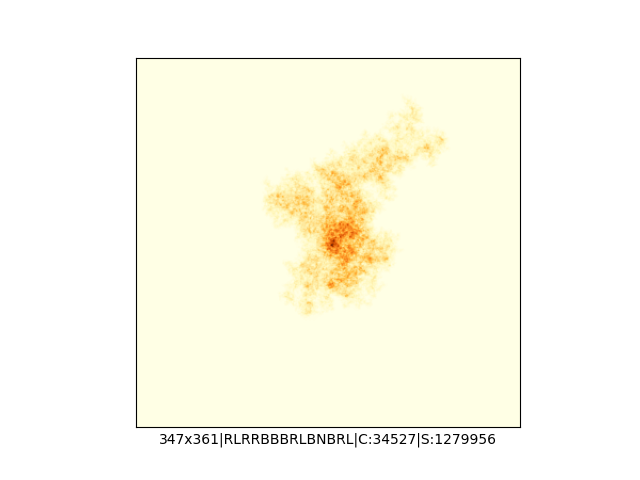

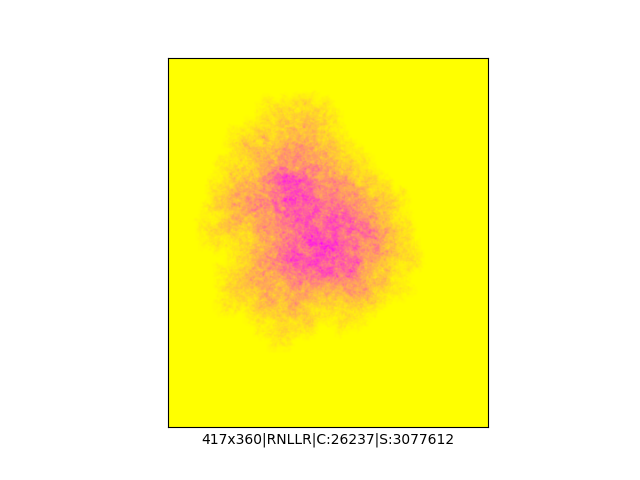











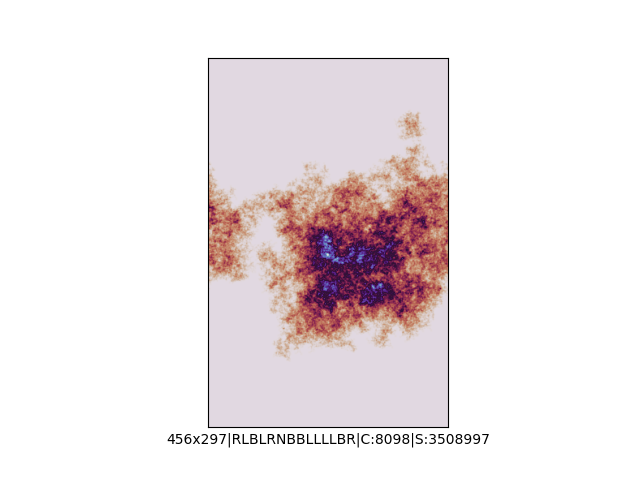
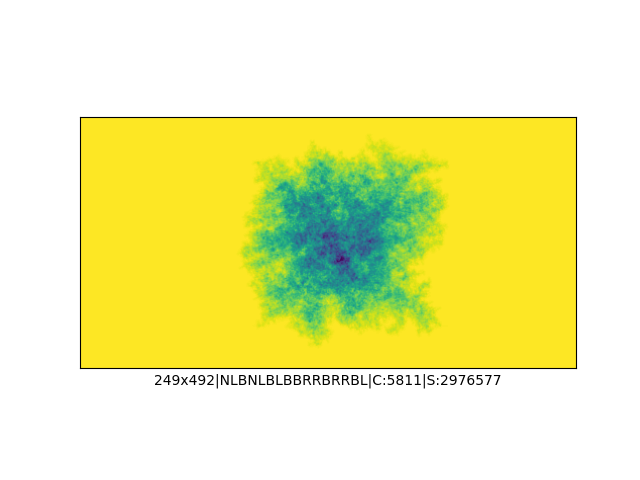



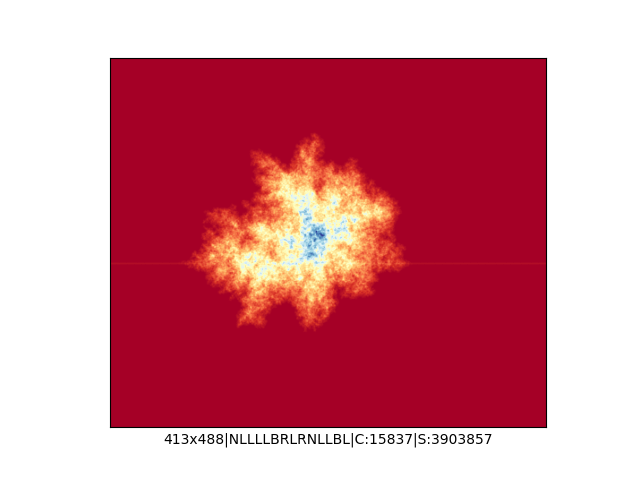

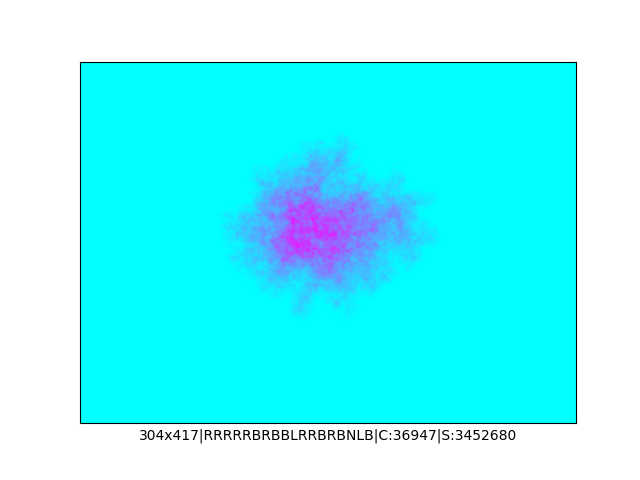



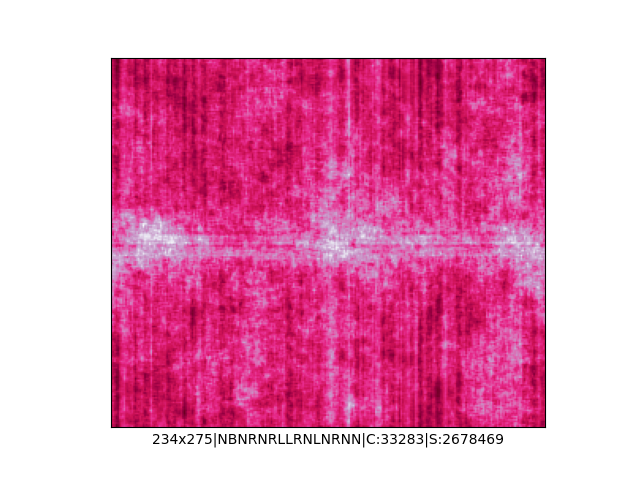


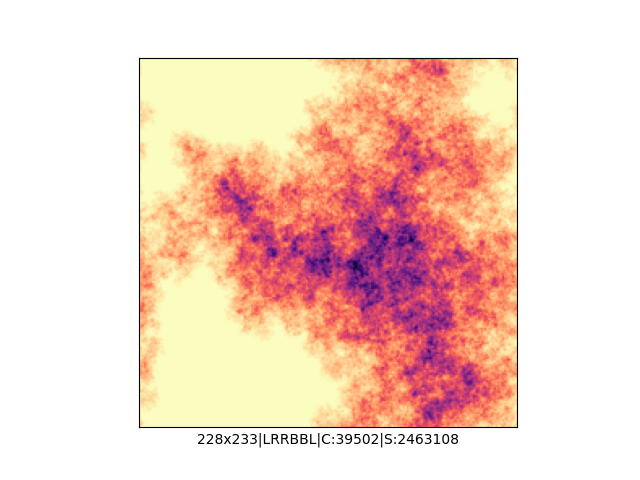










































… czyli po powierzchni torusa 🙂
No przecież mówię wyraźnie 🙂
W Minecrafcie w updacie na Prima Aprilis 2020 była możliwość obserwowania bloku poruszającego się tak, jak Mrówka Langdona (włącznie z zaczernianiem i wybielaniem bloków) Oczywiście, pojawiała się charakterystyczna autostrada. Można też było zaburzać ruch ustawiając blok w odpowiednim kolorze na trasie „mrówki” 🙂
Trochę odległe skojarzenie:
https://duckduckgo.com/?t=ffab&q=fraktal&iax=images&ia=images
Mimo, że niektóre obrazki są bardzo podobne, to chyba nie da się zmusić mrówki do rysowania fraktali.
Nie z tak losowym wybieraniem kierunku (nie ma powiązania z poprzednią pozycją).
Tu masz przykład (po ang.) na pewien fraktal: [Numberphile]
Co prawda jest losowanie, ale fraktal buduje się wedle reguły: zaznaczamy punkt w połowie odległości pomiędzy poprzednim punktem a losowym rogiem trójkąta
Kolega zaszalał z przykładami 😀
To tylko wierzchołek góry lodowej. Mam lokalnie coś ze 3K obrazków. Udało mi się zrobić to samo na planszy heksagonalnej, a potem jeszcze z mrówką skaczącą ruchem konika szachowego i króla.
Palec na telefonie by mi się zwichnął gdy jechałem do komentarza 😉