Bored with a game, I wrote a solver

https://xpil.eu/1lc 📋

Today I am going to tell you about a game I got into a few weeks ago. It's kind of addictive: very simple, click-click, tap-tap, no need to think too much. All you need is the ability to add to 10.

I am talking about the "Number Match" game. You start with a 9 columns x 3 rows board filled with random numbers from 1 to 9. The numbers have to be eliminated in pairs. A pair is either two identical numbers, or two numbers adding up to 10, so for example you can remove two 3s, or a 2 with an 8, and so on. However, the numbers in the pair to be removed must "see" each other, i.e. either be adjacent or be in a straight line (including 45 degrees) to each other - in the latter case only if there are no other numbers between them - or finally be in one horizontal line ignoring the "breaks" of the lines.

For clarity, examples below:

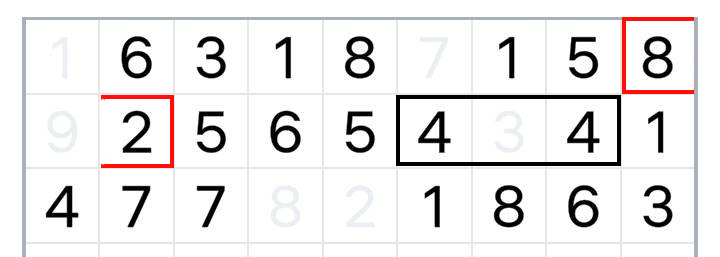
Additionally, if we clear an entire horizontal row of numbers, it disappears from the board (the rows below shift up). If we run out of moves (no more pairs), we can click a special button that will "refill" the board with more numbers - more specifically, it will take all the numbers that are currently on the board and add them to the end, starting from the first empty cell, in the same order, by rows. Example:

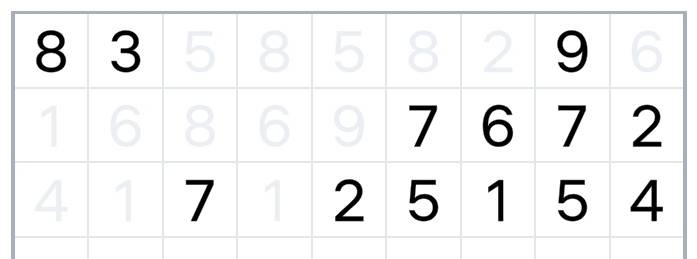
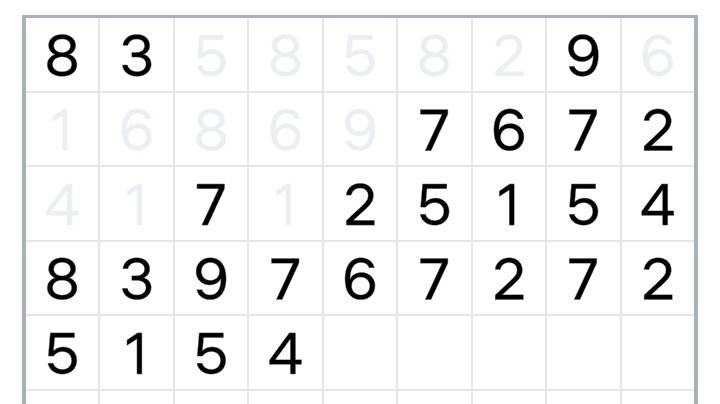
"Refilling" of new numbers can only be used four times - if we use all four and do not clear the board, we lose the game. By the way you can "refill" numbers at any time, not just when you run out of pairs. This is especially useful around the end of a board, when there are very few numbers left and a single "refill" doesn't let you solve the board, but a double (or triple) one does.

The aim of the game is to empty as many boards as possible. For each pair removed we get points, the amount of which depends on whether the numbers in the pair are in contact with each other or not, and on the consecutive number of the board (in subsequent boards pairs are scored higher and higher), although the latter is capped around board number 15 or 16 (I think).

There is also a trick: after removing a pair, if you empty the whole row, before the row disappears the game plays a half-second animation - during this animation you can still choose pairs (which resets the animation timer) - this is especially useful in difficult situations, where after removing a pair you reveal another pair on the diagonal - removing the empty row makes the pair on the diagonal disappear, but if you click on it before the row disappears, the pair will disappear too. You usually have to plan this move in advance of removing the first pair, because half a second is not much of a time.

I played this game for a couple of weeks when I realized I was wasting my time - come on, a three years old can add to ten, and stabbing at numbers with your finger is not really creative in the long run.

Having achieved the record of about 45000 points (some 20 boards) I decided that I will write myself a solver.

The idea arose partly out of boredom, and partly because at some point I realized that each board is deterministic, i.e. it is possible to search the whole tree of possible moves and find all winning variants.

So I wrote one. The solver works on the basis of the Monte Carlo method: it tries to solve the board by making random moves until it succeeds. It turns out that the average number of attempts is about 3-4 per board, so usually the solution is found almost immediately.

This solver has three small disadvantages though: firstly it doesn't take into account the half-second animation when deleting an empty line (so it can't really check all the combinations) - this is not really a problem, because it always finds the solution in 3-4 attempts anyway. The second disadvantage is that once in a while it incorrectly "refills" numbers (I don't know where the bug is exactly, and I don't care anymore - it happens very occasionally, once in a dozen of boards), thirdly it doesn't try to "refill" numbers before all moves are used up (which, again, eliminates some combinations from the problem search space)

Despite these drawbacks during testing I managed to double my own top score in the first attempt: from 45000 points (about 20 boards) I jumped to over 85000 (about 30 boards).

The solver code is rather messy - unfortunately, since it works (ish), I'm not going to improve it anymore 🙂

Here it is:

import numpy as np
from random import sample
from numpy.random.mtrand import randint
from pprint import pprint
from math import ceil
from os import system, name
from msvcrt import getch
from termcolor import colored, cprint


def unFlatten(b):
    cols = 9
    rows = ceil(len(b)/cols)
    if(len(b) % 9 > 0):
        bz = np.append(b, np.zeros(9-(len(b) % 9), dtype=int))
    else:
        bz = b
    b2d = np.reshape(bz, (rows, cols))
    return b2d


def printBoard(b, p=None):
    if(b is None):
        return
    b2d = unFlatten(b)
    if(not p is None):
        x1, y1, x2, y2 = p["x1"], p["y1"], p["x2"], p["y2"]
    else:
        x1, y1, x2, y2 = -1, -1, -1, -1
    rows = b2d.shape[0]
    cols = b2d.shape[1]
    for r in range(rows):
        for c in range(cols):
            v = b2d[r, c]
            if(v == 0):
                cprint(v, 'white', end=" ")
            elif((r == x1 and c == y1) or (r == x2 and c == y2)):
                cprint(v, color='grey', on_color='on_white', end=" ")
            else:
                print(v, end=" ")
        print()


def clrScr():
    if(name == 'nt'):
        _ = system('cls')
    else:
        _ = system('clear')


def getPairs(b):
    pairs = []
    cx, cy = 0, 0
    cursor = [cx, cy]

    b2d = unFlatten(b)

    while True:
        valueatcursor = b2d[cx, cy]
        for dirxy in [[-1, -1], [-1, 0], [-1, 1], [0, -1], [0, 1], [1, -1], [1, 0], [1, 1]]:
            distance = 1
            abort = False
            dx, dy = dirxy[0]*distance, dirxy[1]*distance
            while True:
                if(cx+dx < 0 or cx+dx >= b2d.shape[0] or cy+dy < 0 or cy+dy >= b2d.shape[1]):
                    abort = True
                    break
                else:
                    if(b2d[cx+dx, cy+dy] > 0):
                        break
                    else:
                        distance += 1
                        dx, dy = dirxy[0]*distance, dirxy[1]*distance
            if not abort:
                valueatshift = b2d[cx+dx, cy+dy]
                if(valueatcursor == valueatshift or valueatcursor+valueatshift == 10):
                    pairs.append(
                        {"x1": cx, "y1": cy, "x2": cx+dx, "y2": cy+dy})

        cx2 = cx
        cy2 = cy + 1
        if cy2 == b2d.shape[1]:
            cx2 += 1
            cy2 = 0
        if cx2 < b2d.shape[0]:
            abort2 = False

            while(b2d[cx2, cy2] == 0):
                cy2 += 1
                if(cy2 == b2d.shape[1]):
                    cy2 = 0
                    cx2 += 1
                    if(cx2 == b2d.shape[0]):
                        abort2 = True
                        break

            if not abort2:
                if valueatcursor+b2d[cx2, cy2] == 10 or valueatcursor == b2d[cx2, cy2]:
                    pairs.append(
                        {"x1": cx, "y1": cy, "x2": cx2, "y2": cy2})

        cx += 1
        if(cx == b2d.shape[0]):
            cx = 0
            cy += 1
            if(cy == b2d.shape[1]):
                break
    pairs = [dict(t) for t in {tuple(d.items()) for d in pairs}]
    return pairs


def makeMove(b, p):

    # retrieve pair coordinates
    x1, x2, y1, y2 = p["x1"], p["x2"], p["y1"], p["y2"]

    b2d = unFlatten(b)

    # remove p from board
    b2d[x1, y1] = 0
    b2d[x2, y2] = 0

    # remove rows where all elements == 0
    b2d = b2d[~np.all(b2d == 0, axis=1)]

    # revert to linear
    bflat = b2d.flatten()
    if(len(b) % 9 > 0):
        delCounter = 9-(len(b) % 9)
        bflat = bflat.tolist()
        del bflat[-delCounter:]
        bflat = np.array(bflat)
    return bflat


def spill(b):
    bnz = [n for n in b if n != 0]
    newBoard = [*b, *bnz]
    return np.array(newBoard)


def replay(s):
    for si in s:
        clrScr()
        b1, b2 = si["b1"], si["b2"]

        if(si["action"] == "init"):
            printBoard(b2)
            print("start")
        elif(si["action"] == "pair"):
            pair = si["pair"]
            printBoard(b1, pair)
            x1 = pair["x1"]
            y1 = pair["y1"]
            x2 = pair["x2"]
            y2 = pair["y2"]
            print(f"remove at ({x1},{y1}), ({x2},{y2})")
            # printBoard(b2)
        elif(si["action"] == "spill"):
            printBoard(b1)
            print("spill")
            printBoard(b2)
        elif(si["action"] == "solved"):
            print("solved")
            print(b1)
        getch()
    pprint(s)


startBoard = []

while len(startBoard) < 27:
    print("Type numbers:")
    startBoard.append(int(getch()))
    clrScr()
    printBoard(startBoard)

# startBoard = randint(1, 10, (216 ), dtype=int)
# startBoard = [0,0,0,0,0,2,0,4,3,0,0,0,0,0,0,0,8,9,0,0,8,0,0,0,4,7,0,0,0,0,0,0,0,5,1,5,0,0,0,0,0,0,7,8,3,2,4,3,8,9,8,4,7,5,1,5,7,8,3]


for trial in range(10000):
    board = startBoard.copy()
    spillsRemaining = 4
    step = 0
    solution = [{"step": step, "action": "init",
                 "b1": None, "b2": board.copy()}]
    while True:
        while True:
            step += 1
            pairs = getPairs(board)
            if(len(pairs) == 0):
                break
            pair = sample(pairs, 1)[0]
            b1 = board.copy()
            board = makeMove(board, pair)
            solution.append({"step": step, "action": "pair",
                            "pair": pair, "b1": b1, "b2": board.copy()})
            if board.shape[0] == 0:
                solution.append(
                    {"step": step, "action": "solved", "b1": b1, "b2": None, "trial": trial})
                replay(solution)
                exit(0)
        if(spillsRemaining > 0):
            b1 = board.copy()
            board = spill(board)
            solution.append(
                {"step": step, "action": "spill", "b1": b1, "b2": board.copy()})
            spillsRemaining -= 1
        else:
            break

A quick rundown of the subprocedures:

unFlatten transforms a one-dimensional board (represented by one long row) into a board with nine columns (and a corresponding number of rows depending on how many numbers are currently on the board).

printBoard displays the board in the terminal, nicely, with spaces, and with an optional highlighted pair to be removed.

clrScr clears the screen.

getPairs returns a list of all possible moves for the given board

makeMove removes the given pair from the board, removes any empty lines resulting from the move, and returns a new board (the one after the move)

spill "refills" new numbers to the end of the board

replay shows the whole game step by step, waiting for you to press a key after each move - so we can easily transfer moves from the computer screen to the game on the smartphone

Two commented lines starting with # startBoard = … are useful for testing. One generates a random 3×9 board, the other allows you to enter a specific board by hand (the latter is useful when the "refill" fails and spills the numbers differently than the game on the phone)

To work properly, the code requires four non-standard libraries: numpy, pprint, msvcrt and termcolor . (pip install…)

So, dear Reader, if your Python Force is strong, I invite you to improve the above code. Or at least to criticize this mess 🙂

https://xpil.eu/1lc 📋