Siedem mrówek z bonusem

https://xpil.eu/mxe 📋

Jakiś czas temu pisałem tu o Mrówce Langtona. Od tamtej pory temat mi trochę przysechł, ale niedawno - w ramach porządkowania plików w chmurze - odkryłem tamten folder i trochę go odkurzyłem. Dziś - z braku lepszych tematów - przegląd kilku "mrówkowych" skryptów.

1Zaczniemy od najprostszego przykładu, czyli klasycznej implementacji Mrówki Langtona (z jedną różnicą: oryginalna mrówka wędrowała po nieskończonej płaszczyźnie a moja - po powierzchni torusa).

import matplotlib.pyplot as plt
import numpy as np

dirs = {"N": [0, 1], "S": [0, -1], "W": [-1, 0], "E": [1, 0]}
L = {"N": "W", "W": "S", "S": "E", "E": "N"}
R = {"N": "E", "E": "S", "S": "W", "W": "N"}

xsize, ysize = 600,600
steps = 1000000
x, y = xsize//2, ysize//2
board = np.zeros(shape=(xsize, ysize), dtype=int)

turns = [L,R]
dir = "N"
for X in range(steps):
    dir = turns[(board[x, y])][dir]
    board[x, y] = 1-board[x, y]
    dx, dy = dirs[dir]
    x, y = (x + dx) % xsize, (y + dy) % ysize
plt.imshow(board)
plt.xticks([])
plt.yticks([])
plt.box(False)
plt.margins(0.01, 0.01)
plt.show()

Zmienna dirs przechowuje kierunki wędrówki (N - north - północ - przesunięcie o 0 w poziomie i 1 w pionie i tak dalej). Potem mamy dwie zmienne L i R - pierwsza definiuje zmiany kierunków przy zakręcie w lewo, druga - w prawo. Dla przykładu "S":"E" w zmiennej L oznacza że jeżeli szliśmy na południe (S), i chcemy skręcić w lewo (L), to po zakręcie będziemy szli na wschód ("E"). I tak dalej.

Kolejne trzy zmienne (xsize, ysize i steps) mówią nam o wielkości torusa (600x600 punktów) oraz ilości kroków mrówki (1 milion). Potem mamy x i y czyli aktualną pozycję mrówki (startujemy ze środka planszy), wreszcie samą planszę board, którą na dzień dobry wypełniamy całkowitymi zerami (linia 11).

Zanim zaczniemy wędrówkę, zbudujemy sobie jeszcze dwuelementową listę możliwych zakrętów (L i R, zmienna turns) oraz ustalimy w którą stronę mrówka jest ustawiona na początku wędrówki (dir = "N" w linii 13).

W linii 15 zaczynamy główną pętlę czyli mrówka idzie.

Linia nr 16 wymaga nieco obszerniejszego objaśnienia: otóż plansza jest binarna, a więc albo zero, albo jedynka (zero - pole puste, białe, jedynka - pole zapełnione, czarne). Zmienna dir przyjmuje kierunek kolejnego ruchu mrówki, który jest ustalany na podstawie wartości pola planszy z mrówką (board[x, y] oraz aktualnego kierunku mrówki dir). Na pierwszy rzut oka nie wygląda to może całkiem jasno, przyjrzyjmy się więc linii 16 nieco bliżej.

Zmienna turns jest ustawiona na [L, R], co w rzeczywistości oznacza, że turns == [{'N': 'W', 'W': 'S', 'S': 'E', 'E': 'N'}, {'N': 'E', 'E': 'S', 'S': 'W', 'W': 'N'}] - jest więc listą zawierającą dwa słowniki: na pozycji 0 słownik zakrętów w lewo, a na pozycji 1 - w prawo. Tym samym pierwszy indeks w linii 16 (board[x, y]) "wyłuskuje" nam ze zmiennej turns jeden z tych dwóch słowników (czyli L lub R w zależności od tego czy board[x, y] jest 0 czy 1), a drugi indeks wyciąga z tego słownika literkę oznaczającą kierunek marszu po zakręcie. W efekcie zmienna dir będzie teraz zawierać kierunek mrówki po wykonaniu zakrętu.

Ktoś mógłby mi zarzucić, że takie podejście jest zbyt skomplikowane i że prościej byłoby to zrobić na if-ach. Może i tak, ale zobaczymy w późniejszych przykładach, że dzięki takiej a nie innej organizacji danych prościej będzie nam dodać do spaceru mrówki kolejne opcje.

W linii 17 zmieniamy kolor pola pod mrówką (czyli zamieniamy na przeciwny - jeżeli była jedynka, robimy z niej zero i vice-versa).

W linii 18 ustalamy wektor przesunięcia mrówki - zmienna dirs zawiera słownik list dwuelementowych indeksowanych literkami N,S,E,W, wreszcie w linii 19 przesuwamy mrówkę na kolejne pole (czyli x+dx, y+dy), pamiętając jednak o tym, że to nie jest prostokąt tylko torus (a więc % xsize i % ysize).

Zrozumienie tego triku z dzieleniem modulo (czyli %) zajęło mi kiedyś chwilę; działa to tak: plansza (zmienna board) jest kwadratem ponumerowanym od 0 do 599 wzdłuż i w poprzek. Jeżeli mrówka jest na polu w kolumnie, dajmy na to, 599 i chcemy ją przesunąć w prawo, musielibyśmy wylądować w kolumnie numer 600, której nie ma (dostalibyśmy błąd). Dzięki podzieleniu tego 600 modulo przez 600 dostaniemy w wyniku 0 czyli pierwszą kolumnę. Jeszcze raz: przesuwamy się w prawo z ostatniej kolumny, dzięki dzieleniu modulo lądujemy w efekcie w kolumnie pierwszej (o indeksie 0) czyli "sklejamy" nasz kwadrat wzdłuż krawędzi pionowych. Identyczny proces zachodzi na krawędziach poziomych - stąd torus. Swoją drogą tak samo działa to w drugą stronę - przesunięcie w lewo z kolumny numer 0 oznacza kolumnę numer -1, której nie ma - ale -1 modulo 600 daje w wyniku 599 czyli numer ostatniej, prawej kolumny. Wszystko się zgadza.

Wykonawszy linie 15-19 milion razy pętla się zakończy i przejdziemy do części prezentacyjnej, czyli wyświetlenia trasy mrówki na obrazku.

W linii 20 wywołujemy funkcję imshow - jest to standardowa funkcja biblioteki matplotlib.pypy, która konwertuje dwuwymiarową tablicę liczb na postać graficzną (rastrową, czyli bitmapę). W liniach 21 i 22 usuwamy znaczniki z osi współrzędnych (nie potrzebujemy ich), w linii 23 usuwamy ramkę wokół obrazka, a w linii 24 - zerujemy marginesy (tak naprawdę ustawiamy je na jedną setną cala czyli prawie tyle co nic). Wreszcie w linii 25 wyświetlamy obrazek na ekranie. Efekt jest taki:

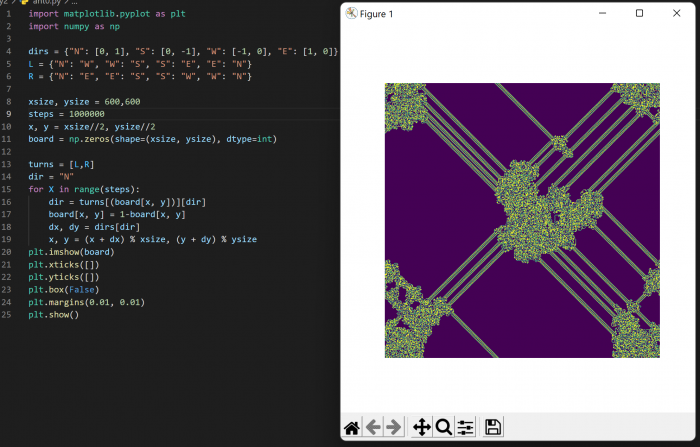
2Kolejny przykład jest nieco bardziej rozbudowany. Do oryginalnych dwóch zakrętów (w lewo i w prawo) dodajemy dwie dodatkowe opcje: "brak zakrętu" (N) oraz "zawróć" (B). Ponadto - aby program zaczął nam generować bardziej zróżnicowane obrazki - za każdym razem losujemy liczbę kolorów w palecie, a także zakres wartości pojedynczego pola, a więc z torusa binarnego przechodzimy w torus całkowitoliczbowy. Kod wygląda tak:

import matplotlib.pyplot as plt
import numpy as np
from random import choice, randrange as rr

dirs = {"N": [0, 1], "S": [0, -1], "W": [-1, 0], "E": [1, 0]}
L = {"N": "W", "W": "S", "S": "E", "E": "N"}
R = {"N": "E", "E": "S", "S": "W", "W": "N"}
N = {"N": "N", "W": "W", "S": "S", "E": "E"}
B = {"N": "S", "W": "E", "S": "N", "E": "W"}
colormaps = plt.colormaps()

for mainloop in range(10):

    xsize, ysize = 1000 + rr(200), 1000+rr(200)
    x, y = xsize//2, ysize//2
    dir = "N"
    steps, colours = 2000000 + rr(8000000), 20+rr(65515)
    board = np.zeros(shape=(xsize, ysize), dtype=int)

    turns = []
    tt = ""
    trnum = 4+rr(100)
    for i in range(trnum):
        t = choice(("L", "R", "N", "B"))
        tt += t
        turns.append({"L": L, "R": R, "N": N, "B": B}[t])

    for X in range(steps):
        dir = turns[(board[x, y]) % len(turns)][dir]
        board[x, y] = (board[x, y] + 1) % colours
        dx, dy = dirs[dir]
        x, y = (x + dx) % xsize, (y + dy) % ysize
    plt.imshow(board, cmap=choice(colormaps))
    plt.xticks([])
    plt.yticks([])
    plt.box(False)
    plt.margins(0.01, 0.01)
    plt.xlabel(f"{xsize}x{ysize}|{tt}|C:{colours}|S:{steps}")
    filename = f"py2/ants/langton-{xsize}-{ysize}-{tt}-{colours}-{steps}.png"
    plt.savefig(filename)
    plt.clf()

Początek się za bardzo nie zmienił - doszły jednak dwie dodatkowe akcje, teraz oprócz L i R mamy jeszcze N i B (N - nie zmieniaj kierunku, B - zawróć). Ponadto w linii 10 wyciągamy sobie listę wszystkich palet kolorów dostępnych w bibliotece PyPlot - będziemy z niej później losować paletę dla każdego obrazka, w celu urozmaicenia grafiki.

W linii 12 zaczynamy główną pętlę - każda jej iteracja "wypluje" w wyniku jeden plik png z obrazkiem spaceru mrówki. W przykładzie pętla wykona się 10 razy - jeżeli chcesz mieć duuuużo obrazków, ustaw ją sobie na tysiąc albo milion 🙂

W linii 14 losujemy wielkość obrazka (prostokąt o długościach boków między 1000 a 1199), a w 15 i 16 - podobnie jak w poprzednim przykładzie - ustawiamy mrówkę na środku planszy, skierowaną w górę.

W linii 17 losujemy liczbę kroków (między 2 a 10 milionów, chociaż lepiej byłoby ją uzależnić od wielkości obrazka - czym większy obrazek, tym więcej kroków - zobaczymy w późniejszych przykładach, że taka logika działa całkiem fajnie) a także liczbę kolorów w palecie (między 20 a 65534). Potem - identycznie jak poprzednio - następuje inicjalizacja torusa samymi zerami.

W liniach 20 - 26 budujemy zmienną turns (analogicznie do poprzedniego przykładu) - zawiera ona listę akcji (czyli zakrętów lub zawracań lub niezakręcania) dla poszczególnych kolorów pól. Długość tej listy jest również losowana (między 4 a 103 elementy) - i tutaj uwaga: lista akcji będzie użyta do późniejszego zbudowania nazwy pliku png, więc należy pamiętać, aby nie była ona zbyt długa.

Linie 28 - 32 to samo gęste, czyli mrówka idzie.

W linii 29 mamy działanie podobne do linii 16 z poprzedniego przykładu - jednak tu musimy dodatkowo "zawinąć" logikę za pomocą % len(turns) ponieważ liczba kolorów może być (i na ogół jest) większa od liczby możliwych akcji.

W linii 33 tworzymy obrazek - prawie identycznie jak w linii 20 z przykładu #1, tylko z dodatkowym losowaniem palety kolorów. Dalej wszystko tak samo aż do linii 38, gdzie dodatkowo wstawiamy opis pod obrazkiem - dzięki temu wiemy z jakimi parametrami był on wygenerowany (niestety dla bardzo długich list akcji opis nie mieści się w całości - ale nie szkodzi). W liniach 39 i 40 generujemy nazwę pliku wyjściowego i zapisujemy go. Proszę jednak zwrócić uwagę na początek nazwy pliku - w moim przypadku ląduje on w folderze py2/ants/ (względem lokalizacji głównego skryptu) - utwórz sobie taki folder ewentualnie zmień sobie ten początek na coś innego. Wreszcie w linii 41 czyścimy wykres do zera w celu przygotowania kolejnego obrazka.

Efekt? Dziesięć obrazków w folderze py2/ants, z najrozmaitszymi spacerami mrówek. Oczywiście trzeba odrobinę poczekać - u mnie każdy obrazek generuje się w czasie około 20 sekund, całość zajmuje więc około 3-4 minut.

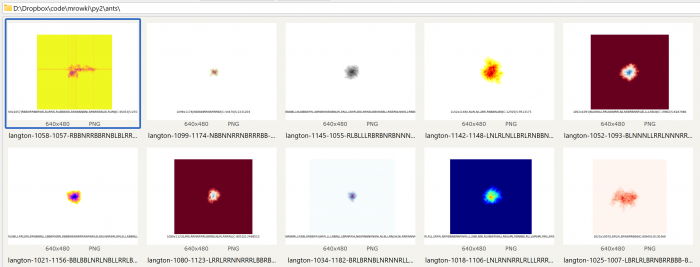
3Trzeci przykład ściągnąłem z tej strony - wrzucam żywcem jak leci, bez komentarzy (ewentualną analizę pozostawiam Czytelnikowi). Autor stosuje pi x oko podobną logikę do tego, co pokazałem powyżej - tylko tutaj jest plansza heksagonalna zamiast prostokątnej, a struktura kodu jest nieco bardziej uporządkowana.

# Langton's Ant on a hexagonal grid
# Based on: https://scipython.com/blog/langtons-ant-on-a-hexagonal-plane/

import numpy as np
import matplotlib.pyplot as plt
from random import choice


def hex_ant(n1, n2, nmoves, rules_string, cmap='hot'):

    def plot_hex(ax, i1, i2, c='#888888'):
        # Hexagon side-length.
        a = 1 / np.sqrt(3)
        # Hexagon centre (cx, cy), and vertex coordinates.
        cx, cy = i1 + 1/4 * (-1)**(i2 % 2), 3*a/2*i2
        x1, y1 = cx, cy + a
        x2, y2 = cx + 1/2, cy + a/2
        x3, y3 = cx + 1/2, cy - a/2
        x4, y4 = cx, cy - a
        x5, y5 = cx - 1/2, cy - a/2
        x6, y6 = cx - 1/2, cy + a/2
        hexagon = plt.Polygon(((x1, y1), (x2, y2), (x3, y3), (x4, y4),
                               (x5, y5), (x6, y6)), fc=c)
        ax.add_patch(hexagon)

    arr = np.zeros((n2, n1), dtype=np.uint8)

    # Moves for even and odd rows, clockwise, starting with <- ("west").
    moves = np.array([
        [(-1, 0), (0, 1), (1, 1), (1, 0), (1, -1), (0, -1)],
        [(-1, 0), (-1, 1), (0, 1), (1, 0), (0, -1), (-1, -1)]
    ])

    def parse_rules_string(s):
        move_dict = {'N': 0, 'L2': -2, 'L1': -1, 'R1': 1, 'R2': 2, 'U': 3}
        rules = []
        i = 0
        while i < len(s):
            t = s[i]
            if t in 'LR':
                i += 1
                t += s[i]
            try:
                rules.append(move_dict[t])
            except KeyError:
                raise ValueError(f'Unknown move {t} in rules {s}')
            i += 1
        return rules

    # Figure resolution and dimensions.
    DPI = 30
    width, height = 500, 500
    fig = plt.figure(figsize=(width/DPI, height/DPI), dpi=DPI, facecolor='k')
    ax = fig.add_subplot()
    # Ensure squares are square, remove padding from around Axes.
    plt.axis('equal')
    plt.subplots_adjust(top=1, bottom=0, right=1, left=0, hspace=0, wspace=0)

    rules = parse_rules_string(rules_string)
    nrules = len(rules)
    cm = plt.get_cmap(cmap)
    c = [cm(i/(nrules-1)) for i in range(nrules)]
    ax.set_facecolor(c[0])

    i1, i2 = n1 // 2, n2 // 2
    # j indexes the moves array for a given row parity: as the ant turns
    # we update j, which determines d1, d2, the change in coordinates (i1, i2)
    # of the ant.
    j = 0
    for i in range(nmoves):
        j = (j + rules[arr[i2, i1]]) % 6
        d1, d2 = moves[i2 % 2, j]
        arr[i2, i1] = (arr[i2, i1] + 1) % nrules
        i1, i2 = (i1 + d1) % n1, (i2 + d2) % n2

    for i1 in range(n1):
        for i2 in range(n2):
            if arr[i2, i1] > 0:
                plot_hex(ax, i1, i2, c[arr[i2, i1]])

    ax.set_xlim(0, n1)
    ax.set_ylim(0, n2)

    filename = f'py2/ants/hexa-{n1}x{n2}-{rules_string}.png'
    plt.savefig(filename, dpi=DPI)

# MAIN
n1, n2 = 500, 500
nmoves = 100000
for i in range(10):
    rules_string = ''.join(
        [choice(['L1', 'L1', 'L2', 'R1', 'R2', 'R2', 'N', 'U']) for i in range(20)])
    hex_ant(n1, n2, nmoves, rules_string, cmap=choice(plt.colormaps()))

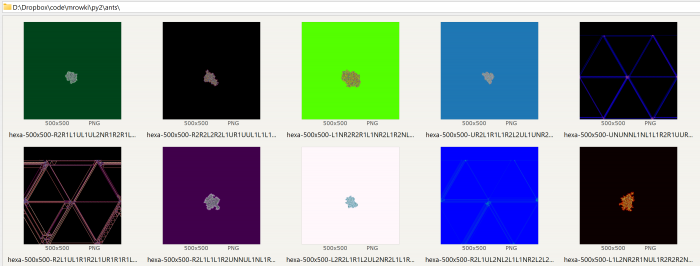
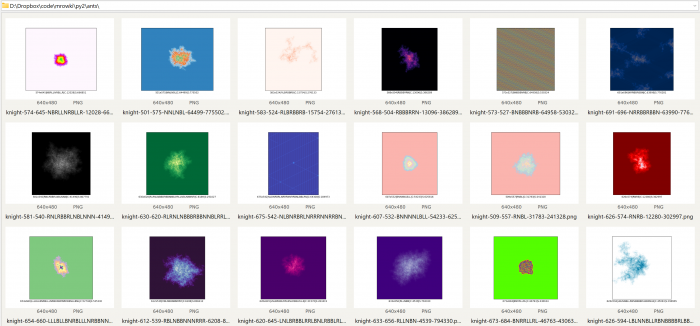
4Przykład #4 jest prawie identyczny z przykładem numer #2 z jedną zasadniczą różnicą: mrówka zamiast poruszać się po torusie ruchem króla, porusza się ruchem skoczka szachowego (czyli główne różnice między przykładem #2 a #4 to linie 8, 9 i 11).

# Langton's Ant - chess knight move pattern

import matplotlib.pyplot as plt
import numpy as np
from random import choice, randrange as rr

dirs = {"D1": [-1, 2], "D2": [1, 2], "D3": [2, 1], "D4": [2, -1], "D5": [1, -2], "D6": [-1, -2], "D7": [-2, -1], "D8": [-2, 1]}
L = {"D1": "D8","D8": "D7","D7": "D6","D6": "D5","D5": "D4","D4": "D3","D3": "D2","D2": "D1"}
R = {"D8": "D1","D7": "D8","D6": "D7","D5": "D6","D4": "D5","D3": "D4","D2": "D3","D1": "D2"}
N = {"D1": "D1","D2": "D2","D3": "D3","D4": "D4","D5": "D5","D6": "D6","D7": "D7","D8": "D8"}
B = {"D1": "D5","D2": "D6","D3": "D7","D4": "D8","D5": "D1","D6": "D2","D7": "D3","D8": "D4"}

colormaps = plt.colormaps()

for mainloop in range(1000):

    xsize, ysize = 500 + rr(200), 500+rr(200)
    steps, colours = 100000 + rr(800000), 20+rr(65515)
    x, y = xsize//2, ysize//2
    board = np.zeros(shape=(xsize, ysize), dtype=int)

    turns = []
    tt = ""
    trnum = 2+rr(30)
    for i in range(trnum):
        t = choice(("L", "R", "N", "B"))
        tt += t
        turns.append({"L": L, "R": R, "N": N, "B": B}[t])

    dir = "D2"
    for X in range(steps):
        dir = turns[(board[x, y]) % len(turns)][dir]
        board[x, y] = (board[x, y] + 1) % colours
        dx, dy = dirs[dir]
        x, y = (x + dx) % xsize, (y + dy) % ysize
    plt.imshow(board, cmap=choice(colormaps))
    plt.xticks([])
    plt.yticks([])
    xlab = "{}x{}|{}|C:{}|S:{}".format(xsize, ysize, tt, colours, steps)
    plt.xlabel(xlab)
    filename = f"py2/ants/knight-{xsize}-{ysize}-{tt}-{colours}-{steps}.png"
    plt.savefig(filename)
    plt.clf()

Proszę uważać na liczbę generowanych plików - w przykładzie powyżej skrypt utworzy 1000 obrazków 🙂

5Zamiast czterech stron świata, w tym przykładzie mrówka ma ich do wyboru aż osiem - cztery główne i cztery pośrednie ("na ukos"). Znów, jedyna różnica sprowadza się do linii 8, 9 i 11, gdzie definiujemy możliwe zakręty. Cała reszta w zasadzie bez zmian.

# Langton's Ant - 8 directions

import matplotlib.pyplot as plt
import numpy as np
from random import choice, randrange as rr

dirs = {"D1": [-1, -1], "D2": [-1, 0], "D3": [-1,1], "D4": [0, -1], "D5": [0, 1], "D6": [1, -1], "D7": [1, 0], "D8": [1, 2]}
L = {"D1": "D8","D8": "D7","D7": "D6","D6": "D5","D5": "D4","D4": "D3","D3": "D2","D2": "D1"}
R = {"D8": "D1","D7": "D8","D6": "D7","D5": "D6","D4": "D5","D3": "D4","D2": "D3","D1": "D2"}
N = {"D1": "D1","D2": "D2","D3": "D3","D4": "D4","D5": "D5","D6": "D6","D7": "D7","D8": "D8"}
B = {"D1": "D5","D2": "D6","D3": "D7","D4": "D8","D5": "D1","D6": "D2","D7": "D3","D8": "D4"}

colormaps = plt.colormaps()

for mainloop in range(10):

    xsize, ysize = 1000 + rr(200), 1000+rr(200)
    steps, colours = 500000 + rr(800000), 20+rr(20000)
    x, y = xsize//2, ysize//2
    board = np.zeros(shape=(xsize, ysize), dtype=int)

    turns = []
    tt = ""
    trnum = 2+rr(40)
    for i in range(trnum):
        t = choice(("L", "R", "N", "B"))
        tt += t
        turns.append({"L": L, "R": R, "N": N, "B": B}[t])

    dir = "D2"

    for X in range(steps):
        dir = turns[(board[x, y]) % len(turns)][dir]
        board[x, y] = (board[x, y] + 1) % colours
        dx, dy = dirs[dir]
        x, y = (x + dx) % xsize, (y + dy) % ysize
    plt.imshow(board, cmap=choice(colormaps))
    plt.xticks([])
    plt.yticks([])
    xlab = f"{xsize}x{ysize}|{tt}|C:{colours}|S:{steps}"
    plt.xlabel(xlab)
    filename = f"py2/ants/eight-{xsize}-{ysize}-{tt}-{colours}-{steps}.png"
    plt.savefig(filename)

6Od tego miejsca zaczynają się eksperymenty nieco bardziej zaawansowane. Nadal pozostajemy na dwuwymiarowej planszy prostokątnej, nadal dopuszczamy zakręty w ośmiu kierunkach (jak w przykładzie #5), jednak wprowadzamy kilka zasadniczych zmian do logiki wybierania kolejnego zakrętu. Nie da się przedstawić wszystkich możliwych wariantów (można dać się ponieść kreatywności) - chcę tylko pokazać w którą stronę można kombinować. W poniższym przykładzie po pierwsze w celu lepszej "randomizacji" obrazka staramy się, aby zarówno rozmiary jak też liczba kolorów były liczbami pierwszymi (unikamy dzięki temu "nudnych" zapętleń), po drugie zaś - dużo moim zdaniem ciekawsze - uzależniamy kolejny zakręt mrówki nie tylko od wartości koloru bieżącego pola, ale również od pewnych własności matematycznych bieżącego numeru kroku, bieżących współrzędnych oraz wielkości torusa; formułę można modyfikować w zasadzie bez ograniczeń. Tutaj do numeru kroku dodajemy miliard, potem dzielimy modulo przez iloczyn bieżących współrzędnych mrówki powiększony o sumę wymiarów planszy, następnie losujemy zakręt tylko jeżeli wynik tego działania jest liczbą pierwszą. Szczegóły w liniach 36-38:

# Langton's Ant - 8 directions - with primes (variant 1)

import matplotlib.pyplot as plt
import numpy as np
from sympy import isprime, nextprime
from random import choice, randrange as rr

dirs = {"D1": [-1, -1], "D2": [-1, 0], "D3": [-1,1], "D4": [0, -1], "D5": [0, 1], "D6": [1, -1], "D7": [1, 0], "D8": [1, 2]}
L = {"D1": "D8","D8": "D7","D7": "D6","D6": "D5","D5": "D4","D4": "D3","D3": "D2","D2": "D1"}
R = {"D8": "D1","D7": "D8","D6": "D7","D5": "D6","D4": "D5","D3": "D4","D2": "D3","D1": "D2"}
N = {"D1": "D1","D2": "D2","D3": "D3","D4": "D4","D5": "D5","D6": "D6","D7": "D7","D8": "D8"}
B = {"D1": "D5","D2": "D6","D3": "D7","D4": "D8","D5": "D1","D6": "D2","D7": "D3","D8": "D4"}

colormaps = plt.colormaps()

for mainloop in range(10):

    xsize, ysize = nextprime(1000 + rr(200)), nextprime(1000+rr(200))
    steps, colours = 1000000 + rr(1000000), nextprime(10000+rr(20000))
    x, y = xsize//2, ysize//2
    board = np.zeros(shape=(xsize, ysize), dtype=int)

    turns = []
    tt = ""
    trnum = nextprime(2+rr(10))
    for i in range(trnum):
        t = choice(("L", "R", "N", "B"))
        tt += t
        turns.append({"L": L, "R": R, "N": N, "B": B}[t])

    dir = "D2"
    dx, dy = dirs[dir]
    x, y = (x + dx) % xsize, (y + dy) % ysize

    for X in range(steps):
        if isprime((1000000000 + X) % (x * y + xsize + ysize)):
            dir = turns[(board[x, y]) % len(turns)][dir]
            dx, dy = dirs[dir]
        board[x, y] = (board[x, y] + 1) % colours
        x, y = (x + dx) % xsize, (y + dy) % ysize
    plt.imshow(board, cmap=choice(colormaps))
    plt.xticks([])
    plt.yticks([])
    plt.xlabel(f"{xsize}x{ysize}|{tt}|C:{colours}|S:{steps}")
    filename = f"py2/ants/eight-prime1-{xsize}-{ysize}-{tt}-{colours}-{steps}.png"
    plt.savefig(filename)
    plt.clf()

Przykładowe wyniki poniżej - przy okazji zauważamy, że jest to całkiem fajne narzędzie do generowania powtarzalnych tekstur (powtarzalnych tj. takich, że można nimi wypełnić większą powierzchnię w sposób "ciągły").

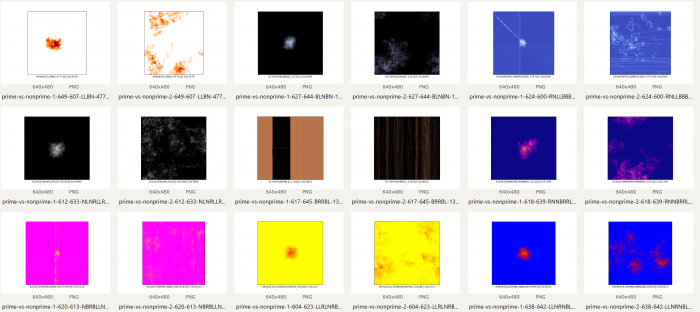
7A tutaj zobaczymy na własne oczy jak dodanie jednej "malutkiej" zmiany wpływa na generowany obrazek. Poniższy kod generuje pary obrazków - pierwszy element w parze to "zwykła" Mrówka Langtona (w ośmiu kierunkach) a drugi - prawie ta sama mrówka (tj. z identycznymi parametrami), tylko "ulepszona" poprzez dodanie sprawdzenia, czy bieżący numer kroku jest liczbą pierwszą czy nie - i jeżeli tak, odwrócenie kierunku spaceru o 180 stopni. Wersja ze sprawdzaniem pierwszości generuje o wiele ciekawsze i bardziej różnorodne obrazki.

Kod:

import matplotlib.pyplot as plt
import numpy as np
from sympy import isprime
from random import choice, randrange as rr

dirs = {"N": [0, 1], "S": [0, -1], "W": [-1, 0], "E": [1, 0]}
L = {"N": "W", "W": "S", "S": "E", "E": "N"}
R = {"N": "E", "E": "S", "S": "W", "W": "N"}
N = {"N": "N", "W": "W", "S": "S", "E": "E"}
B = {"N": "S", "W": "E", "S": "N", "E": "W"}
colormaps = plt.colormaps()

for mainloop in range(10):

    xsize, ysize = 600 + rr(50), 600+rr(50)
    steps, colours = 1000000 + rr(50000), 20+rr(65515)
    x1, y1, x2, y2 = xsize//2, ysize//2, xsize//2, ysize//2
    board1, board2 = np.zeros(shape=(xsize, ysize), dtype=int), np.zeros(shape=(xsize, ysize), dtype=int)

    turns = []
    tt = ""
    trnum = 4+rr(10)
    for i in range(trnum):
        t = choice(("L", "R", "N", "B"))
        tt += t
        turns.append({"L": L, "R": R, "N": N, "B": B}[t])

    dir1, dir2 = "N","N"
    for X in range(steps):
        dir1 = turns[(board1[x1, y1]) % len(turns)][dir1]
        board1[x1, y1] = (board1[x1, y1] + 1) % colours
        dir2 = turns[(board2[x2, y2]) % len(turns)][dir2]
        board2[x2, y2] = (board2[x2, y2] + 1) % colours
        dx1, dy1 = dirs[dir1]
        x1, y1 = (x1 + dx1) % xsize, (y1 + dy1) % ysize
        if isprime(X):
            dx2, dy2 = dx1*-1, dy1*-1
        else:
            dx2, dy2 = dx1, dy1
        x2, y2 = (x2 + dx2) % xsize, (y2 + dy2) % ysize
    cm = choice(colormaps)
    plt.imshow(board1, cmap=cm)
    plt.xticks([])
    plt.yticks([])
    xlab = f"{xsize}x{ysize}|{tt}|C:{colours}|S:{steps}"
    plt.xlabel(xlab)
    filename1 = f"py2/ants/prime-vs-nonprime-1-{xsize}-{ysize}-{tt}-{colours}-{steps}.png"
    plt.savefig(filename1)

    plt.imshow(board2, cmap=cm)
    plt.xticks([])
    plt.yticks([])
    plt.xlabel(xlab)
    filename2 = f"py2/ants/prime-vs-nonprime-2-{xsize}-{ysize}-{tt}-{colours}-{steps}.png"
    plt.savefig(filename2)
    plt.clf()

Przykładowe wyniki poniżej - należy je oglądać parami. Dla lepszego podkreślenia o co chodzi pozostawiłem tą samą paletę kolorów w każdej parze.

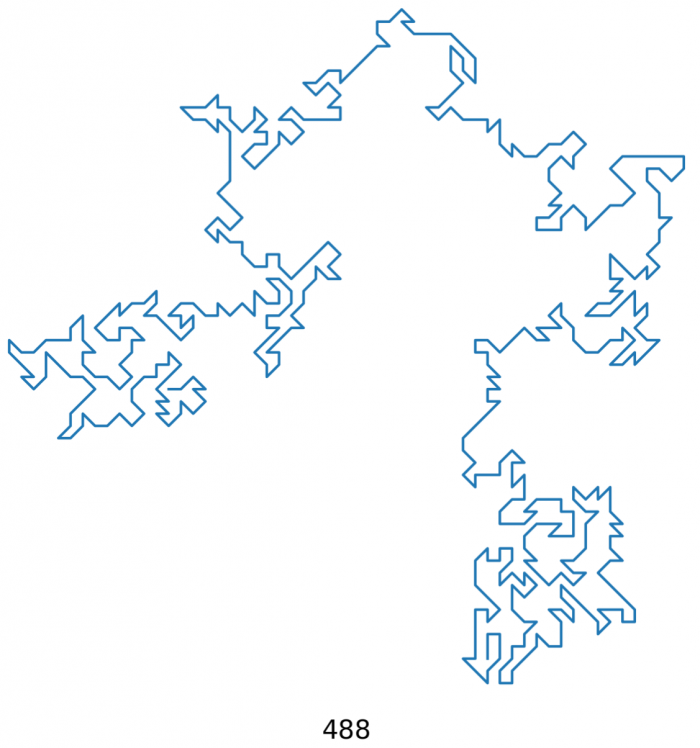
BOstatni akapit oznaczam literką "B", która wygląda trochę jak ósemka - to jest rozdział (b)onusowy dla tych, którzy dotrwali aż do tego miejsca bez powolnego oderżnięcia sobie z nudów ręki ani nogi jakimś tępym, zardzewiałym narzędziem. Otóż w wielkim skrócie zamiast ganiać biedne mrówki, tutaj wygenerujemy sobie losowy spacer po prostokątnej, nieskończonej planszy; każdy krok jest losowany spośród ośmiu kierunków świata, jednak w taki sposób, aby w żadnym miejscu nie przeciąć trasy już przebytej (w tym celu zapisujemy sobie historię ruchów, a także stosujemy trick z parzystą długością boku w celu uniknięcia błędów zaokrągleń przy wyszukiwaniu przecięć). Jeżeli się zablokujemy (tj. nie mamy więcej ruchów, bo weszliśmy w pole, z którego jedyne wyjście wymusza przecięcie już przebytej drogi), resetujemy całość do zera i zaczynamy od nowa, zapisując wynik jeżeli trasa była dłuższa od poprzedniej najdłuższej. Analizę poniższego kodu pozostawiam Czytelnikowi - dodam tylko tyle, że pętla jest nieskończona, trzeba więc program ubić klawiszem ctrl-C jak się nam już znudzi - a wynik bieżący jest zawsze zapisywany do pliku rndwalk.png, a więc poprzedni wynik jest zawsze nadpisany bieżącym. Dzięki temu aplikacja nie generuje tysięcy plików, a bieżący jest zawsze "najciekawszy" z całej serii (kolejne rozwiązania są coraz dłuższe).

Kod:

# random walk - octagonal board - do not cross path already walked
import matplotlib.pyplot as plt
from random import choice

lastN = 0

while True:
    N, retries, x, y = 0, 0, 0, 0
    kx, ky, visited = [0], [0], [[0, 0]]
    dirs = [[-2, -2], [-2, 0], [-2, 2], [0, -2],
            [0, 2], [2, -2], [2, 0], [2, 2]]

    while N < 2000:
        c = choice(range(8))
        dx, dy = [dirs[i] for i in (0, 1)]  # random direction
        newx, newy = x + dx, y + dy  # try new location

        if ([newx, newy] in visited) or ([x+dx//2, y+dy//2] in visited):
            retries += 1
            if retries > 100:
                break
        else:
            visited += [[newx, newy], [x+dx//2, y+dy//2]]
            kx.append(newx)
            ky.append(newy)
            x, y = newx, newy
            N += 1
            retries = 0

    if N > lastN:
        fig, ax = plt.subplots()
        ax.plot(kx, ky, linewidth=1, marker='')
        ax.axes.xaxis.set_ticklabels([])
        ax.axes.yaxis.set_ticklabels([])
        plt.tick_params(left=False, bottom=False)
        plt.gca().set_aspect('equal', adjustable='box')
        plt.box(False)
        plt.xlabel(f"{N}")
        plt.margins(0.01, 0.01)
        plt.savefig("rndwalk.png", dpi=300, bbox_inches='tight')
        plt.clf()
        print(N, end=" ")
        lastN = N

Przykładowe wyniki:

Mam nadzieję, że dzisiejszy wpis chociaż trochę zainteresował Cię technikami hodowli cyfrowych mrówek 🙂

https://xpil.eu/mxe 📋