Jak mówi stare przysłowie, kaca najlepiej leczyć wódką. Dzisiaj nie będę opowiadał o piciu alkoholu (patrz Ralf) tylko o gierce, w którą się wciągnąłem kilka tygodni temu. Gra z gatunku uzależniających: bardzo prosta, chętnie się klika, nie trzeba za dużo myśleć. Wystarczy umiejętność dodawania do 10.
Mowa o grze "Number Match". Zaczynamy od planszy 9 kolumn x 3 wiersze wypełnionej losowymi liczbami 1-9. Liczby trzeba likwidować parami. Para to albo dwie identyczne liczby, albo liczby dające w sumie 10. A więc można zdjąć dwie trójki albo dwójkę z ósemką i tak dalej. Z tym, że liczby w zdejmowanej parze muszą się "widzieć", a więc albo ze sobą sąsiadować, albo być względem siebie po linii prostej (włączając skosy 45 stopni) - w tym drugim przypadku tylko jeżeli nie ma między nimi żadnych innych liczb - albo wreszcie być w jednej linii poziomej ignorując "złamania" wierszy.
Dla jasności, przykłady poniżej:
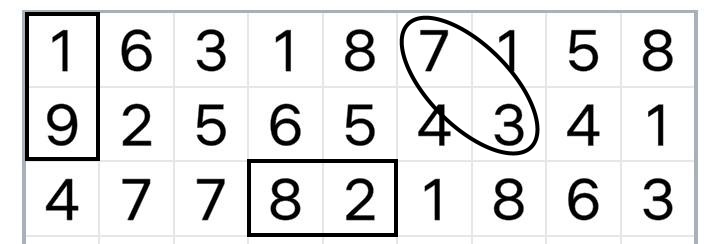
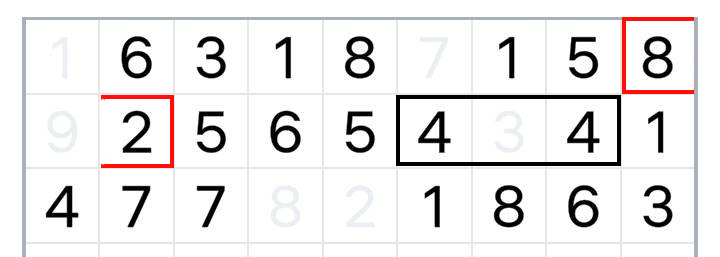
Dodatkowo jeżeli zlikwidujemy cały poziomy rząd liczb, znika on z planszy (rzędy poniżej przesuwają się w górę).
Jeżeli skończą nam się ruchy (nie ma więcej par), możemy kliknąć specjalny guzik, który "doleje" nam na planszę więcej liczb - a konkretniej weźmie wszystkie liczby, które aktualnie są na planszy i dostawi je na końcu, poczynając od pierwszego pustego pola, w tej samej kolejności, wierszami. Przykład:
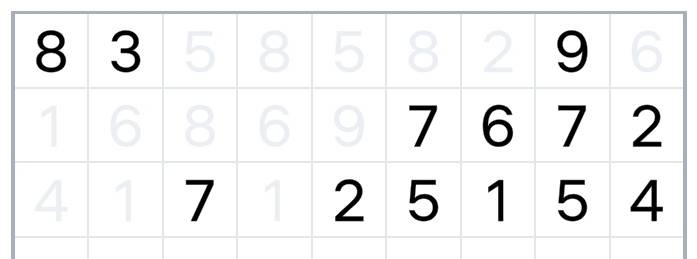
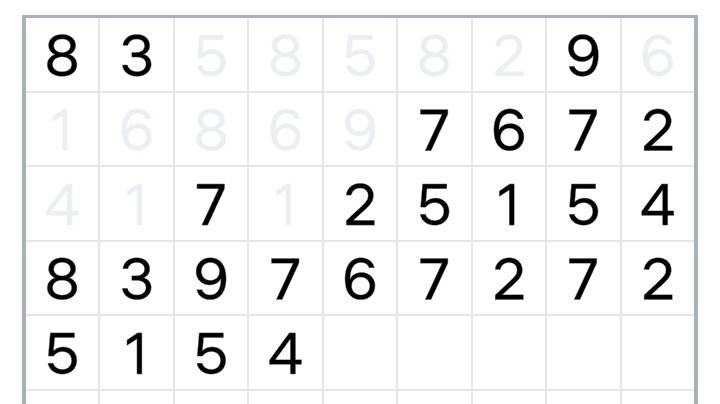
"Dolać" nowe liczby można tylko cztery razy - jeżeli wykorzystamy wszystkie cztery i nie wyzerujemy planszy, gra się kończy. Aha, "dolać" liczby można w dowolnym momencie, a nie tylko wtedy, kiedy skończą nam się pary. Przydaje się to zwłaszcza w grze końcowej, kiedy zostało bardzo mało liczb i pojedyncze "dolanie" nie rozwiąże planszy, ale już podwójne (tzn. raz za razem) - owszem.
Celem gry jest opróżnić jak najwięcej plansz. Za każdą zdjętą parę dostajemy punkty, przy czym ilość punktów jest uzależniona od tego, czy liczby w parze się ze sobą stykają czy nie, oraz od numeru planszy (w kolejnych planszach pary są punktowane coraz wyżej).
Aha, jest jeszcze jedna opcja: po zdjęciu pary, jeżeli opróżni się przy okazji cały wiersz, przed zniknięciem tego pustego wiersza gra robi mniej więcej półsekundową animację - w trakcie tej animacji można nadal wybierać pary (co resetuje timer animacji) - przydaje się to zwłaszcza przy trudnych ustawieniach, gdzie po zdjęciu pary odsłaniamy sobie inną parę po skosie - usunięcie pustego wiersza sprawi, że para po skosie zniknie, ale jeżeli zdążymy ją kliknąć zanim wiersz zniknie, to para też zniknie. Na ogół trzeba sobie taki ruch zaplanować przed zdjęciem pierwszej pary, bo pół sekundy to nie jest zbyt wiele czasu.
No więc poklikałem sobie w tę gierkę przez kilka tygodni aż w końcu stwierdziłem, że się marnuję - no bo bez przesady, dodawać do dziesięciu można nauczyć trzylatka, a takie dźganie paluchem w cyferki na dłuższą metę jest jednak mało ciekawe.
Ugrawszy więc rekord w okolicach 45000 punktów (na oko jakieś 20 plansz) stwierdziłem, że napiszę sobie solvera.
Po naszemu: rozwiązywacza, chociaż "solver" bardziej mi się podoba.
Pomysł pojawił się trochę z nudów, a trochę dlatego, że w pewnej chwili uświadomiłem sobie, że każda plansza jest przecież absolutnie deterministyczna tj. da się przeszukać całe drzewo kombinacji i znaleźć wszystkie warianty wygrywające.
No i sobie napisałem. Solver działa na zasadzie metody Monte Carlo, a więc próbuje rozwiązać planszę wykonując losowe ruchy tak długo, aż mu się uda. Okazuje się, że średnia ilość prób wynosi mniej więcej 3-4, więc rozwiązanie znajduje się praktycznie natychmiast.
Solver ów ma trzy niewielkie wady: po pierwsze nie uwzględnia tej półsekundowej animacji przy kasowaniu pustego wiersza (a więc nie jest w stanie tak naprawdę sprawdzić wszystkich kombinacji) - tu kłopot jest niewielki, bo i tak zawsze znajduje rozwiązanie w 3-4 podejściach. Druga wada jest taka, że raz na jakiś czas nieprawidłowo "rozlewa" liczby (nie wiem jeszcze dlaczego i nie chce mi się już kombinować - zdarza się to naprawdę rzadko, raz na kilkanaście plansz), po trzecie w końcu nie dopuszcza możliwości "dolewania" liczb przed wyczerpaniem wszystkich ruchów.
Pomimo tych wad podczas testów udało mi się w pierwszym podejściu pobić własny rekord (wydziergany pracowicie, przypominam, przez kilka tygodni) prawie dwukrotnie: z 45000 punktów (około 20 plansz) skoczyłem na ponad 85000 (około 30 plansz).
Kod solvera jest raczej bałaganiarski - niestety ponieważ działa (po japońsku - Jako Tako - ale działa), nie zamierzam go już poprawiać 🙂
Oto i on:
import numpy as np
from random import sample
from numpy.random.mtrand import randint
from pprint import pprint
from math import ceil
from os import system, name
from msvcrt import getch
from termcolor import colored, cprint
def unFlatten(b):
cols = 9
rows = ceil(len(b)/cols)
if(len(b) % 9 > 0):
bz = np.append(b, np.zeros(9-(len(b) % 9), dtype=int))
else:
bz = b
b2d = np.reshape(bz, (rows, cols))
return b2d
def printBoard(b, p=None):
if(b is None):
return
b2d = unFlatten(b)
if(not p is None):
x1, y1, x2, y2 = p["x1"], p["y1"], p["x2"], p["y2"]
else:
x1, y1, x2, y2 = -1, -1, -1, -1
rows = b2d.shape[0]
cols = b2d.shape[1]
for r in range(rows):
for c in range(cols):
v = b2d[r, c]
if(v == 0):
cprint(v, 'white', end=" ")
elif((r == x1 and c == y1) or (r == x2 and c == y2)):
cprint(v, color='grey', on_color='on_white', end=" ")
else:
print(v, end=" ")
print()
def clrScr():
if(name == 'nt'):
_ = system('cls')
else:
_ = system('clear')
def getPairs(b):
pairs = []
cx, cy = 0, 0
cursor = [cx, cy]
b2d = unFlatten(b)
while True:
valueatcursor = b2d[cx, cy]
for dirxy in [[-1, -1], [-1, 0], [-1, 1], [0, -1], [0, 1], [1, -1], [1, 0], [1, 1]]:
distance = 1
abort = False
dx, dy = dirxy[0]*distance, dirxy[1]*distance
while True:
if(cx+dx < 0 or cx+dx >= b2d.shape[0] or cy+dy < 0 or cy+dy >= b2d.shape[1]):
abort = True
break
else:
if(b2d[cx+dx, cy+dy] > 0):
break
else:
distance += 1
dx, dy = dirxy[0]*distance, dirxy[1]*distance
if not abort:
valueatshift = b2d[cx+dx, cy+dy]
if(valueatcursor == valueatshift or valueatcursor+valueatshift == 10):
pairs.append(
{"x1": cx, "y1": cy, "x2": cx+dx, "y2": cy+dy})
cx2 = cx
cy2 = cy + 1
if cy2 == b2d.shape[1]:
cx2 += 1
cy2 = 0
if cx2 < b2d.shape[0]:
abort2 = False
while(b2d[cx2, cy2] == 0):
cy2 += 1
if(cy2 == b2d.shape[1]):
cy2 = 0
cx2 += 1
if(cx2 == b2d.shape[0]):
abort2 = True
break
if not abort2:
if valueatcursor+b2d[cx2, cy2] == 10 or valueatcursor == b2d[cx2, cy2]:
pairs.append(
{"x1": cx, "y1": cy, "x2": cx2, "y2": cy2})
cx += 1
if(cx == b2d.shape[0]):
cx = 0
cy += 1
if(cy == b2d.shape[1]):
break
pairs = [dict(t) for t in {tuple(d.items()) for d in pairs}]
return pairs
def makeMove(b, p):
# retrieve pair coordinates
x1, x2, y1, y2 = p["x1"], p["x2"], p["y1"], p["y2"]
b2d = unFlatten(b)
# remove p from board
b2d[x1, y1] = 0
b2d[x2, y2] = 0
# remove rows where all elements == 0
b2d = b2d[~np.all(b2d == 0, axis=1)]
# revert to linear
bflat = b2d.flatten()
if(len(b) % 9 > 0):
delCounter = 9-(len(b) % 9)
bflat = bflat.tolist()
del bflat[-delCounter:]
bflat = np.array(bflat)
return bflat
def spill(b):
bnz = [n for n in b if n != 0]
newBoard = [*b, *bnz]
return np.array(newBoard)
def replay(s):
for si in s:
clrScr()
b1, b2 = si["b1"], si["b2"]
if(si["action"] == "init"):
printBoard(b2)
print("start")
elif(si["action"] == "pair"):
pair = si["pair"]
printBoard(b1, pair)
x1 = pair["x1"]
y1 = pair["y1"]
x2 = pair["x2"]
y2 = pair["y2"]
print(f"remove at ({x1},{y1}), ({x2},{y2})")
# printBoard(b2)
elif(si["action"] == "spill"):
printBoard(b1)
print("spill")
printBoard(b2)
elif(si["action"] == "solved"):
print("solved")
print(b1)
getch()
pprint(s)
startBoard = []
while len(startBoard) < 27:
print("Type numbers:")
startBoard.append(int(getch()))
clrScr()
printBoard(startBoard)
# startBoard = randint(1, 10, (216 ), dtype=int)
# startBoard = [0,0,0,0,0,2,0,4,3,0,0,0,0,0,0,0,8,9,0,0,8,0,0,0,4,7,0,0,0,0,0,0,0,5,1,5,0,0,0,0,0,0,7,8,3,2,4,3,8,9,8,4,7,5,1,5,7,8,3]
for trial in range(10000):
board = startBoard.copy()
spillsRemaining = 4
step = 0
solution = [{"step": step, "action": "init",
"b1": None, "b2": board.copy()}]
while True:
while True:
step += 1
pairs = getPairs(board)
if(len(pairs) == 0):
break
pair = sample(pairs, 1)[0]
b1 = board.copy()
board = makeMove(board, pair)
solution.append({"step": step, "action": "pair",
"pair": pair, "b1": b1, "b2": board.copy()})
if board.shape[0] == 0:
solution.append(
{"step": step, "action": "solved", "b1": b1, "b2": None, "trial": trial})
replay(solution)
exit(0)
if(spillsRemaining > 0):
b1 = board.copy()
board = spill(board)
solution.append(
{"step": step, "action": "spill", "b1": b1, "b2": board.copy()})
spillsRemaining -= 1
else:
break
Szybkie omówienie podprocedur:
unFlatten przekształca planszę jednowymiarową (jeden dłuuuugi wiersz) w planszę o dziewięciu kolumnach (i odpowiedniej ilości wierszy zależnej od tego, ile aktualnie jest liczb na planszy).
printBoard wyświetla planszę w terminalu, ładnie, ze spacjami oraz z opcjonalnie podświetloną parą do zdjęcia.
clrScr czyści ekran.
getPairs zwraca listę wszystkich możliwych ruchów dla zadanej planszy
makeMove usuwa z podanej planszy podaną parę, usuwa ewentualne puste wiersze powstałe w wyniku ruchu oraz oraz zwraca nową planszę (tę po wykonaniu ruchu)
spill "dolewa" nowe liczby na koniec planszy
replay pokazuje przebieg całej gry krok po kroku, czekając na wciśnięcie klawisza po każdym ruchu - dzięki temu możemy sobie łatwo przenieść ruchy z ekranu komputera do gry na smartfonie
Dwie zakomentowane linie zaczynające się od # startBoard = ... przydają się przy testowaniu. Jedna generuje losową planszę 3x9, druga pozwala na wpisanie konkretnej planszy z ręki (to ostatnie przydaje się kiedy spill zadziała z błędem i rozleje liczby inaczej, niż gra na telefonie)
Do poprawnej pracy kod wymaga czterech niestandardowych bibliotek numpy, pprint, msvcrt i termcolor. (pip install...)
Jeżeli, Czytelniku, czujesz się mocny w Pythonie, zapraszam do poprawienia powyższego kodu. Albo chociaż do skrytykowania tego bałaganu 🙂 Ja osobiście po napisaniu tego kodu (co zajęło mi, z przerwami, około trzech dni) mam tej gry serdecznie dosyć - pokonałem wroga wrogiem 🙂
Ciekawie…