Pchełki Python: oszukujemy w Literaki (odsłona druga)

https://xpil.eu/d4gd

W poprzednim wpisie pokazałem jak zbudować prosty anagramator do gier słownych. Rozwiązanie polegało na wygenerowaniu dla każdego słowa odpowiadającego mu "haszu" (czyli liter tego słowa posortowanych alfabetycznie), zapisanie każdego z tych "haszów" (wraz z listą jego słów "źródłowych") jako słownika (w sensie programistycznym, nie papierowym), wreszcie odpytywanie użytkownika o zawartość stojaka, posortowanie tej zawartości i przeszukanie słownika.

To jest rzecz jasna wersja uproszczona, faktycznie dopuszczamy jeszcze blanki (maksymalnie dwa), które nieco komplikują sytuację. Ale ogólna zasada się zgadza

W tamtym wpisie wspominam też, że "porządne" rozwiązanie opierałoby się pewnie na jakiejś strukturze drzewa. Nie dawało mi to spokoju i postanowiłem spróbować zaimplementować swoje pierwsze w życiu drzewo typu Trie. Jest to struktura względnie prosta do ogarnięcia nawet przez takiego głąba jak ja, a jednocześnie na tyle interesująca, że warta wpisu.

O sssso chozzzi?

Chozzzi o to, że zamiast zapisywać każdy wyraz jako osobną całość, budujemy specjalne drzewo zawierające cały słownik, wszystkie słowa na raz. Każdy element drzewa (fachowcy używają zdaje się słowa "węzeł") reprezentuje pojedynczą literę. Litera może mieć "dzieci", tj litery, które mogą po niej nastąpić. Jeżeli na przykład w słowniku będziemy mieć tylko trzy słowa: "dupa", "durny" i "dusza", to litera "d" będzie miała tylko jednego potomka ("u"), natomiast litera "u" będzie miała trzech potomków: "p", "r" i "s". Całe drzewko natomiast będzie wyglądać tak:

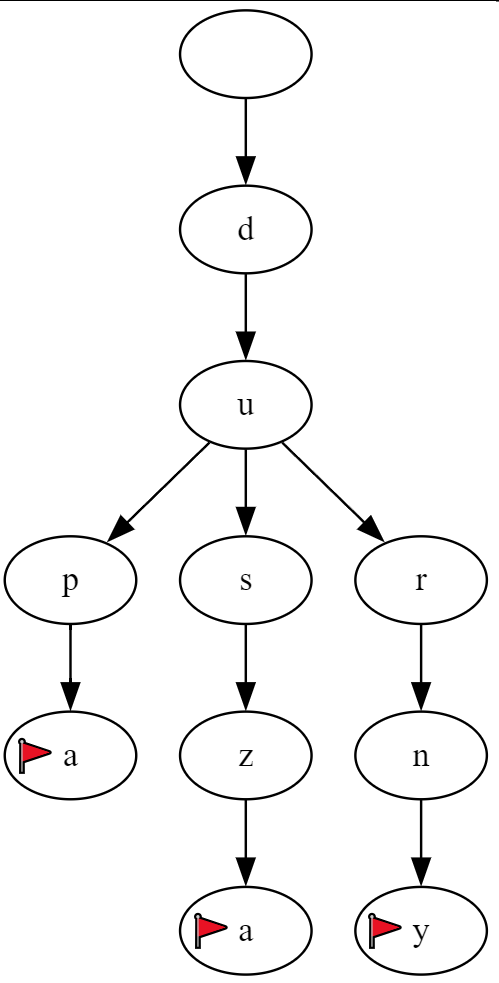
Flagi oznaczają końcówki słów. Oczywiście kompletny słownik będzie również zawierał odmiany oraz inne słowa, więc powyższy fragment drzewa wyglądałby faktycznie tak:

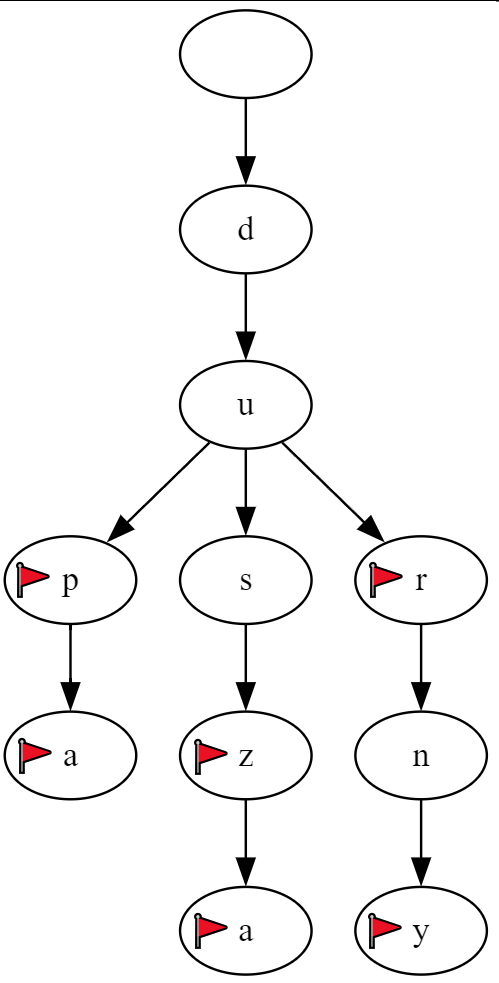
Zauważamy, że każdy element drzewa ma dokładnie jednego rodzica. Jest to obserwacja dość istotna, oznacza bowiem, że do dowolnej litery w drzewie można dotrzeć w dokładnie jeden sposób.

Słownik pobrany ze strony sjp.pl zawiera 3.18 milionów słówek składających się z około 40 milionów liter. Tyle też elementów będzie musiało zawierać nasze drzewo. Jednak ponieważ szukamy anagramów (i pod-anagramów), drzewo tak naprawdę będzie w swoich węzłach przechowywać kolejne litery "haszów", a tam, gdzie znajduje się flaga, również listę słów z tymi haszami związanych. Dzięki temu przeszukanie tej struktury powinno być niezwykle szybkie, a po dotarciu do końca haszu będziemy mieli od razu dostęp do listy możliwych słów.

Jak zwykle sprawę komplikuje nieco obecność blanków, które powiększają przestrzeń przeszukiwanych haszów 32-krotnie (przy pojedynczym blanku) lub nawet 1024-krotnie (przy podwójnym), jednak w dalszym ciągu powinno być bardzo szybko.

Czy szybciej niż przy tradycyjnym przeszukiwaniu słownika? Zobaczymy.

Czujny Czytelnik mógłby jeszcze zapytać "A dlaczego na samej górze drzewa mamy puste kółko?" i byłoby to całkiem solidne pytanie. Odpowiedź brzmi "Bo tak!", a jak się komuś taka odpowiedź nie podoba, to mam drugą, niewiele lepszą: "Bo od czegoś trzeba zacząć", a jak się komuś i ta odpowiedź nie podoba, to niech sobie przypomni stary kawał o niedźwiedziu i zającu, co bez czapki chodził.

Po tym lekko przydługim i głupawym wstępie przejdźmy do meritum, czyli napiszmy sobie w końcu jakiś kawałek kodu. Żeby było bardziej profesjonalnie, poukładamy sobie to nasze drzewko w klasy.

Zaczniemy od pojedynczego elementu drzewa:

class ElementDrzewa:
    def __init__(self):
        self.dzieci = {}
        self.końcówka = False
        self.słowa = []

Element drzewa zawiera zbiór dzieci (które również są tej samej klasy ElementDrzewa), flagę czy kończy słowo czy nie, wreszcie listę słów, które da się zbudować z liter, którymi tutaj "dotarliśmy".

-- Zaraz! Zaraz! - Wykrzyknie czujny Czytelnik - A gdzie najważniejsze, czyli literka związana z danym elementem?

I tu jest haczyk pogrzebany, jako że literki jako takiej nie ma. Nie ma i już. Albowiem literkami będziemy indeksować potomków danego elementu, więc jedyne miejsce, gdzie będą one siedzieć, to indeksy. Dzięki temu dostęp do nich będzie naprawdę szybki.

No dobra. Mamy zdefiniowany pojedynczy element drzewa, czas na drzewo:

class Drzewo:
    def __init__(self):
        self.korzeń = ElementDrzewa()

I co, i to wszystko? Na pewno?

Oczywiście, że nie. Drzewo ma pusty korzeń, który jak to często bywa w świecie komputerów jest na górze (co zresztą widać na obrazkach powyżej), ale oprócz tego potrzebujemy kilku funkcji / metod do zarządzania danymi w drzewie. A więc:

class Drzewo:
    def __init__(self):
        self.korzeń = ElementDrzewa()

    def wstaw(self, słowo: str):
        pass

    def szukaj(self, litery: str):
        pass

Potrzebujemy sposobu na wypełnienie drzewa słowami, co załatwi nam metoda wstaw(), a także sposobu na wyszukanie wszystkich anagramów, czyli metoda szukaj() - w przeciwnym razie drzewo będzie sobie po prostu rosło i szumiało na bezdurno, zjadając nam bezcenne cykle CPU zamiast pracować na swoją porcję dwutlenku węgla jak pambuk przykazał.

Czas zakasać rękawy i zabrać się do kodowania. Zaczniemy od wstaw() bo raz, jest pierwsza na liście, a dwa, łatwiejsza do napisania:

    def wstaw(self, słowo: str):
        posortowane = ''.join(sorted(słowo))
        element = self.korzeń
        for znak in posortowane:
            if znak not in element.dzieci:
                element.dzieci[znak] = ElementDrzewa()
            element = element.dzieci[znak]
        element.końcówka = True
        element.słowa.append(słowo)

Podejście jest nieco nieintuicyjne, ale działa. Zaczynamy od posortowania liter (czyli "wyliczenia hasza", proszę się nie czepiać terminologii), a potem dla każdej litery - zaczynając od samej góry - sprawdzamy, czy litera już jest wśród dzieci, czy też trzeba ją dorobić. Jeżeli trzeba dorobić, to wstawiamy do listy .dzieci kolejny ElementDrzewa (pod indeksem tej właśnie litery). A na koniec, po dodaniu ostatniej litery hasza, ustawiamy flagę, że to jest koniec słowa i dodajemy słowo do listy słów "pasujących" do tego hasza.

Następnym krokiem jest samo gęste, czyli metoda szukująca anagramów w naszym drzewie, dla zadanych liter wejściowych:

    def szukaj(self, litery):
        możliwe_kombinacje = self._generator_kombinacji(litery)
        wynik = set()

        for kombinacja in możliwe_kombinacje:
            self._szukaj_rekurencyjnie(self.korzeń, kombinacja, wynik)
            
        return sorted(list(wynik), key=len, reverse=True)

Było-ż by li to takie proste? W zasadzie, z lotu ptaka, to się pi x drzwi zgadza, ale diabeł jak zwykle siedzi w szczegółach. Widzimy tutaj bowiem wywołania dwóch kolejnych metod: _generator_kombinacji() oraz _szukaj_rekurencyjnie(). Nazwy ich zaczynają się od znaku podkreślenia w celu podkreślenia faktu, że są to metody "wewnętrzne" klasy.

Python, o ile mi wiadomo, nie umożliwia tworzenia metod prywatnych, jak na przykład C++ czy Java i trzeba się uciekać do takich protez.

Cóż to zatem za metody?

_generator_kombinacji() pozwoli nam wygenerować wszystkie kombinacje liter, z uwzględnieniem blanków oraz faktu, że szukamy nie tylko słówek N-literowych, ale także (N-1)-literowych, (N-2) i tak dalej aż do dwuliterowych.

Natomiast metoda _szukaj_rekurencyjnie() robi dokładnie to, co pisze na opakowaniu, czyli leci po drzewku poczynając od korzenia w dół (przypominam raz jeszcze, że drzewa komputerowe rosną korzeniami do góry) aż natrafi na końcówkę słowa lub zużyje wszystkie litery hasza.

Napiszmy sobie teraz te dwie metody:

        def _generator_kombinacji(self, słowo):

            def generator_podciągów(s):
                for długość in range(len(s), 1, -1):
                    for kombinacja in combinations(s, długość):
                        yield sorted(''.join(kombinacja))

        if '.' not in słowo:
            yield from generator_podciągów(słowo)
            return

        alfabet = 'aąbcćdeęfghijklłmnńoóprsśtuwyzźż'
        if słowo.count('.') == 1:
            for litera in alfabet:
                zamienione = słowo.replace('.', litera, 1)
                yield from generator_podciągów(zamienione)

        elif słowo.count('.') == 2:
            for litera1 in alfabet:
                for litera2 in alfabet:
                    zamienione = słowo.replace('.', litera1, 1).replace('.', litera2, 1)
                    yield from generator_podciągów(zamienione)

        return []

W ramach generatora kombinacji zdefiniowaliśmy sobie jeszcze wewnętrzny generator podciągów, załatwiający kwestię różnych długości pod-haszy. A potem sprawdzamy czy są blanki czy ich nie ma i w zależności od tego podmieniamy albo nie podmieniamy blanka na każdą literę alfabetu (raz albo dwa razy) i tak to leci. Ostatnia linijka funkcji to zabezpieczenie na wypadek gdyby ktoś się za bardzo rozhasał i spróbował wpisać więcej niż dwa blanki - w takim przypadku funkcja pokaże środkowy palec, czyli zwróci pustą listę.

    def _szukaj_rekurencyjnie(self, element, pozostałe_litery, wynik):
        if element.końcówka:
            wynik.update(element.słowa)

        if not pozostałe_litery:
            return

        kolejna_litera = pozostałe_litery[0]
        if kolejna_litera in element.dzieci:
            self._szukaj_rekurencyjnie(
                element.dzieci[kolejna_litera], pozostałe_litery[1:], wynik)

Podoba mi się w Pythonie to, że domyślnie parametry typu złożonego (listy, słowniki itd) są przekazywane jako referencja, więc nie dość, że jest szybko, to jeszcze dużo prościej pisze się logikę rekurencyjną. Tu na przykład budujemy sobie parametr wynik.

Jeszcze jedna funkcja, tym razem już globalna, która odczyta plik ze słówkami i zwróci nam instancję klasy Drzewo:

def zbuduj_drzewo(nazwa_pliku: str) -> Drzewo:
    drzewo = Drzewo()
    with open(nazwa_pliku, 'r', encoding='utf-8') as plik:
        for linia in plik:
            słowo = linia.strip()
            drzewo.wstaw(słowo)
    return drzewo

Teraz mamy już komplet narzędzi i możemy zabrać się za część główną. Podobnie jak ostatnio, tutaj również stosujemy trick z zapisaniem sobie całego drzewa do pliku .pkl żeby nie przeliczać go od zera za każdym razem:

if __name__ == "__main__":
    nazwa_pliku = r'slowka\trie.pkl'
    if os.path.exists(nazwa_pliku):
        with open(nazwa_pliku, 'rb') as plik:
            drzewo = pickle.load(plik)
    else:
        drzewo = zbuduj_drzewo("slowka\words.txt")
        with open(nazwa_pliku, 'wb') as plik:
            pickle.dump(drzewo, plik)

    while True:
       literki = input("Wpisz co masz na stojaku. Blank zastąp kropką. (Ctrl-C aby zakończyć): ")
       wyniki = drzewo.szukaj(literki)
       if wyniki:
           print(f"Znaleziono:", ", ".join(wyniki))
       else:
           print("Niczego nie znaleziono.")

Oczywiście nie obejdzie się też bez kilku bibliotek:

from itertools import combinations
import pickle
import os

Całość wygląda tak:

from itertools import combinations
import pickle
import os


class ElementDrzewa:
    def __init__(self):
        self.dzieci = {}
        self.końcówka = False
        self.słowa = []


class Drzewo:
    def __init__(self):
        self.korzeń = ElementDrzewa()

    def wstaw(self, słowo: str):
        posortowane = ''.join(sorted(słowo))
        element = self.korzeń
        for znak in posortowane:
            if znak not in element.dzieci:
                element.dzieci[znak] = ElementDrzewa()
            element = element.dzieci[znak]
        element.końcówka = True
        element.słowa.append(słowo)

    def szukaj(self, litery):
        możliwe_kombinacje = self._generator_kombinacji(litery)
        wynik = set()

        for kombinacja in możliwe_kombinacje:
            self._szukaj_rekurencyjnie(self.korzeń, kombinacja, wynik)
            
        return sorted(list(wynik), key=len, reverse=True)

    def _generator_kombinacji(self, słowo):
        def generator_podciągów(s):
            for długość in range(len(s), 1, -1):
                for kombinacja in combinations(s, długość):
                    yield sorted(''.join(kombinacja))

        if '.' not in słowo:
            yield from generator_podciągów(słowo)
            return

        alfabet = 'aąbcćdeęfghijklłmnńoóprsśtuwyzźż'
        if słowo.count('.') == 1:
            for litera in alfabet:
                zamienione = słowo.replace('.', litera, 1)
                yield from generator_podciągów(zamienione)

        elif słowo.count('.') == 2:
            for litera1 in alfabet:
                for litera2 in alfabet:
                    zamienione = słowo.replace('.', litera1, 1).replace('.', litera2, 1)
                    yield from generator_podciągów(zamienione)

        return []
    
    def _szukaj_rekurencyjnie(self, element, pozostałe_litery, wynik):
        if element.końcówka:
            wynik.update(element.słowa)

        if not pozostałe_litery:
            return

        kolejna_litera = pozostałe_litery[0]
        if kolejna_litera in element.dzieci:
            self._szukaj_rekurencyjnie(
                element.dzieci[kolejna_litera], pozostałe_litery[1:], wynik)


def zbuduj_drzewo(nazwa_pliku: str) -> Drzewo:
    drzewo = Drzewo()
    with open(nazwa_pliku, 'r', encoding='utf-8') as plik:
        for linia in plik:
            słowo = linia.strip()
            drzewo.wstaw(słowo)
    return drzewo


if __name__ == "__main__":
    nazwa_pliku = r'slowka\trie.pkl'
    if os.path.exists(nazwa_pliku):
        with open(nazwa_pliku, 'rb') as plik:
            drzewo = pickle.load(plik)
    else:
        drzewo = zbuduj_drzewo("slowka\words.txt")
        with open(nazwa_pliku, 'wb') as plik:
            pickle.dump(drzewo, plik)

    while True:
       literki = input("Wpisz co masz na stojaku. Blank zastąp kropką. (Ctrl-C aby zakończyć): ")
       wyniki = drzewo.szukaj(literki)
       if wyniki:
           print(f"Znaleziono:", ", ".join(wyniki))
       else:
           print("Niczego nie znaleziono.")

Zadziwiającym zbiegiem okoliczności (czy aby na pewno?) nasz kod ma dokładnie tyle samo linijek co ostatnio!

Skrypt z punktu użytkownika działa tak samo jak poprzednia wersja (oparta na prostym słowniku). A jak z prędkością działania?

Napisałem sobie pętlę generującą losowe, siedmioliterowe stojaki (plus ewentualne blanki) i zapuściłem ją parę-/naście-/dziesiąt tysięcy razy, mierząc za każdym razem czas wykonania, oto wyniki:

Algorytm	Liczba liter	Liczba blanków	Średni czas [ms]
dict	7	0	0.24
dict	7	1	4.58
dict	7	2	180.2
trie	7	0	0.22
trie	7	1	15.8
trie	7	2	1103.5

Wniosek? W dość zaawansowany sposób pokazaliśmy, że strzelanie z armaty do much niekoniecznie ma sens. Algorytm oparty na drzewie trie jest minimalnie szybszy bez blanków, natomiast jeżeli tylko pokazują się blanki, okazuje się dużo wolniejszy. Z lenistwa nie przetestowałem już prędkości dla innych liczb liter, może ktoś się kiedyś pokusi... Pewnie dałoby się też wprowadzić jakieś optymalizacje tu i ówdzie - zabrakło mi jednak rozpędu na dalsze zabawy.

Aha, oczywiście plik .pkl dla algorytmu trie jest ponaddwukrotnie większy (dict: 100MB, trie: 224MB) co technicznie podwaja wielkość armaty.

https://xpil.eu/d4gd