Do stu lat pewnie nie dożyję, ale do czterdziestu sześciu właśnie mi się udało. Z tej to okazji dziś garść kompletnie bezużytecznych i w dodatku bardzo nudnych faktów o liczbie 46.
Zaczniemy od tego, że 46 jest liczbą centralnie trójkątną. Szóstą z kolei. Poprzednie to 1, 4, 10, 19 i 31. Następna to dopiero 64 i potem jeszcze ewentualnie 85. Do 106, jak już nadmieniłem, raczej nie dociągnę.
Cóż to takiego, liczba centralnie trójkątna?
Otóż stawiamy kropkę. Liczymy kropkę. Kropka jest jedna, a więc tyle też wynosi wartość pierwszej liczby centralnie trójkątnej. Bo tak.
Następnie rysujemy dookoła tej kropki trójkąt i stawiamy w każdym jego rogu kropkę. Razem mamy więc 4 kropki.
Następnie rysujemy dookoła tego trójkąta większy trójkąt i stawiamy kropki w każdym wierzchołku oraz po jednej pośrodku każdego boku. Liczymy wszystkie narysowane dotychczas kropki. Jest 10?
No to teraz wokół tego trójkąta rysujemy jeszcze jeden, większy od tamtego, i teraz oprócz wierzchołków na każdym boku rysujemy dwie kropki.
Na bokach kolejnego trójkąta rysujemy już po trzy kropki. Efekt będzie taki:
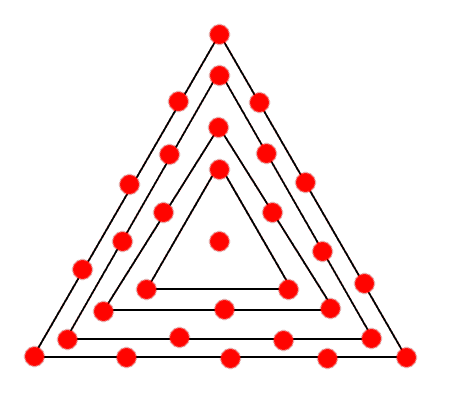
Tu mamy już 31 kropek, a po dorysowaniu kolejnego trójkąta uzyskamy ich równo 46.
46 jest też czwartą z kolei liczbą dziewięciokątną.
(nie wiem czy tak się tłumaczy angielskie nonagonal number ale przyjmę z lenistwa, że tak)
Liczby dziewięciokątne buduje się też z kropek, ale nie na trójkątach tylko na dziewięciokątach. Dokładnie na ich wierzchołkach:
Za pierwszą liczbę dziewięciokątną przyjmuje się 1. Bo tak.
Druga to 9 czyli liczba wierzchołków - uwaga, niespodzianka - dziewięciokąta.
Trzecia powstaje poprzez dorysowanie do dziewięciokąta drugiego, większego, który współdzieli z mniejszym jeden wierzchołek oraz fragmenty dwóch boków:

Powstały w ten sposób 24 kropki. Powtarzając procedurę dostaniemy 46 kropek a potem jeszcze 75 i 111. I tak dalej.
46 jest liczbą kongruentną, co oznacza, że istnieje trójkąt prostokątny o polu powierzchni 46, którego wszystkie trzy boki są liczbami wymiernymi (nie chciało mi się jednak takiego trójkąta szukać).
Najlepsze jednak przed nami: otóż 46 jest dziewiątą z kolei liczbą... naleśnikową!
N-ta liczba naleśnikowa mówi nam na ile maksymalnie kawałków możemy podzielić naleśnik za pomocą N prostych cięć. Okazuje się, że przy dziewięciu cięciach możemy uzyskać maksymalnie 46 kawałków naleśnika.
Historycznie w 46 roku nic ciekawego się nie wydarzyło. Urodził się Plutarch, a populacja Imperium Rzymskiego przekroczyła sześć milionów obywateli.
Niech żyję!
Sto sześć lat (co najmniej) i zdrówka
Zdrowia, szczęścia, radości z mnożenia i dzielenia, dodawania i odejmowania, a jakże i potęgowania! Niech się liczą liczby nie tylko naleśnikowe i inne owe, szczęśliwe i nieurojone one. Dużych i małych radości, świetnych książek, dobrych ludzi, uśmiechu, podróży małych i dużych. Co ja będę kruszyć czcionkę, szczęścia.
Historycznie w 46 roku nic się nie zdarzyło.
Czyżby, a proszę zajrzeć za kulisy, rok 46 p.n.e – w tym roku wprowadzono kalendarz juliański czyli wynaleziono rok przestępny.
Patrz tu: https://en.wikipedia.org/wiki/46_BC
Czyli luty z 29 dniami.
A przypomnę, że Rossini urodził się 29 lutego.
Czyli jakby nie było kalendarza juliańskiego i jego następców, to Rossini by się nie urodził.
To co wart by był ten świat???
Życzę na początek kolejnych 46 lat.
non-agonal kojarzy mi się trochę inaczej. Poza tym ciocia Wikipedia składa ci życzenia, albowiem: „Juliusz Cezar zdecydował, że od 1 stycznia następnego roku będzie obowiązywał nowy kalendarz juliański. Aby zniwelować różnicę między starym a nowym kalendarzem, rok 46 p.n.e. został przedłużony do 445 dni, przez co zyskał sobie miano „annus confusionis” – roku bałaganu. Był to najdłuższy rok w historii.”
Rok bałaganu… to by się mniej więcej zgadzało z obecną sytuacją 😉
Niech żyjesz!
Może źle odczytujesz nazwę liczby po angielsku? Może nonagonal trzeba czytać non-agonal? Albo non agonal wręcz?
W sam raz na urodziny.
„Okazuje się, że przy dziewięciu cięciach możemy uzyskać maksymalnie 46 kawałków naleśnika”
E tam, zwinięty (z serem) w rulonik, albo na pół złożony i jeszcze raz na pół (z dżemem) da się podzielić na dużo więcej części – idzie już w setki. Ale jeśli zrezygnujemy z prostych cięć, to z uzyskanych kawałków jednego naleśnika możemy złożyć dwa takie same, jak ten, przed pocięciem. To znaczy, że czeka cię jeszcze drugie 46 lat (dokładnie), czego nie życzę, bo końcówka w takim wieku zazwyczaj nie bywa przyjemna…
Końcówka, obawiam się, w żadnym wieku nie jest przyjemna 🙂