Jak każdego zdrowego faceta po czterdziestce, od czasu do czasu łapie mnie straszna chętka na napisanie jakiegoś interesującego algorytmu na losowy spacer na dwuwymiarowej płaszczyźnie. Starzy (w sensie stażu, niekoniecznie biologicznym) Czytelnicy blogu być może kojarzą te wpisy: 1, 2, 3, 4 - jak widać wytyczanie ścieżek na płaszczyźnie wraca do mnie jak bumerang.
Ostatnio znów mnie naszło - tym razem z głupia frant spróbowałem czegoś następującego:
- Startujemy w puncie (0,0), z azymutem 2°.
- Robimy krok.
- Znajdujemy kolejną liczbę pierwszą po dwójce (czyli 3)
- Zakręcamy więc o 3° - teraz nasz azymut to 5°
- Robimy kolejny krok.
- Po trójce kolejna liczba pierwsza to 5
- Zakręcamy więc o 5° czyli nasz obecny azymut to 10°
- Robimy krok
I tak dalej, przez, dajmy na to, 100 albo 1000 albo 100000 kroków. Jak będzie wyglądać nasza ścieżka?
Okazuje się, że całkiem inaczej od wszystkich losowych ścieżek, które do tej pory udało mi się wypocić!
Jeżeli ograniczymy się do 50 pierwszych kroków, wynik jest niezbyt imponujący:
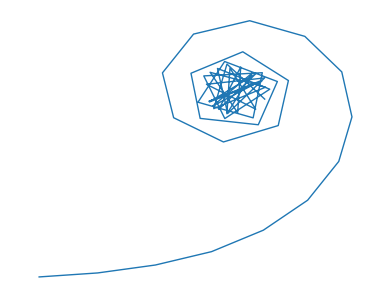
Ale już zwiększenie licznika do stu kroków daje intrygujący efekt:
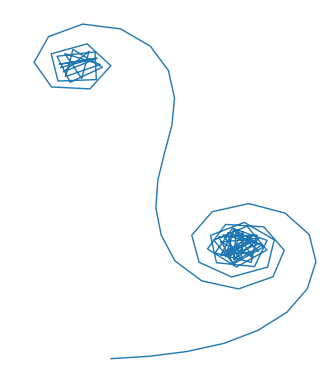
Co się tutaj wydarzyło?
W środku spiralki jest taka gęstwina, bo nasze zakręty robią się bardzo ostre (o więcej niż kąt prosty) więc w zasadzie drepczemy w miejscu (technicznie nie w miejscu tylko w niewielkim obszarze). Ale ponieważ koło jest kołem i zakręt w pewnym momencie przekracza 270 stopni - czyli kąt prosty wywrócony na lewą stronę - zabazgrawszy spiralkę "uciekamy" od niej prostującym się kawałkiem krzywej. Po dotarciu do 360 stopni (to ten kawałek w miarę prostej trasy między dwiema spiralkami) sytuacja powtarza się i produkujemy kolejną spiralkę. A co jeżeli zwiększymy teraz liczbę kroków do 1000?

To już wygląda całkiem ciekawie. Dość losowo a jednocześnie jakby powtarzalnie. Fraktal to to nie jest, ale i tak mi się podoba.
Dalsze zwiększanie liczby kroków nie daje już zbyt oszałamiających efektów. Na przykład dla 100000 dostajemy takie coś:

Owszem, fajne, ale można by to jakoś podrasować.
Co by tu...
Zacznijmy od tego, że dobrze byłoby trochę złagodzić te ostre kanty na zakrętach.
Tutaj oryginalny kod:
import matplotlib.pyplot as plt
from math import radians, sin, cos
from sympy import nextprime
xlist, ylist = [0.0], [0.0]
x, y = 0.0, 0.0
angle_degrees = 2
angle_radians = radians(angle_degrees)
lw = '0.5' # line width
for n in range(500):
angle_degrees = nextprime(angle_degrees)
angle_radians += radians(angle_degrees)
x += cos(angle_radians)
y += sin(angle_radians)
xlist.append(x)
ylist.append(y)
plt.xticks([])
plt.yticks([])
plt.box(False)
plt.plot(xlist, ylist, linewidth=lw)
plt.show()
... a tutaj drobna zmiana, dzięki której zakręty stają się bardziej łagodne (kosztem jednakowoż konieczności zwiększenia liczby kroków):
import matplotlib.pyplot as plt
from math import radians, sin, cos
from sympy import nextprime
xlist, ylist = [0.0], [0.0]
x, y = 0.0, 0.0
angle_degrees = 2
angle_radians = radians(angle_degrees)
lw = '0.5' # line width
for n in range(10000):
angle_degrees = nextprime(angle_degrees)
angle_radians += radians(angle_degrees/20)
x += cos(angle_radians)
y += sin(angle_radians)
xlist.append(x)
ylist.append(y)
plt.xticks([])
plt.yticks([])
plt.box(False)
plt.plot(xlist, ylist, linewidth=lw)
plt.show()
Wynik:
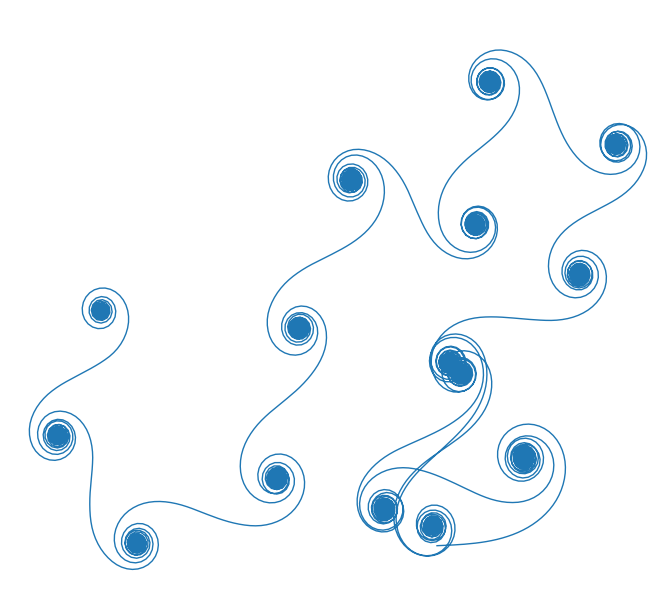
No dobra. Co by tu jeszcze...
Jest jakby trochę monochromatycznie. Spróbujmy dodać kolorków. Tylko jak?
Zmodyfikujemy nasz kod tak, żeby linia zmieniała kolor za każdym razem kiedy natrafimy na liczbę pierwszą bliźniaczą:
import matplotlib.pyplot as plt
from math import radians, sin, cos
from sympy import nextprime
from itertools import cycle
xlist, ylist = [0.0], [0.0]
x, y = 0.0, 0.0
angle_degrees = 2
angle_radians = radians(angle_degrees)
lw = '0.5' # line width
colors = cycle('bgrcmk')
for n in range(10000):
previous_angle = angle_degrees
angle_degrees = nextprime(angle_degrees)
if (angle_degrees-previous_angle == 2):
plt.plot(xlist, ylist, linewidth=lw, c = next(colors))
xlist, ylist=[x],[y]
angle_radians += radians(angle_degrees/20)
x += cos(angle_radians)
y += sin(angle_radians)
xlist.append(x)
ylist.append(y)
plt.xticks([])
plt.yticks([])
plt.box(False)
plt.show()
Wynik:

Nie podoba mi się. Kolorki w środku spiral nakładają się na siebie, nadal jest nudno. Co by tu zamiast tego...
A gdyby tak zmieniać kierunek, w którym zakręcamy, na przeciwny za każdym razem kiedy trafimy na liczbę pierwszą bliźniaczą?
Hmmm.
import matplotlib.pyplot as plt
from math import radians, sin, cos
from sympy import nextprime
xlist, ylist = [0.0], [0.0]
x, y = 0.0, 0.0
angle_degrees = 2
angle_radians = radians(angle_degrees)
lw = '0.5' # line width
flip = 1
for n in range(10000):
previous_angle = angle_degrees
angle_degrees = nextprime(angle_degrees)
if (angle_degrees-previous_angle == 2):
flip *= -1
angle_radians += flip * radians(angle_degrees/20)
x += cos(angle_radians)
y += sin(angle_radians)
xlist.append(x)
ylist.append(y)
plt.xticks([])
plt.yticks([])
plt.box(False)
plt.plot(xlist, ylist, linewidth=lw)
plt.show()
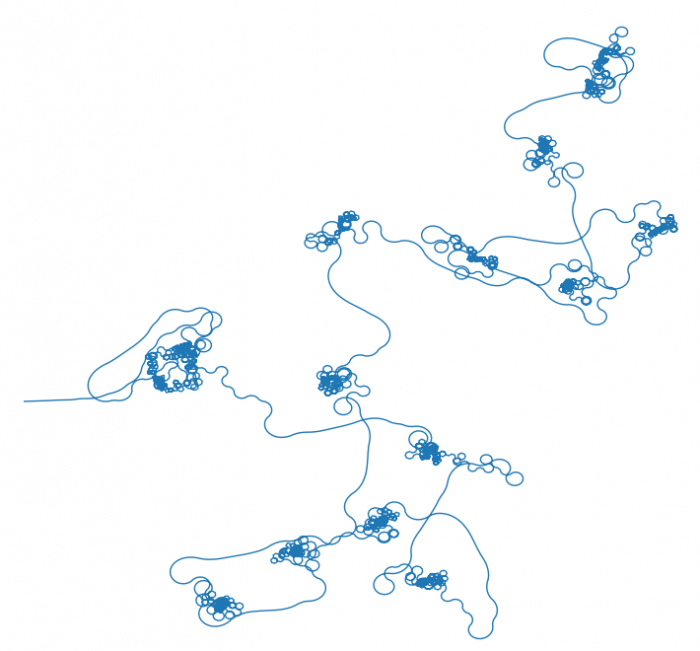
I to już jest jakościowa zmiana - widać wyraźnie miejsca, w których ścieżka zakręca raz w jedną, raz w drugą stronę bez zapadania się w "studnię grawitacyjną" kolejnej spiralki.
Co by tu jeszcze...
Przywróćmy pomysł z kolorowaniem (z poprzedniej wersji skryptu) zachowując jednocześnie pomysł z zakręcaniem:
import matplotlib.pyplot as plt
from math import radians, sin, cos
from sympy import nextprime
from itertools import cycle
xlist, ylist = [0.0], [0.0]
x, y = 0.0, 0.0
angle_degrees = 2
angle_radians = radians(angle_degrees)
lw = '0.5' # line width
flip = 1
colors = cycle('bgrcmk')
for n in range(10000):
previous_angle = angle_degrees
angle_degrees = nextprime(angle_degrees)
if (angle_degrees-previous_angle == 2):
flip *= -1
plt.plot(xlist, ylist, linewidth=lw, c = next(colors))
xlist, ylist=[x],[y]
angle_radians += flip * radians(angle_degrees/20)
x += cos(angle_radians)
y += sin(angle_radians)
xlist.append(x)
ylist.append(y)
plt.xticks([])
plt.yticks([])
plt.box(False)
plt.show()
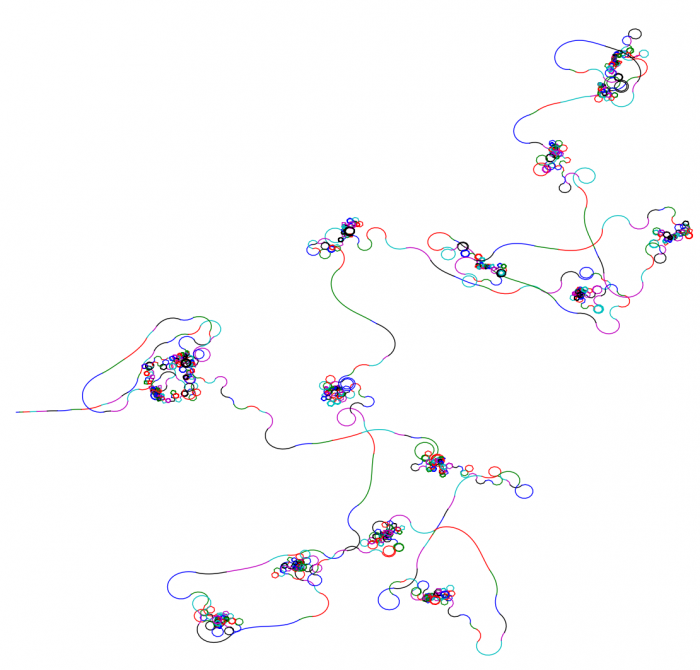
Żeby za każdym razem skrypt generował nam nieco inną ścieżkę, można dodać odrobinę losowości:
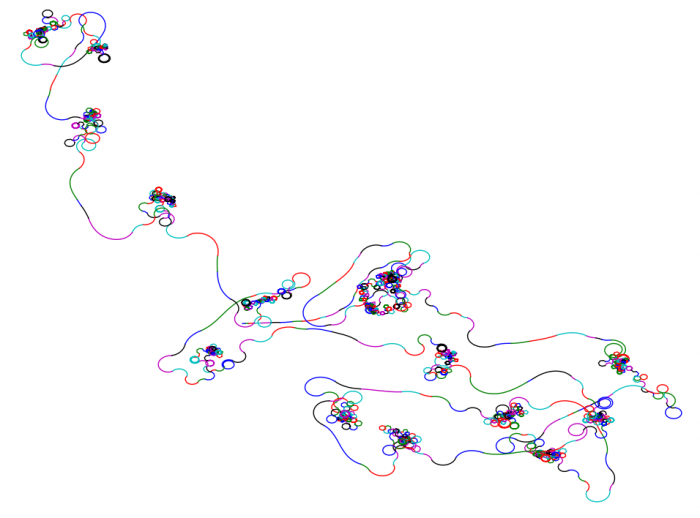
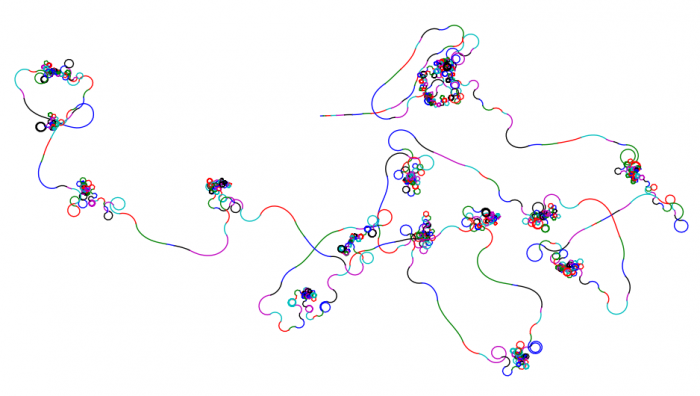
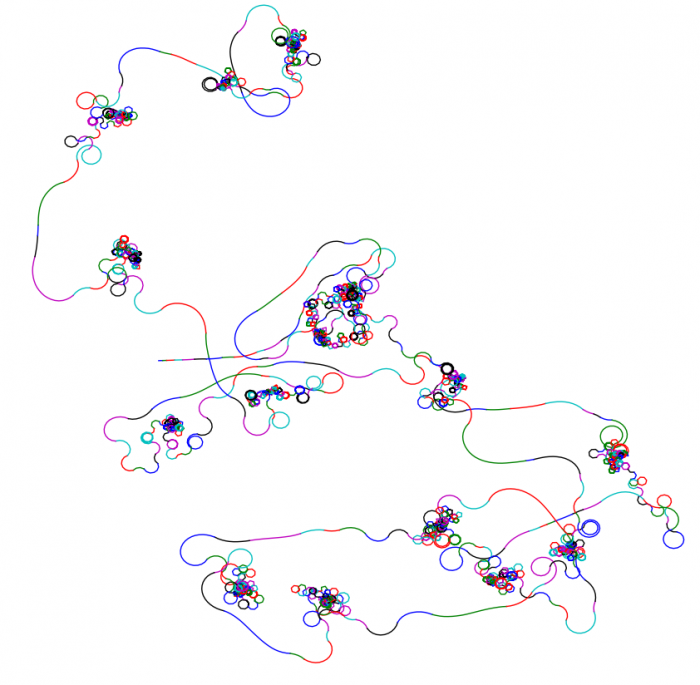
import matplotlib.pyplot as plt
from math import radians, sin, cos
from sympy import nextprime
from itertools import cycle
from random import random
xlist, ylist = [0.0], [0.0]
x, y = 0.0, 0.0
angle_degrees = 2
angle_radians = radians(angle_degrees)
lw = '0.5' # line width
flip = 1
colors = cycle('bgrcmk')
for n in range(10000):
previous_angle = angle_degrees
angle_degrees = nextprime(angle_degrees)
if (angle_degrees-previous_angle == 2):
flip *= -1
plt.plot(xlist, ylist, linewidth=lw, c = next(colors))
xlist, ylist=[x],[y]
angle_radians += flip * radians(angle_degrees/20) * (1 + random()/1000.0)
x += cos(angle_radians)
y += sin(angle_radians)
xlist.append(x)
ylist.append(y)
plt.xticks([])
plt.yticks([])
plt.box(False)
plt.show()
Temat można ciągnąć w zasadzie bez końca, ale chwilowo mam dość. Jestem jednak przekonany, że losowe spacery jeszcze się tutaj pojawią nie raz.
To jest spaghetti code.
Zgadza się – a zatem smacznego! 🙂