Na ogół nie cytuję innych blogerów (zbyt wiele mam bowiem ważkich i nie cierpiących zwłoki własnych treści, żeby jeszcze zajmować się cudzymi), jednak dzisiejszy obrazek na xkcd.com rozmiękczył mnie całkowicie:
Dla niewładających językiem Szekspira, tłumaczę:
Na środku, dużymi literami: HIPOTEZY GOLDBACHA
Od góry, po kolei w lewo:
SŁABA: każda liczba nieparzysta większa niż 5 jest sumą trzech liczb pierwszych.
BARDZO SŁABA: każda liczba większa od 7 jest sumą dwóch innych liczb.
EKSTREMALNIE SŁABA: liczby ciągle rosną
Od góry, po kolei w prawo:
SILNA: każda liczba parzysta większa od 2 jest sumą dwóch liczb pierwszych.
BARDZO SILNA: każda liczba nieparzysta jest pierwsza.
EKSTREMALNIE SILNA: nie ma liczb większych od 7.
Do tego dochodzi jeszcze opis obrazka (tzw. "alt text" czyli tekst pojawiający się po najechaniu na obrazek kursorem myszy, a także tekst, który pojawi się w miejscu obrazka w przypadku, kiedy przeglądarka nie wyświetla obrazków): "The weak twin primes conjecture states that there are infinitely many pairs of primes. The strong twin primes conjecture states that every prime p has a twin prime (p+2), although (p+2) may not look prime at first. The tautological prime conjecture states that the tautological prime conjecture is true."
Po naszemu: "Słaba hipoteza o liczbach pierwszych bliźniaczych mówi, że istnieje nieskończenie wiele par liczb pierwszych. Silna hipoteza o liczbach pierwszych bliźniaczych mówi, że każda liczba pierwsza p ma bliźniaczą liczbę pierwszą (p+2), chociaż (p+2) może na początku nie wyglądać zbyt pierwszo. Tautologiczna hipoteza o liczbach pierwszych mówi, że tautologiczna hipoteza o liczbach pierwszych jest prawdziwa."
Jak dla mnie to ten facet, który rysuje XKCD.com, powinien dostać nagrodę Nobla w dziedzinie edukacyjno-humorystycznej.
Więcej śmiechostek:
- 83 powody do uśmiechu czyli co bawiło mnie w styczniu 2022 roku
- Październikowe podśmiechujki
- Ma być śmiesznie? No to będzie śmiesznie. Lista podśmiechujek z kwietnia 2024.
- 54 powody do uśmiechu, czyli co śmieszyło mnie w maju 2019
- 78 powodów do uśmiechu czyli co bawiło mnie w styczniu 2020
- Co śmieszyło mnie w kwietniu 2019
- 115 powodów do uśmiechu, czyli z czego śmiałem się w maju 2024
- 62 powody do uśmiechu, czyli co śmieszyło mnie w styczniu 2019 roku
- 85 powodów do uśmiechu, czyli co poprawiało mi humor w marcu 2022
- 82 powody do uśmiechu, czyli co bawiło mnie w grudniu 2021
- Co śmieszyło mnie w lipcu 2019
- Endorfinki endorfinki dla chłopczyka i dziewczynki, czyli co śmieszyło mnie w lutym 2019 roku
- 35 powodów do uśmiechu, czyli co śmieszyło mnie w listopadzie 2019
- 149 powodów do uśmiechu czyli co bawiło mnie w maju 2020
- 98 powodów do uśmiechu, czyli październikowe podśmiechujki
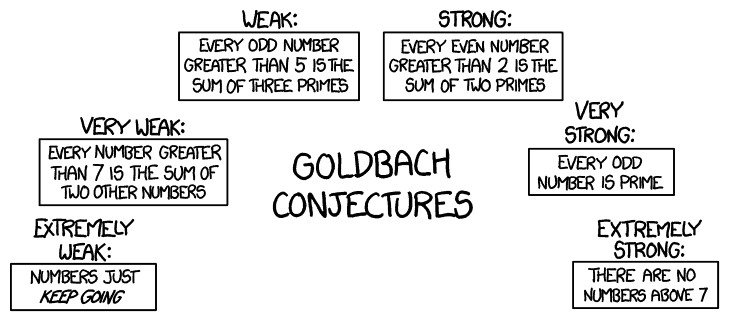
Ja jak zwykle tego typu wpisów NIE ROZUMIE. Ale zgadzam się z tym: „EKSTREMALNIE SILNA: nie ma liczb większych od 7”. ósemka to dwa zera, dziewiątka to odwrócona szóstka a dziesiątka to wiadomo: 1 + 0. Reszta to różne kompilacje mniejszych numerów.
Nie wydaje mi się, żeby o to chodziło autorowi, ale doceniam oryginalne podejście :]
Ta ekstremalnie silna hipoteza jest dość łatwa do udowodnienia. Wystarczy na płaszczyźnie umieścić wszystkie liczby, znaleźć 7 i umieścić ją na płaszczyźnie wyższej. No i ewentualnie dać ją większą czcionką by rozwiać wszelkie wątpliwości.