W zagadce pytam o to jaka jest najdłuższa minimalna drabinka liczb pierwszych trzy- i czterocyfrowych, przy czym drabinkę określamy jako przejście od jednej liczby do drugiej w taki sposób, aby wszystkie liczby pośrednie również były pierwsze, a każda różniła się od poprzedniej dokładnie jedną cyfrą.
Szukanie najkrótszych drabinek to zagadnienie nie do końca banalne. Można próbować zbudować drzewo startujące od liczby pierwszej a następnie szukać najdłuższego rozgałęzienia - i potem kolejne drzewo startujące od innej liczby pierwszej i tak dalej. Zbudowawszy las takich drzew dla każdej liczby początkowej znajdziemy w końcu najdłuższe rozgałęzienie.
Można zamiast tego zbudować graf z wierzchołkami będącymi liczbami pierwszymi o zadanej długości, połączyć ze sobą te, które różnią się jedną cyfrą a następnie znaleźć średnicę tego grafu.
Taki graf dla liczb dwucyfrowych wygląda tak:
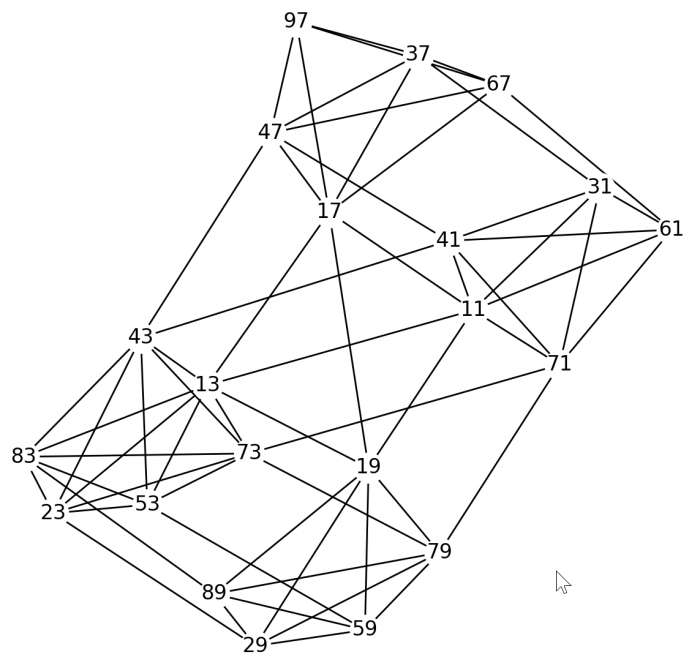
A dla trzycyfrowych - tak:

Dla cztero-i-więcej-cyfrowych grafy robią się już nieczytelne:
Szukanie średnicy grafu to zadanie obliczeniowo dość złożone; praktycy definiują wpawdzie pseudośrednicę grafu jako średnicę przybliżoną: wybieramy jakiś wierzchołek, mierzymy odległość do wszystkich innych wierzchołków, wybieramy ten z największą odległością, operację powtarzamy N razy. Przy odpowiednio dobranym N mamy sporą *szansę* znaleźć faktyczną średnicę, ale spróbujmy zrobić to porządnie, czyli na pewniaka. Zabiorę się za zagadnienie za pomocą Pythona. Grafy nie są czymś nowym i mamy tutaj do dyspozycji całkiem sporo bibliotek. Ja zdecydowałem się na networkx.
Biblioteka ta ma wbudowaną opcję liczenia średnicy grafu, więc od razu po zbudowaniu połączeń między liczbami mogę sprawdzić jakie jest najdłuższe z nich, za pomocą funkcji diameter. Niestety funkcja ta nie zwraca najdłuższych ścieżek - mówi tylko jaka jest ich długość, czyli trzeba sobie samemu dopisać kawałek kodu, który takie ścieżki znajduje.
Ponadto zanim zaczniemy w ogóle szukać średnicy grafu, trzeba najpierw sprawdzić czy graf jest spójny czy nie (jak za chwilę zobaczymy, przy większych grafach niektóre liczby będą "oddzielone" od reszty). Na szczęście networkx ma tu również odpowiednie narzędzia.
Poniższy kod dla liczb trzycyfrowych wykonuje się praktycznie natychmiastowo; dla czterech cyfr trzeba poczekać około 2.5 sekund.
from sympy import isprime
import networkx as nx
# import matplotlib.pyplot as plt # rysowanie grafów
from datetime import datetime as dt
liczba_cyfr = 6
print(f'{dt.now()}: Generowanie listy liczb pierwszych {liczba_cyfr}-cyfrowych')
pierwsze = [n for n in range(
10**(liczba_cyfr-1), 10**liczba_cyfr) if isprime(n)]
print(f'{dt.now()}: Wygenerowano listę {len(pierwsze)} liczb')
G = nx.Graph()
print(f'{dt.now()}: Dodawanie wierzchołków grafu')
for p in pierwsze:
G.add_node(p)
print(f'{dt.now()}: Generowanie połączeń')
for nn in G.nodes:
liczba = str(nn)
for pozycjacyfry in range(len(liczba)):
for cyfra in range(10):
kandydat = liczba[:pozycjacyfry]+str(cyfra)+liczba[pozycjacyfry+1:]
if(kandydat != liczba and kandydat[0] != '0' and isprime(int(kandydat))):
G.add_edge(nn, int(kandydat))
print(f'{dt.now()}: Liczba połączeń w grafie: {len(list(G.edges))}, sprawdzanie spójności grafu')
największy_podgraf = 0
if nx.is_connected(G):
print(f'{dt.now()}: Graf jest spójny')
else:
print(f'{dt.now()}: Graf jest niespójny. Szukanie największego podgrafu')
cc = nx.connected_components(G)
for c in cc:
if(len(c) > największy_podgraf):
największy_podgraf = len(c)
G = G.subgraph(c).copy()
print(f'{dt.now()}: Znaleziono największy podgraf ({len(G.nodes)} wierzchołków, {len(G.edges)} połączeń)')
print(f'{dt.now()}: Wyliczanie średnicy')
d = nx.diameter(G)
długość_ścieżki = d + 1
print(f'{dt.now()}: Średnica: {d}, szukanie drabinek {długość_ścieżki}-elementowych')
for bieżący_wierzchołek in list(G.nodes()):
if(nx.eccentricity(G, bieżący_wierzchołek) == d):
for wierzchołek in list(G.nodes()):
ścieżka = nx.shortest_path(
G, bieżący_wierzchołek, wierzchołek)
if(len(ścieżka) == długość_ścieżki):
print(f'{dt.now()}: Drabinka: {ścieżka}')
# rysowanie grafów:
# nx.draw(G, with_labels=True, node_shape='o', font_size=7, edge_color='gray', node_color='white', width= 0.5)
# plt.show()
Dla trzycyfrowych, powyższy kod wypluwa:
2022-05-30 14:23:38.859459: Generowanie listy liczb pierwszych 3-cyfrowych
2022-05-30 14:23:38.861459: Wygenerowano listę 143 liczb
2022-05-30 14:23:38.861459: Dodawanie wierzchołków grafu
2022-05-30 14:23:38.861459: Generowanie połączeń
2022-05-30 14:23:38.869472: Liczba połączeń w grafie: 517, sprawdzanie spójności grafu
2022-05-30 14:23:38.871460: Graf jest spójny
2022-05-30 14:23:38.871460: Wyliczanie średnicy
2022-05-30 14:23:38.895458: Średnica: 6, szukanie drabinek 7-elementowych
2022-05-30 14:23:38.906461: Drabinka: [389, 349, 449, 409, 401, 461, 761]
2022-05-30 14:23:38.918460: Drabinka: [761, 461, 401, 409, 449, 349, 389]Dla czterocyfrowych:
2022-05-30 14:18:14.208583: Generowanie listy liczb pierwszych 4-cyfrowych
2022-05-30 14:18:14.215602: Wygenerowano listę 1061 liczb
2022-05-30 14:18:14.216443: Dodawanie wierzchołków grafu
2022-05-30 14:18:14.218466: Generowanie połączeń
2022-05-30 14:18:14.296452: Liczba połączeń w grafie: 4107, sprawdzanie spójności grafu
2022-05-30 14:18:14.300452: Graf jest spójny
2022-05-30 14:18:14.300452: Wyliczanie średnicy
2022-05-30 14:18:15.558450: Średnica: 8, szukanie drabinek 9-elementowych
2022-05-30 14:18:15.856453: Drabinka: [2441, 2447, 8447, 8147, 5147, 5197, 6197, 6199, 9199]
2022-05-30 14:18:16.173449: Drabinka: [4391, 4091, 4001, 4003, 2003, 2803, 6803, 6883, 6983]
2022-05-30 14:18:16.252466: Drabinka: [4651, 4051, 4001, 4003, 2003, 2803, 6803, 6883, 6983]
2022-05-30 14:18:16.599744: Drabinka: [6983, 6883, 6803, 2803, 2003, 4003, 4001, 4091, 4391]
2022-05-30 14:18:16.602745: Drabinka: [6983, 6883, 6803, 2803, 2003, 4003, 4001, 4051, 4651]
2022-05-30 14:18:16.624729: Drabinka: [6983, 6883, 6833, 6133, 6131, 6151, 1151, 1951, 8951]
2022-05-30 14:18:16.909745: Drabinka: [8951, 1951, 1151, 6151, 6131, 6133, 6833, 6883, 6983]
2022-05-30 14:18:16.967744: Drabinka: [9199, 6199, 6197, 5197, 5147, 8147, 8447, 2447, 2441]Zrobiłem też eksperyment dla liczb pięciocyfrowych i tu już musiałem poczekać na wynik około czterech minut:
2022-05-30 14:18:24.119264: Generowanie listy liczb pierwszych 5-cyfrowych
2022-05-30 14:18:24.228445: Wygenerowano listę 8363 liczb
2022-05-30 14:18:24.229447: Dodawanie wierzchołków grafu
2022-05-30 14:18:24.236449: Generowanie połączeń
2022-05-30 14:18:25.369463: Liczba połączeń w grafie: 33393, sprawdzanie spójności grafu
2022-05-30 14:18:25.424450: Graf jest spójny
2022-05-30 14:18:25.425449: Wyliczanie średnicy
2022-05-30 14:20:21.659944: Średnica: 10, szukanie drabinek 11-elementowych
2022-05-30 14:21:59.672745: Drabinka: [88259, 48259, 45259, 45959, 41959, 41969, 91969, 91961, 99961, 99761, 99721]
2022-05-30 14:22:15.375976: Drabinka: [99721, 99761, 99961, 91961, 91969, 41969, 41959, 45959, 45259, 48259, 88259]Jak widać biblioteka networkx potrzebowała minuty i 45 sekund na samo wyliczenie średnicy grafu, kolejne dwie minuty zeszły na szukanie drabinek.
Przy liczbach sześciocyfrowych zaczęły się schody. Po pierwsze okazało się, że niektóre liczby nie są połączone z resztą grafu (jest ich dokładnie 6), a więc procedura szukania średnicy wywalała błąd i musiałem dodać sprawdzanie spójności + znajdowanie największego podgrafu. Po drugie - prędkość działania:
2022-05-30 14:28:39.371706: Generowanie listy liczb pierwszych 6-cyfrowych
2022-05-30 14:28:40.919928: Wygenerowano listę 68906 liczb
2022-05-30 14:28:40.920909: Dodawanie wierzchołków grafu
2022-05-30 14:28:40.993910: Generowanie połączeń
2022-05-30 14:28:56.290753: Liczba połączeń w grafie: 279563, sprawdzanie spójności grafu
2022-05-30 14:28:56.599774: Graf jest niespójny. Szukanie największego podgrafu
2022-05-30 14:28:58.905801: Znaleziono największy podgraf (68900 elementów)
2022-05-30 14:28:58.906802: Wyliczanie średnicyPrawie dwadzieścia sekund żeby w ogóle dotrzeć do momentu wyliczania średnicy. Potem - cisza. Zgrubne i na oko zrobione wyliczenia na podstawie czasów wykonania dla mniejszych grafów powiedziały mi, że na policzenie średnicy będę musiał poczekać około sześciu godzin. Czemu tak? Dla trzycyfrowych średnica policzyła się w ciągu 0.02 sekund, dla czterocyfrowych - w ciągu 1.25 sekund, a dla pięciocyfrowych w 167 sekund. Mnożnik wychodzi w okolicach między 50 a 130 - załóżmy pesymistycznie 130, 167*130 daje niecałe 22200 sekund czyli ciut ponad 6 godzin.
Nastawiłem się na cierpliwość, ale z ciekawości uruchomiłem też ten sam skrypt za pomocą pypy - do kroku z wyliczaniem średnicy dotarł w sześć sekund zamiast dwudziestu, a więc jakieś 3x szybciej. A nuż?
W "zwykłym" Pythonie zajęło to około 4 godzin:
2022-05-30 18:36:35.502552: Średnica: 12, szukanie drabinek 13-elementowychTymczasem PyPy:
2022-05-30 15:06:03.925246: Wyliczanie średnicy
2022-05-30 17:40:50.921883: Średnica: 12, szukanie drabinek 13-elementowychTylko 2 godziny 34 minuty. Nieźle. Po kolejnej godzinie i 25 minutach mamy też pierwszą drabinkę:
2022-05-30 19:05:27.621682: Drabinka: [440497, 410497, 410491, 410461, 414461, 404461, 704461, 704861, 704863, 704833, 705833, 905833, 995833]... a po kolejnych dwóch - drugą i ostatnią:
2022-05-30 21:04:44.451837: Drabinka: [995833, 905833, 705833, 704833, 704863, 704861, 704461, 404461, 414461, 410461, 410491, 410497, 440497]Na wersję siedmiocyfrową już się nie zdecydowałem 🙂
Jeżeli natomiast chcesz zobaczyć taką maksymalną najkrótszą drabinkę na własne oczy, trzeba na końcu powyższego skryptu dopisać:
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_shape='o', font_size=7, edge_color='gray', node_color='white', width= 0.5)
for ścieżka in ścieżki:
el = G.subgraph(ścieżka).edges
nl=G.subgraph(ścieżka).nodes
nx.draw_networkx_edges(G, pos, edgelist=el, edge_color='blue', width= 2)
nx.draw_networkx_nodes(G, pos, nodelist=nl, node_color='red')
plt.show()
Efekt dla liczb trzycyfrowych:
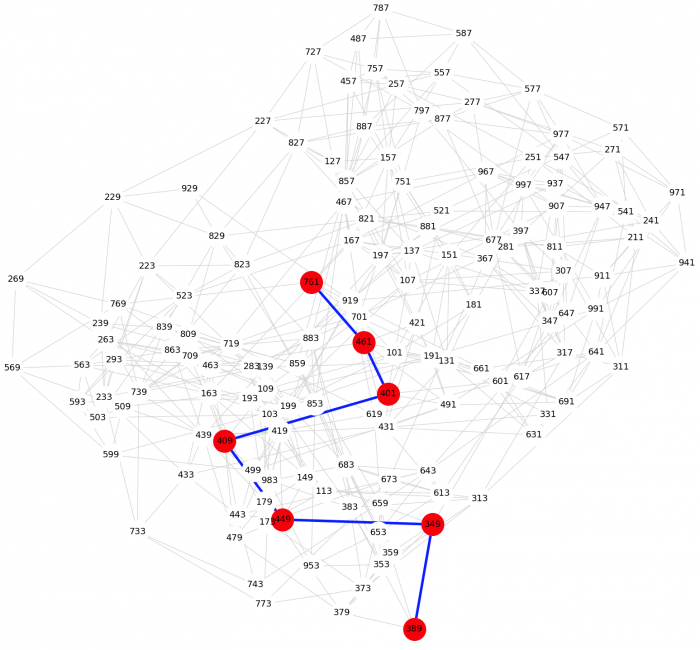
Zamiast spring_layout można oczywiście użyć innego algorytmu, na przykład Kamada-Kawai:
pos = nx.kamada_kawai_layout(G)
nx.draw(G, pos, with_labels=True, node_shape='o', font_size=7,
edge_color='lightgray', node_color='white', width=0.5)
for ścieżka in ścieżki:
el = G.subgraph(ścieżka).edges
nl = G.subgraph(ścieżka).nodes
nx.draw_networkx_edges(G, pos, edgelist=el, edge_color='blue', width=2)
nx.draw_networkx_nodes(G, pos, nodelist=nl, node_color='red')
plt.show()

Rozpaczliwa próba wizualizacji ścieżek dla czterocyfrowych:

A jak Wam poszło?
Niezbyt obficie tym razem. Tylko trzy zgłoszenia.
1Pierwszy odezwał sie Rozie i... pozamiatał, czapki z głów. Jego odpowiedź jest w zasadzie identyczna z moją powyżej z jedną "drobną" różnicą: zamiast skorzystać z gotowca w postaci biblioteki networkx, Rozie zamieścił kod klasy Graph bezpośrednio w skrypcie, podobnie jak implementację algorytmu Dijkstry. Szacuneczek. Rzecz jasna zaliczam i gratuluję wygranej.
2Nazajutrz swoje rozwiązanie przysłał Krzysiek i pozamiatał jeszcze bardziej 🙂 Przyznaję się bez bicia, że połowy jego kodu w Pythonie nie rozumiem (nie ma tam żadnych czarów... po prostu interesująco poukładane algorytmy), ale wyniki daje poprawne (jak widać poniżej). Zaliczam.
Wyniki dla N=4:
(4391, 6983) (4391, 4397, 4337, 6337, 6737, 6733, 6833, 6883, 6983)
(2441, 9199) (2441, 5441, 5443, 5413, 9413, 9403, 9103, 9109, 9199)
(4651, 6983) (4651, 4451, 4481, 4483, 4583, 7583, 7883, 6883, 6983)
(8951, 6983) (8951, 8971, 8171, 8161, 8861, 8863, 6863, 6883, 6983)
(6983, 4651) (6983, 6883, 6823, 6827, 5827, 5857, 5657, 4657, 4651)
(6983, 4391) (6983, 6883, 6823, 3823, 3821, 3121, 3191, 3391, 4391)
(6983, 8951) (6983, 6883, 6823, 1823, 1123, 1153, 1151, 1951, 8951)
(9199, 2441) (9199, 9109, 3109, 3169, 3469, 3467, 2467, 2447, 2441)
Dla N=5 (około 12 minut):
(99721, 88259) (99721, 99761, 93761, 93763, 93263, 96263, 96269, 96259, 76259, 78259, 88259)
(88259, 99721) (88259, 88289, 28289, 28789, 29789, 49789, 49787, 99787, 99767, 99761, 99721)
Potem było długo, długo nic, aż wreszcie...
3 ... za bary z zagadką wziął sie Waldek i przegrał srodze. Napisał sobie jakiś algorytm (ale nie pochwalił się szczegółami), który mu wypluł najdłuższą minimalną drabinkę trzycyfrową o długości siedem, a czterocyfrową - o długości 13. Nie zaliczam. Przy okazji podesłałem też Waldkowi (drogą e-mailową) najkrósze drabinki dla jego przykładowych par, czyli: [113, 613, 643, 443] oraz: [1117, 8117, 8317, 6317, 6397, 6197, 6199], ale znów bez odzewu...

No właśnie, miałem pisać to w F# ale okazałem się zbyt leniwy. Nie po raz pierwszy notabene.
@xpil „podesłałem też Waldkowi (drogą e-mailową) najkrósze drabinki”
1.
Dziwna sprawa – nie widzę ich. To już drugi raz, kiedy twoja wiadomość u mnie znika. Postanowiłem ją znaleźć za wszelką cenę. Jednak po pół godzinie szukania nic… W akcie desperacji wpisałem Thunderbirdowi w filtrze wiadomości „xpil” – i zdarzył się cud! W tym momencie twój e-mail pojawił się. Tak po prostu, zaczął być Nie mam pojęcia o co chodzi. Może ty masz jakiś pomysł?
2.
Po odczytaniu informacji o drabinkach (wreszcie) dosyć szybko znalazłem głupi błąd w jednej z moich funkcji. Chodzi o to, że wy użyliście gotowe biblioteki w których jest wszystko, o czym można pomarzyć (w końcu do tego służą), a ja je piszę od zera (dla sportu, bo lubię), stąd i błędy się zdarzają. Do wyliczeń zamiast Dijkstry użyłem sortowania topologicznego z koniecznymi przeróbkami.
3.
Przedstawienie ścieżki w grafach jest, jak pokazałeś mało ciekawe. Ja zamieniłem grafy na macierze. Dla wielocyfrowych liczb są one gigantyczne, ale po pomniejszeniu obrazka coś tam widać. Załączam obrazki dla dwóch i dla trzech cyfr. Dla drabinki trzycyfrowej 389->761 mój algorytm znalazł inne liczby: 389, 349, 149, 109, 101, 701, 761. Na rysunku jest ona zaznaczona na pomarańczowo (twoja jest niebieska).
Fajne z tymi macierzami. Są algorytmy oparte na mnożeniu / potęgowaniu macierzy przyległości, dające na wyjściu długość najkrótszej drabinki (nie trzeba kombinować ręcznie z zakręcaniem na jedynkach, „samo” się zakręca 🙂 ) – ale zabrakło mi już rozpędu (czytaj: rozumu) żeby się w nie wgryzać.
To nie własna implementacja klasy grafu i Dijkstry, tylko copy paste z netu. Czyli zaliczam to sobie na minus, nie plus, bo o istnieniu networkx zapomniałem. Ale ma to swoje dobre strony bo…
…wersji z networkx nie udało mi się uruchomić pod pypy – nie widzi modułu, a widzę, że jest trochę na bakier z virtualenv. Natomiast zwykłą jak najbardziej i różnica w działaniu była spora. Wersja z networkx w CPython była znacznie szybsza od „własnej”, więc jest potencjał.
Nie widać tego u Ciebie, ale u mnie długo trwało generowanie połączeń. Na tyle długo, że widać różnicę w czasie działania po bardzo wstępnej optymalizacji.
Średnica grafu wg networkx jest o 1 mniejsza od odpowiedzi w zadaniu. Detal, ale warto pamiętać.
Szacowanie czasu wykonania zgrubnie i z mnożnikiem, gdy podejrzewamy złożoność O(n^2) bywa zgubne. A skoro z każdego wierzchołka grafu sprawdzamy trasę do każdego innego, to właśnie takiej bym się spodziewał.
Zgodnie z treścią zadania możemy przerwać po znalezieniu pierwszej przykładowej ścieżki.
Last but not least – pisanie pod treść zadania jest wysoce nieoptymalne, jeśli chodzi o wydajność.
„Średnica grafu wg networkx jest o 1 mniejsza od odpowiedzi w zadaniu.” – no tak, bo średnicę mierzy się w krawędziach, a długość drabinki w wierzchołkach.
Co zaś do brakującego modułu w pypy, to trzeba zapuścić:
I zaraz potem:
Et voilà.
Dzięki za motywację i podpowiedź.
Tak naprawdę to
I dopiero po tym instalacja modułu.
U mnie zadziałało bez tych wszystkich venv*
Zadziałać to zadziała, tylko po co sobie śmiecić w systemie? 😉