Postawiona niedawno zagadka polega na znalezieniu ośmiu liczb pierwszych, które - umieszczone na wierzchołkach sześcianu - dadzą na każdej ścianie sumę identyczną do pozostałych.
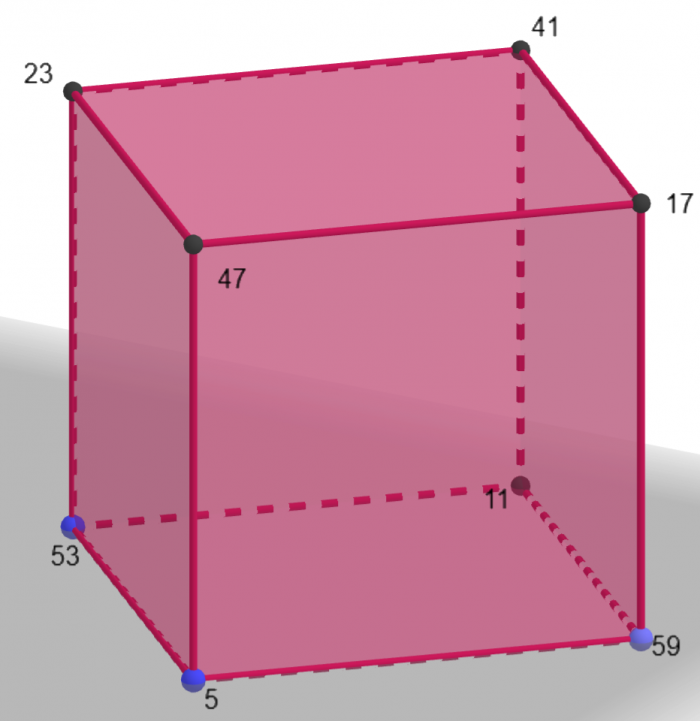
Wygląda to mniej więcej tak:
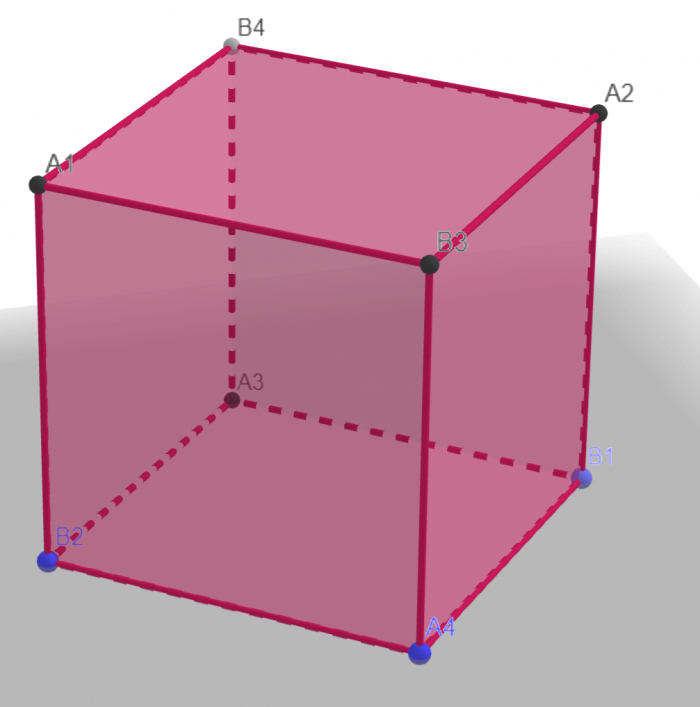
Oznaczenia wierzchołków są nieprzypadkowe - za chwilę okaże się dlaczego ponazywałem je akurat w ten sposób.
Spróbujmy na początek zapomnieć, że chodzi o liczby pierwsze i ponumerujmy wierzchołki po kolei, tj 1,2,3,4,5,6,7,8:
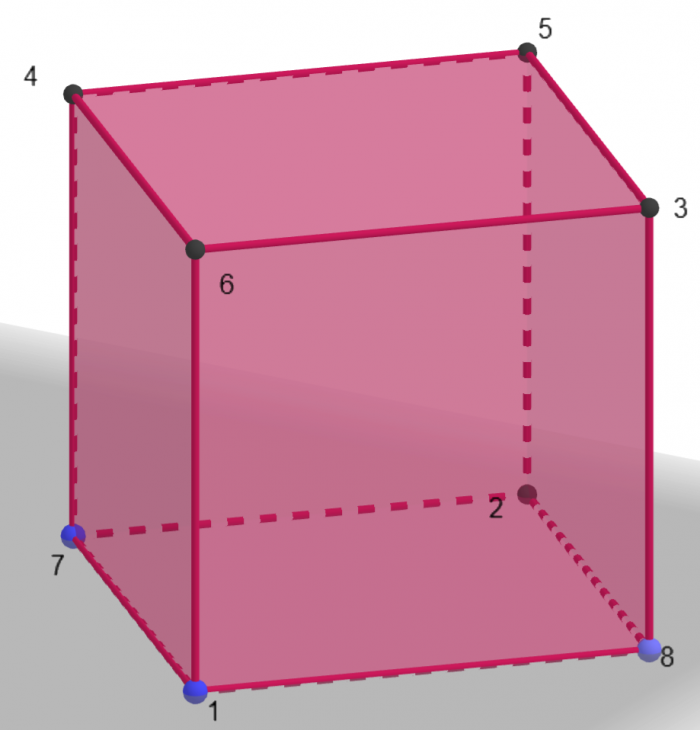
Skoro da się uzyskać jednakowe sumy na wszystkich ściankach za pomocą sekwencji 1-8, to od razu widać też, że powiększanie tej sekwencji (poprzez dodawanie lub mnożenie) też zadziała.
No dobrze. Wróćmy teraz do zadania. Szukamy liczb pierwszych takich, że:
A1+A2+B3+B4 = B1+B2+A3+A4 = A1+A3+B2+B4 = A2+A3+B1+B4 = A2+A4+B1+B3 = A1+A4+B2+B3 = X
, gdzie X jest sumą wspólną dla wszystkich sześciu ścian. Zapiszmy sobie powyższe jako:
A1+A2+B3+B4=X
B1+B2+A3+A4=X
A1+A3+B2+B4=X
A2+A3+B1+B4=X
A2+A4+B1+B3=X
A1+A4+B2+B3=X
Z powyższych sześciu równań można prosto dojść do:
A1-A2=B1-B2
A2-A3=B2-B3
A3-A4=B3-B4
Innymi słowy sekwencje liczb A1->A2->A3->A4 oraz B1->B2->B3->B4 są swoimi wzajemnymi wersjami przesuniętymi o pewną stałą. A więc istnieje takie T, że Ai=Bi+T dla każdego i między 1 a 4.
Można to też sobie rozrysować na dwa czworościany, jeden z wierzchołkami Ai a drugi z Bi:
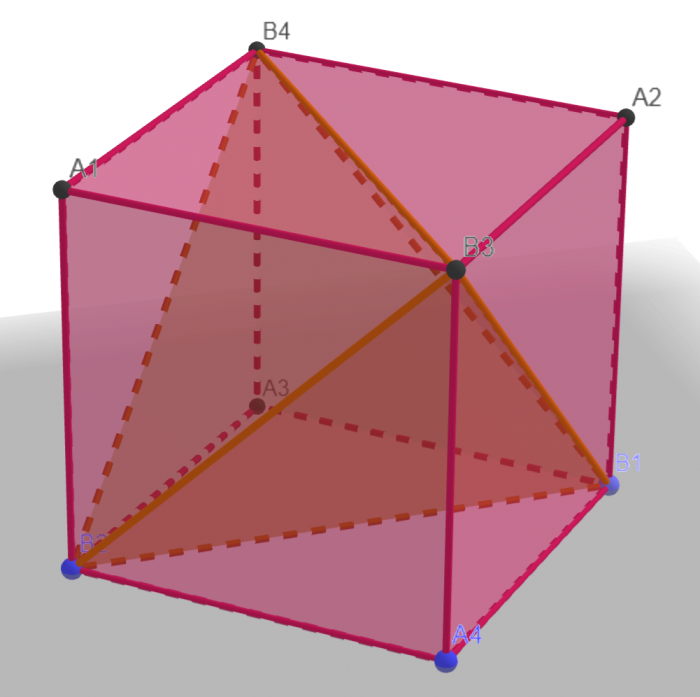
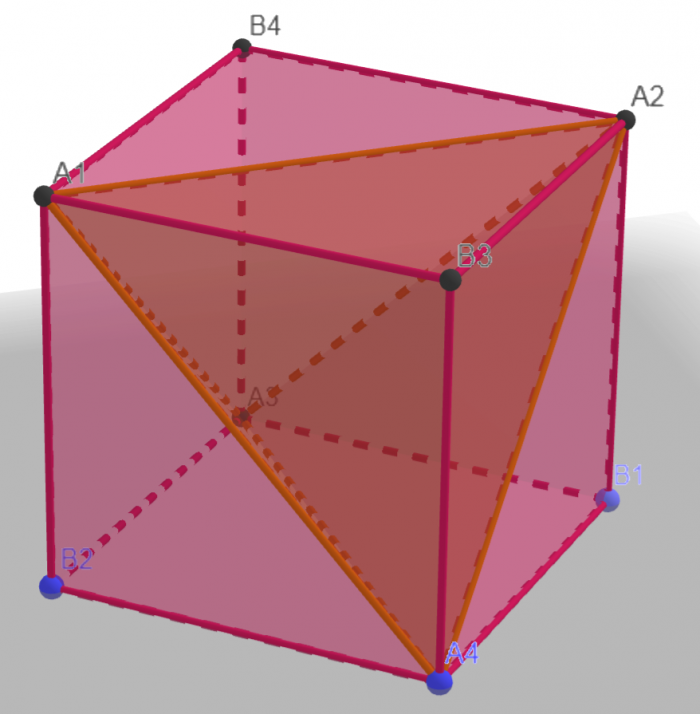
Każda ściana sześcianu zawiera dokładnie dwa wierzchołki każdego czworościanu, jeżeli więc zwiększymy wartości wierzchołków jednego z czworościanów o T, suma wszystkich ścian sześcianu zwiększy się o 2T. Na nasze: zamieniając 1,2,3,4,5,6,7,8 na, na przykład, 1,2,3,4,17,18,19,20 (czyli "odsuwając" pierwszą czwórkę od drugiej dowolnie daleko) nadal zachowamy identyczne sumy na wszystkich ścianach.
Biorąc pod uwagę powyższe rozważania wychodzi więc na to, że jeżeli znajdziemy dwa czteroelementowe arytmetyczne ciągi liczb (A1,A2,A3,A4) oraz (B1,B2,B3,B4) przesunięte względem siebie o dowolną stałą (no dobra, może nie dowolną - B1 powinno być większe od A4), dadzą one identyczne sumy ścian.
Tak więc zadanie sprowadza się do znalezienia czterech liczb pierwszych (A1,A2,A3,A4) tworzących ciąg arytmetyczny takich, że po dodaniu do nich pewnej stałej otrzymamy cztery inne liczby pierwsze (B1,B2,B3,B4).
Twierdzenie Green-Tao (udowodnione w 2004 roku) mówi, że ciągów arytmetycznych liczb pierwszych jest nieskończenie wiele, i to nie tylko czteroelementowych, ale również pięcio-, sześcio- i tak dalej aż do nieskończoności. Piszę o tym nieco szerzej tutaj:
Niestety Green-Tao to nie pokazuje jak szukać takich ciągów - udowadnia jedynie, że one istnieją. Skoro więc istnieje co najmniej jedna piątka liczb pierwszych tworzących ciąg geometryczny, to ta piątka zawiera w sobie dwie nowe czwórki i tak dalej. Tym samym odpowiedzieliśmy na pytanie bonusowe (istnieje nieskończenie wiele rozwiązań). Spróbujmy teraz znaleźć konkretny przykład.
Jako osobnik leniwy zapuściłem sobie prościutką pętelkę w Pythonie. Kod przegląda czwórki liczb pierwszych A1,A2,A3,A4 będące ciągiem arytmetycznym, a potem sprawdza czy A1+T, A2+T, A3+T, A4+T również są pierwsze, dla stosunkowo niedużego zakresu T:
from sympy import isprime, nextprime
from itertools import combinations
p = 3
pierwsze = []
zakres = 30
for i in range(zakres):
pierwsze.append(p)
p = nextprime(p)
kombinacje = combinations(pierwsze, 4)
for kombinacja in kombinacje:
for t in range(max(kombinacja) - min(kombinacja) + 2, max(kombinacja) - min(kombinacja) + zakres, 2):
if isprime(kombinacja[0]+t) and \
isprime(kombinacja[1]+t) and \
isprime(kombinacja[2]+t) and \
isprime(kombinacja[3]+t) and \
kombinacja[1]-kombinacja[0] == kombinacja[2]-kombinacja[1] and \
kombinacja[3]-kombinacja[2] == kombinacja[2]-kombinacja[1]:
print(list(kombinacja) + [n+t for n in kombinacja])
Wynik:
[5, 11, 17, 23, 41, 47, 53, 59]
[5, 17, 29, 41, 47, 59, 71, 83]
[7, 19, 31, 43, 47, 59, 71, 83]
[7, 37, 67, 97, 107, 137, 167, 197]
[11, 17, 23, 29, 41, 47, 53, 59]
[11, 41, 71, 101, 107, 137, 167, 197]
[13, 43, 73, 103, 107, 137, 167, 197]
[23, 53, 83, 113, 137, 167, 197, 227]
[37, 67, 97, 127, 137, 167, 197, 227]
[37, 67, 97, 127, 151, 181, 211, 241]
[41, 47, 53, 59, 61, 67, 73, 79]
[43, 61, 79, 97, 113, 131, 149, 167]
[53, 71, 89, 107, 113, 131, 149, 167]I faktycznie:
A jak Wam poszło?
Nadzwyczaj dobrze! Same prawidłowe odpowiedzi, a żeby było ciekawiej każda znaleziona w inny sposób.
1Pierwszy odezwał się Waldek, który wystartował identycznie jak ja, czyli sekwencją 1,2,3,4,5,6,7,8, potem zaatakował zagadnienie liczbami pierwszymi bliźniaczymi, potem dorzucił czworacze, szóstacze, ósmacze i tak dalej - do tego przykłady, obrazki i co tam panie jeszcze. Chwilami nawet do rymu. Zaliczam, z wyróżnieniem.

2Nazajutrz odezwał się Cichy Fragles, który znalazł swoje rozwiązanie metodą kartki i ołówka, "na piechotę", czyli bez wspierania się źródłami zewnętrznymi czy algorytmem komputerowym:
Oznaczmy wierzchołki, np. dolnej ściany jako a, b, c, d i górnej jako e, f, g, h (gdzie wierzchołek e łączy się z a, f z b i tak dalej). Sumy dla poszczególnych ścian wyglądają następująco: a + b + c + d = e + f + g + h = a + b + e + f = c + d + g + h = a + d + e + h = b + c + f + g. Z tej wielokrotnej równości możemy wyprowadzić kilka prostszych: a + b = g + h, b + c = h + e, c + d = e + f, a + d = f + g. Czwórek spełniających równania tego typu można łatwo znaleźć masę, biorąc dwie pary liczb pierwszych różniących się o 2 i podstawiając dwie skrajne vs dwie środkowe, np. 5 + 13 = 7 + 11. Zacząłem więc brać kolejne takie pary i metodą prób i błędów szybko znalazłem rozwiązanie: a = 11, b = 19, c = 29, d = 7, e = 31, f = 5, g = 13, h = 17.
Na pytanie bonusowe Cichy odpowiedział:
...intuicja mi podpowiada, że takich układów jest więcej.
Zaliczam - wprawdzie bez bonusa, ale za to rozwiązanie Cichego zbudowane jest z liczb dużo mniejszych niż moje czy Waldka.
3Tego samego dnia pod wieczór swoje rozwiązanie nadesłał Butter, który nie pierdzielił się w tańcu z jakimiś teoriami, tylko machnął prosty skrypt w Pythonie i "siłowo" wyszukał trzy tysiące sto siedemdziesiąt osiem kombinacji, a potem mu się znudziło. Pierwsza na liście jest kombinacja (3, 13, 17, 31, 19, 29, 5, 11) - jest to również jedyne dotychczas nadesłane rozwiązanie zawierające trójkę! Odpowiedź Buttera na pytanie bonusowe brzmi: "Jest ich w cholerę" 🙂 Zaliczam.
4Następny był Rozie, który podobnie do Buttera napisał sobie prosty skrypt w Pythonie; Rozie przyjął jednak podejście losowe (coś a'la metoda Monte Carlo) i spośród początkowych 15 liczb pierwszych losował ósemki, a potem sprawdzał czy pasują. Nawiasem mówiąc nie wiem czemu uwzględnił w zestawie sprawdzanych liczb również dwójkę - jako jedyna parzysta siłą rzeczy nie może pasować - no ale końcem końców nie wpłynęło to na wynik. Odkrył w ten sposób kombinację identyczną z butterową, a na pytanie bonusowe odrzekł, że skoro liczb pierwszych jest nieskończenie dużo, to i kombinacji dających równe sumy też. Zaliczam.
Wyjaśniam, czemu uwzględniłem dwójkę. Jest liczbą pierwszą (zresztą najmniejszą), a skoro podchodzimy do zagadnienia losowo to czemu ją wyrzucać?
BTW pominąłeś bonus bonus. Zatem: podane rozwiązanie jest najmniejsze zarówno jeśli chodzi o sumę liczb na każdym boku (64), jak i zbiór wykorzystanych początkowych liczb pierwszych: [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31]
Dwójkę pominąć należało dlatego, że jako jedyna parzysta w zestawie nie mogła być częścią rozwiązania. Ale, jak już nadmieniłem, nie wpłynęło to zupełnie na wynik końcowy więc nie dzielmy włosa na czworo 😉