Tradycyjne Sudoku o rozmiarach 9x9 pól to jedna z najpopularniejszych łamigłówek kibelkowych[citation needed]. Dziś odrobina statystyk, bo mi się chwilowo skończyły inne tematy.
- 6 670 903 752 021 072 936 960 (sześć tryliardów z hakiem, 6.67 x 1021) to całkowita liczba wszystkich możliwych rozwiązań Sudoku (czyli plansz wypełnionych 81 cyferkami).
- Ponieważ jednak w Sudoku można znaleźć aż 26 różnego rodzaju symetrii, faktyczna liczba łamigłówek, które znacząco różnią się od siebie, wynosi zaledwie - uwaga - 5 472 730 538 (5.47 x 109). Wszystkie pozostałe kombinacje można uzyskać z jednej z tych pięciu miliardów przekształconej przez symetrię (obrót, odbicie, zamianę cyfr, zamianę wierszy lub jakąś inną).
- Najmniejsza łamigłówka minimalna (tj. taka pozycja startowa, od której nie da się już zabrać żadnej cyfry bez utraty jednoznaczności rozwiązania) musi mieć co najmniej 17 cyfr.
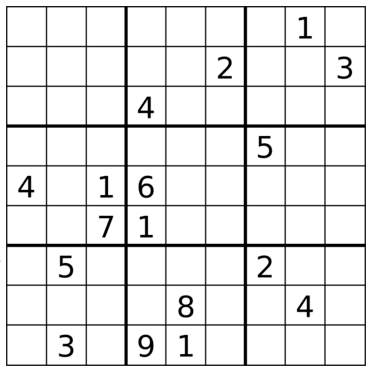

- Nie udało się ustalić, czy istnieje łamigłówka 17-cyfrowa z podwójną symetrią (tj. względem obydwu przekątnych); najmniejsza taka łamigłówka, jaką udało się dotychczas znaleźć, ma 18 cyfr:
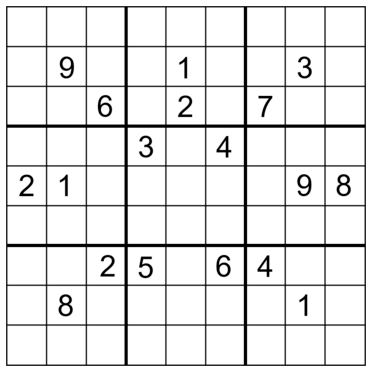
- Dla każdego rozwiązania da się znaleźć łamigłówkę minimalną z nie więcej niż 24 cyframi.
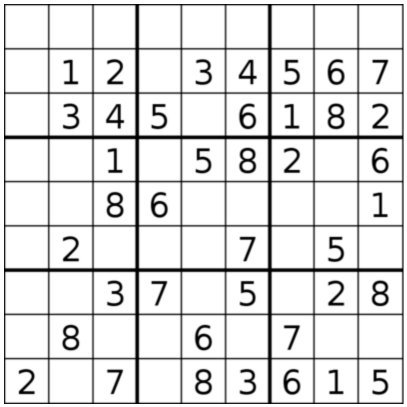
- Nie wiadomo ile wynosi największa możliwa liczba cyfr łamigłówki minimalnej. Jak na razie udało się znaleźć tylko dwie łamigłówki minimalne 40-cyfrowe. Nie wiadomo czy istnieją większe.
- Nie wiadomo dokładnie ile jest wszystkich łamigłówek minimalnych Najlepsze znane obecnie przybliżenie (z dokładnością do około pół promila) to:
- około 3.1 x 1037 wszystkich łamigłówek minimalnych
- około 2.55 x 1025 łamigłówek minimalnych po eliminacji symetrii
- Największy pusty prostokątny obszar na planszy 9x9, dla którego da się ułożyć rozwiązywalną łamigłówkę ma 30 pól (prostokąt 5x6):

- Najmniejsza plansza Sudoku, dla której liczba wszystkich możliwych rozwiązań przekracza liczbę atomów we Wszechświecie to plansza 15x15 pól (podzielona na 15 prostokątów 3x5), dla której istnieje około 3.5 x 1084 poprawnych rozwiązań.
Dzisiejszy wpis jest skompresowanym wyciągiem z tego artykułu. Polecam lekturę - jest tam mnóstwo interesujących klamotów o metodach liczenia tych wszystkich wielkich liczb, o innych wariantach gry oraz sporo ciekawych odnośników do innych stron o Sudoku jakby komuś było za mało 😉
Ale i tak liczba możliwych rozwiązań jest niższa niż ilość odcinków Mody na Sukces.
Dodatkowo – takie duże liczby lepiej podawać w sasinach: 95 298 625 028 872.46875
Ha! Nie cierpię sudoku – jest nudne. Konkretny, ale długi, nużący i skomplikowany algorytm prowadzi zawsze do rozwiąznia. Świadomość, że mechaniczne powtarzanie pewnych kroków da w końcu rezultat psuje mi zabawę. Dla mnie kicha…
Co innego sudoku z czarnymi i białymi kropkami. Te lubię, zwłaszcza takie bardziej dopracowane. Pusta plansza – bez żadnych cyfr – kombinuj. Jeśli zadanie jest z tych bardziej ambitnych, to reguły są dobrze ukryte i wtedy nawet kilka godzin można nad nim się pomęczyć.
Coś więcej o tej wersji z kropkami?
https://external-content.duckduckgo.com/iu/?u=http%3A%2F%2Fimgcdn.geocaching.com%2Fcache%2Flarge%2F48be5484-8ba6-4756-a444-1a3f4afd01b9.jpg&f=1&nofb=1
Biała kropka oznacza, że cyfry na sąsiednich polach różnią się o 1.
Czarna kropka oznacza, że jedna z cyfr jest dwa razy większa od drugiej.
Wszystkie możliwe kropki są zaznaczone.
W przypadku sąsiadujących cyfr 1 i 2 jest albo biała, albo czarna kropka – nie wiadomo.
Powyższa plansza jest łatwym zadaniem. Niemal z marszu można wypełnić wiele pól. W ambitniejszych zadaniach jest 10-13 czarnych kropek i z reguły to ich liczba i układ decydują o stopniu trudności, choć jest wiele wyjątków.