Dziś pokażę interesującą (przynajmniej dla mnie...) technikę eliminowania kandydatów w Sudoku.
Żeby było jasne: nie prowadzę żadnej agencji rekrutacyjnej, w której eliminuję kandydatów. Chodzi wyłącznie o kandydatów w sensie cyfr pasujących w danym momencie do danego kwadratu. A Emil... to był wypadek i tej wersji będę się trzymał dopóki nie kupię znajdę wiarygodnego świadka.
Technologia ta nazywa się po angielsku X-Chains. X od eXclude czyli wyłączyć, wyeliminować, wykluczyć, a Chains to łańcuchy. Ponadto, X wygląda jak krzyżyk, a celem X-Chains jest wyeliminowanie kandydata na skrzyżowaniu dwóch innych komórek.
Zasadnicza idea łańcuchów polega na tym, że...
To ja może od razu na przykładzie.
Spójrzmy na poniższy kwadrat:
Przyjrzyjmy się uważniej komórce r6c1 (r6c1 oznacza szósty wiersz, pierwsza kolumna czyli komórka w lewej kolumnie, zaraz pod dwójką). Możliwe cyfry to 5, 8 lub 9.
Kolejna komórka: r9c1 (dolny lewy róg). Tutaj możliwe cyfry to 5 lub 9.
I kolejna: r9c8 (oczko w lewo od dolnego prawego rogu): tutaj jedyne możliwości do 1 lub 9.
Następna: r8c7: również tylko 1 lub 9.
Wreszcie r6c7, z kandydatami 2, 5, 7, 9.
Komórki r6c1, r9c1, r9c8 oraz r8c7 tworzą łańcuch, dzięki któremu będziemy mogli wyeliminować dziewiątkę z komórki r6c7.
W jaki sposób?
Popatrzmy: jeżeli w r6c1 byłaby dziewiątka, to w r9c1 nie może być dziewiątki, wówczas w r9c8 musi być dziewiątka, czyli w r8c7 dziewiątki nie ma.
A teraz na odwrót: jeżeli w r6c1 nie ma dziewiątki, wówczas musi ona być w r9c1 (w całej lewej kolumnie nie ma innych komórek dla dziewiątki), a więc nie ma jej w r9c8, czyli musi być w r8c7 (bo w dolnym prawym kwadracie 3x3 są tylko dwie komórki z możliwą dziewiątką: r9c8 i r8c7).
W obydwu powyższych wariantach, dziewiątka znajduje się albo w r6c1 albo w r8c7. Tym samym w komórce r6c7 (która "widzi" zarówno r6c1 jak i r8c7) nie może być dziewiątki, więc eliminujemy ją stamtąd.
Poniżej wyjaśnienie "obrazkowe". Dziewiątka w komórce r6c7 może być bezpiecznie wyeliminowana.
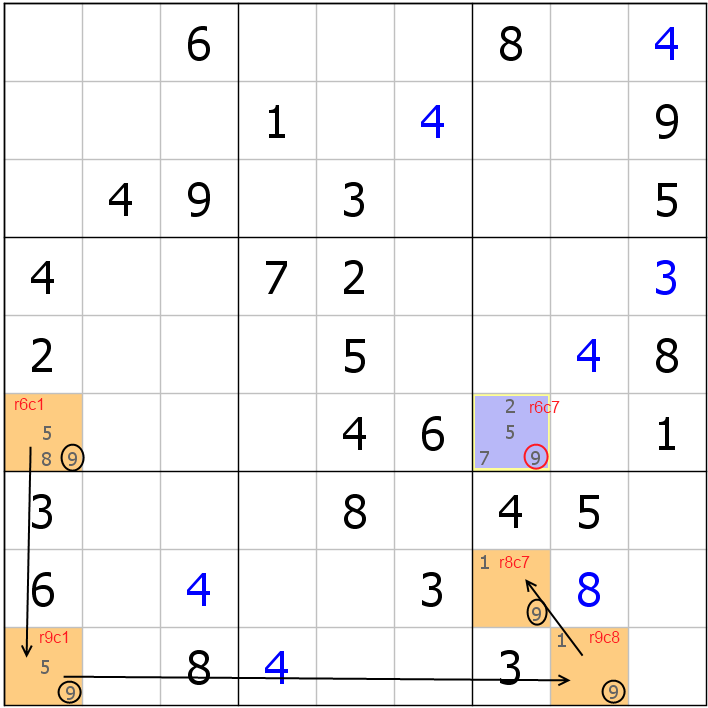
http://odkrywcy.pl/kat,111408,title,Te-lamiglowke…
Rozwiązywanie tego typu łamigłówek jest równie porywające jak granie w szachy z Deep Blue. Znaczy się, nie dla ludzi.
Jak czas pozwoli, wrzucę dziś to sudoku do analizatora, zobaczymy co on na to.
Bledne zalozenie , ze musi byc 9tka w r9c8, rownie dobrze moze byc w r8c7 – w etaie po drugiej strzlce
Metoda łańcuchów krzyżowych polega na znalezieniu dwóch możliwych alternatyw, z których każda wyklucza daną cyfrę w pewnej konkretnej komórce. W tym przypadku obydwie alternatywy (a więc zarówno ta, gdzie dziewiątka w R6C1 jest jak też ta, gdzie jej tam nie ma) wykluczają dziewiątkę w R6C7. Nie wiemy zatem, czy w R6C1 jest dziewiątka czy nie, ale wiemy na pewno, że dziewiątki nie ma w R6C7.