Zagadkę da się sposób rozpykać za pomocą brute-force:
def ZnajdźProstopadłościan(przekątna):
NajwiększaObjętość = 0
Wymiary = (0, 0, 0) # (a, b, c)
for a in range(1, przekątna):
for b in range(a, przekątna): # Zaczynamy od a żeby uniknąć zduplikowanych par
for c in range(b, przekątna): # Zaczynamy od b z tego samego powodu
if a**2 + b**2 + c**2 == przekątna**2:
Objętość = a * b * c
if Objętość > NajwiększaObjętość:
NajwiększaObjętość = Objętość
Wymiary = (a, b, c)
return Wymiary, NajwiększaObjętość
przekątna = 2024
Wymiary, Objętość = ZnajdźProstopadłościan(przekątna)
print(Wymiary, Objętość)
Powyższy kod wykonuje się na moim wysłużonym i7 dobrze ponad 6 minut - i nie dziwota, bo nawet po eliminacji duplikatów nadal mamy coś z miliard wykonań pętli wewnętrznej, z sześcioma mnożeniami, dwoma dodawaniami i Wogle. Ale po zakończeniu wypluwa on:
(1104, 1104, 1288) 1569835008
Mamy więc odpowiedź do pierwszego pytania.
Zauważamy przy okazji, że nasz prostopadłościan jest prawie sześcianem. Sześcian z taką przekątną miałby długość boku około 1168.56 i objętość około 1595706627 - a więc nasze rozwiązanie jest "odległe" od sześcianu zaledwie o 1.6%.
Drugie pytanie było przewrotne ponieważ dotyczyło dokładnie tego samego problemu, tylko w drugą stronę: szukamy prostopadłościanu o przekątnej 2024 i krawędziach całkowitych dodatnich, ale z najmniejszą możliwą objętością. Zamieniając znak większości na mniejszości w powyższym kodzie (oraz startując z objętością od p3 zamiast od zera) dostaniemy następujący wynik:
(64, 168, 2016) 21676032I to jest poprawna odpowiedź na pytanie bonusowe. Natomiast jeżeli chodzi o zadanie bonusowe na sterydach, czyli szukanie najpojemniejszego prostopadłościanu "na piechotę" to temat robi się zdecydowanie ciekawszy.
Zaczniemy od prostej matematyki. Z Pitagorasa mamy: $$a^2+b^2+c^2=p^2$$ Skoro p=2024, to szukamy trójki liczb (a, b, c) takich, że suma ich kwadratów wynosi 4096576. Pamiętajmy jednak, że mamy do dyspozycji wyłącznie kartkę i ołówek. Szukanie takiej trójki może nam więc trochę zająć...
Ale, ale. Przekątna ma wymiar liniowy, podobnie jak krawędź. A więc skrócenie przekątnej o połowę powinno nam też zmniejszyć długość każdej krawędzi o połowę. Prawda?
Sprawdźmy: $$\left(\frac{a}{2}\right)^2+\left(\frac{b}{2}\right)^2+\left(\frac{c}{2}\right)^2=\left(\frac{p}{2}\right)^2$$ Mnożąc obie strony przez 4 dostajemy to samo co na początku, czyli wszystko się zgadza. Zamiast dwójki możemy oczywiście użyć (prawie) dowolnej innej liczby.
No dobra. To już coś.
2024 dzieli się przez 8, 11 i 23 (co łatwo sprawdzić na piechotę). A więc jeżeli przeskalujemy przekątną w dół do 11 (czyli podzielimy początkowe 2024 przez 8 i potem jeszcze przez 23) i znajdziemy rozwiązanie dla takiego małego prostopadłościanu, to potem wystarczy przeskalować wynik w drugą stronę et voila!
112=121[citation needed]
Szukamy więc trzech liczb a, b, c takich, że: $$a^2+b^2+c^2=121$$, pamiętając jednocześnie, że: $$0 < a <= b <= c < 11$$
Kombinacji jest w dalszym ciągu parę setek, ale po pierwsze parę setek to nie miliardy, a po drugie zanim zaczniemy jak jakaś porąbana mróweczka sprawdzać kolejne kombinacje, zauważamy jeszcze coś. Otóż wiadomo, że optymalne rozwiązanie - o ile istnieje - będzie kształtem w miarę możliwości zbliżone do sześcianu. Jedna trzecia ze 121 to pi x drzwi 40, a więc warto zacząć od kwadratów, których wartości lądują w pobliżu 40. 62=36 (blisko), 72=49 (też blisko), więc sprawdzamy na dzień dobry szóstki i siódemki. I faktycznie: $$6^2+6^2+7^2=36+36+49=121$$ W końcu skalujemy ten wynik w górę: 6*8*23=1104, 7*8*23=1288 - noż kurdę, zgadza się!
PostScriptum: powyższa metoda działa tylko dla niektórych przekątnych, o czym poinformował mnie Waldek (patrz komentarze). Nie ma róży bez kolców, czy coś...
Zanim jednak założymy na głowę zwycięski laur zwycięstwa... znaczy, tego, laur... no dobra, zanim więc zaczniemy pląsać z radości w blasku księżyca, odpowiedzmy sobie jeszcze na jedno, ale to za*ście ważne pytanie.

A mianowicie: dlaczego zredukowaliśmy przekątną z 2024 akurat do 11, a nie, dajmy na to, do 2? Przecież skoro 2024 dzieli się przez 1012, to zamiast kombinować z 112 moglibyśmy równie dobrze kombinować z 22, prawda? Mniejsza liczba, mniej kombinowania. No więc jak to jest?
A no jest tak, że 4 jest po prostu za małe, żeby je przedstawić w postaci sumy trzech kwadratów. Nie da się i już.
Jeżeli szukalibyśmy rozwiązania uniwersalnego (tj. dla każdej możliwej przekątnej a nie tylko 2024), to po rozkładzie długości przekątnej na czynniki pierwsze musimy wybrać najmniejszy z nich, ale różny od 2 lub 5 - a następnie znaleźć dlań sumę trzech kwadratów (może być siłowo).
A czemu różny od 5?
Tu w sukurs przychodzi nam twierdzenie Legendre'a o sumie trzech kwadratów, które mówi, że liczba naturalna może być przedstawiona w postaci sumy kwadratów trzech liczb naturalnych wtedy i tylko wtedy, jeżeli nie jest ona postaci 4k(8m+7). Dla przekątnej p=5 mamy 52=25=40(8*2+7), czyli dupa. Natomiast wszystkie liczby pierwsze większe od 5 podniesione do kwadratu nie dają się przedstawić w postaci 8m+7 (dowód pozostawiam Czytelnikowi - trzeba wystartować od faktu, że dowolna liczba pierwsza większa od 3 jest postaci 6k±1), więc dla wszystkich pozostałych liczb pierwszych p da się znaleźć co najmniej jedną trójkę (a, b, c) taką, że suma ich kwadratów daje p2, co zresztą sprawdziłem eksperymentalnie Pythonem aż do p=10000 - zgadza się.
from sympy import primerange
def find_positive_squares_for_prime(prime):
target = prime ** 2
for x in range(1, prime + 1):
for y in range(x, prime + 1):
for z in range(y, prime + 1):
if x ** 2 + y ** 2 + z ** 2 == target:
return (x, y, z)
return None
for p in primerange(2, 10000):
print(p, find_positive_squares_for_prime(p))
Ostrzegam lojalnie: duuuuużo czekania, bo czym większe p, tym dłużej się liczy.
A jak Wam poszło?
1Jako pierwszy odezwał się tacitgreg, którego odpowiedź na pytanie główne jest poprawna, bonusowe - niepoprawna, a zadanie "na piechotę" w ogóle nie ruszone. Nie zaliczam (acz strona www imponująca!)

2Drugim rozwiązującym był Greg. Bez adresu, więc nie wiem czy to ten sam Greg co przedtem, czy jakiś inny. Odpowiedzi na dwa pierwsze pytania poprawne, ostatnie nie ruszone. Od biedy mogę zaliczyć na żółto/pomarańczowo.

3Również na żółto/pomarańczowo zaliczam Roziemu, który odezwał się jako trzeci.

4Podobnie sytuacja wygląda ze zgłoszeniem Buttera, które nadeszło w chwilę później. Dwie poprawne odpowiedzi, trzeciej brak. Żółtopomarańczowo.

5W ostatniej chwili zgłosił się Waldek - i pozamiatał.
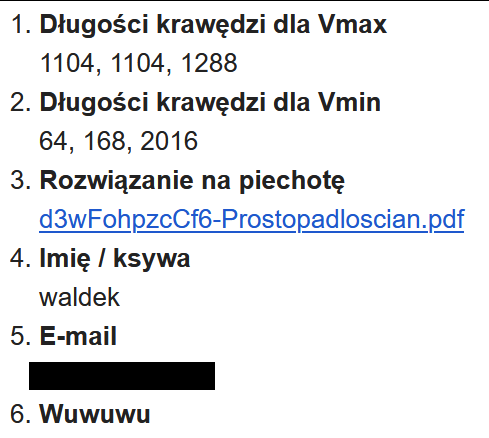
Żeby nie było nudno, swoje rozwiązanie na piechotę Waldek okrasił własną zagadką:

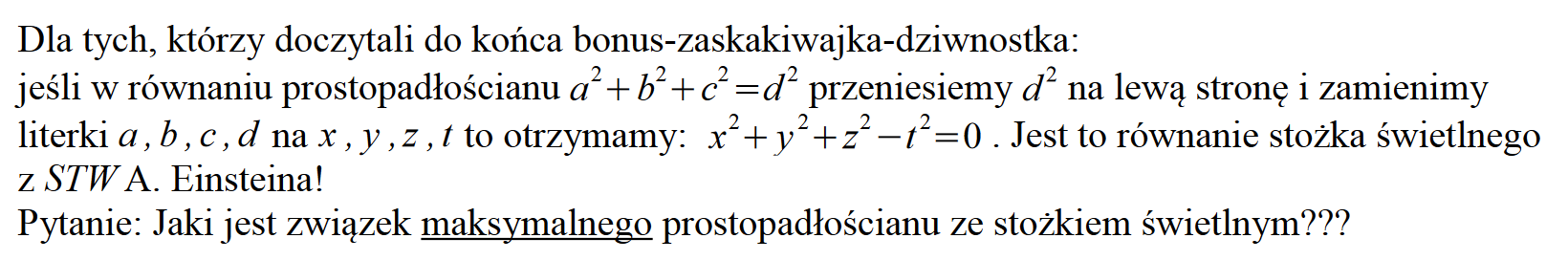
Mam kilka komentarzy o większym, mniejszym i żadnym znaczeniu:
U1.
Nasze rozwiązania są bardzo podobne, więc nadal pozostaje problem, czy po powrotnym przeskalowaniu wyniku do pierwotnego rozmiaru istnieje większy prostopadłościan. Dla 2024 akurat takiego nie ma, ale dla 2030 można już taki wskazać:
Jeżeli podzielimy 2030/10=203 to uzyskamy:
d=203 a=90 b=122 c=135 ==> v=1482300
Po powrotnym pomnożeniu wyników przez 10:
d=2030 a=900 b=1220 c=1350 ==> v=1.482.300.000
Tymczasem istnieje znacznie większy prostopadłościan. Nie został on znaleziony powyższą metodą, gdyż przynajmniej jedna z długości nie jest podzielna przez czynnik skalujący, czyli przez 10:
d=2030 a=1140 b=1146 c=1228 ==> v=1.604.308.320
U2.
„Dla przekątnej p=5 mamy 5^2=25=4^0(8*2+7), czyli dupa”
4^0(8*2+7)=23 czyli dwie dupy. 🙂
U3.
Mój CPU: i5 3,4 GHz i program w Delphi w zasadzie identyczny z twoim, po dopisaniu instrukcji liczenia czasu, wypluł mi to:
d=2024
a=1104 b=1104 c=1288 v=1569835008
a=64 b=168 c=2016 v=21676032
czas obliczeń: 624 ms
W C++ jeszcze kilkanaście milisekund szybciej.
U1: Faktycznie! Wprowadziłem stosowną notkę we wpisie.
U2: Nie łapię, 23 nie jest kwadratem liczby naturalnej…
U3: Niektórzy czytelnicy raportują mi, że ten sam kod uruchomiony za pomocą PyPy działa w około minutę. Możesz się we wolnej chwili pochwalić swoim kodem w Delphi / C++? Bardzo-m ciekaw.
U2: Napisałeś: „Dla przekątnej p=5 mamy 5^2=25=4^0(8*2+7)”.
Tymczasem 4^0(8*2+7)=23. Krótko mówiąc wykazałeś, że 25=23.
U3: Kod jak kod, w zasadzie identyczny z twoim, tu nie da się wymyślić koła. Mam tylko jedną drobną różnicę – pętlę While zamiast For – jak powszechnie wiadomo czasem działa szybciej, choć akurat nie tu. Sprawdziłem dla For – wyszło 644 ms.
Mam też jedną dodatkową instrukcję Break, której w twoim kodzie brak. Przerywa ona pętlę, gdy obliczona przekątna jest większa od d^2. Bez tego Break’a czas wykonania zwiększa się do 933 ms, czyli nadal siedem razy szybciej niż u Ciebie..
procedure Prostopadloscian(d: integer); var x, y, z, d2, d2akt, xmax, ymax, zmax, v, vmax: integer; begin vmax:=0; d2:=d*d; x:=1; While x<=d-2 do begin y:=x; While y<=d-1 do begin z:=y; While z<=d do begin d2akt:=x*x+y*y+z*z; if d2akt>d2 then Break else if d2akt=d2 then begin v:=x*y*z; if v>vmax then begin vmax:=v; xmax:=x; ymax:=y; zmax:=z; end; end; Inc(z); end; Inc(y); end; Inc(x); end; Form1.Memo1.Lines.Add('d='+IntToStr(d)); Form1.Memo1.Lines.Add('x='+IntToStr(xmax)+' y='+IntToStr(ymax)+ ' z='+IntToStr(zmax)+' v='+IntToStr(vmax)); end;Jest darmowa wersja Pascala o nazwie Lazarus. Mało waży, instaluje się 9 sekund, działa identycznie, jak Delphi i dopóki nie korzystasz z zaawansowanych bibliotek, to kod jest niemal identyczny z tym w Pythonie – nie trzeba się uczyć. Możesz ściągnąć i sam sprawdzić jakie wyniki uzyskasz na swoim kompie.
Jestem ciekaw, gdyż od czasu do czasu pokazujesz swoje kody i cierpisz z powodu długich obliczeń. Pamiętam, że co najmniej dwa, a może trzy razy robiłeś coś w pętli ograniczonej do tysięcy cykli, podczas, gdy u mnie to samo liczyłem do 10^8 cykli w podobnym lub krótszym czasie. Była pewna różnica – ty w Pythone wywoływałeś jakąś biblioteczną funkcję i kończyłeś program w kilku linijkach, a ja tę funkcję musiałem pisać od zera. Ale każdy robi to, co lubi, ogusty nie dyskutują.
Nie chciało mi się instalować tego Paszczala, ale wykombinowałem prostą optymalizację w Pythonie: zamiast sprawdzać d^2 dla wszystkich kombinacji (a, b, c), skoro znamy d, wystarczy sprawdzić wszystkie kombinacje (a, b), dla których d^2-a^2-b^2 jest całkowite:
import time def GereszKantorGeresz(przekątna): objętość_max = 0 wymiary_max = (0, 0, 0) for a in range(1, przekątna): for b in range(a, przekątna): c_kwadrat = przekątna**2 - a**2 - b**2 if c_kwadrat >= 0: c = c_kwadrat**0.5 if c.is_integer(): objętość = a * b * int(c) if objętość > objętość_max: objętość_max = objętość wymiary_max = (a, b, int(c)) return wymiary_max, objętość_max przekątna = 2024 t1=time.time() print(GereszKantorGeresz(przekątna)) t2=time.time() print(t2-t1)(nazwę procedury przekornie wymyśliłem ze starego serialu węgierskiego o psie policyjnym o imieniu Kantor. O ile pamiętam, „Szukaj, Kantor, szukaj” brzmiało właśnie „Geresz, Kantor, geresz”, a może mi się całkiem pomyliło…)
Kod wykonuje się w „zwykłym” Pythonie poniżej sekundy, w PyPy pewnie dużo krócej (nie sprawdzałem, leniwy jestem)
… dodatkowo, jeżeli dodamy `break` tu i ówdzie (po co sprawdzać wszystkie kombinacje (a, b) skoro i tak już wyskoczyliśmy poza limit?), a następnie zatrudnimy PyPy, czas wykonania spada do około 140 milisekund:
import time def GereszKantorGeresz(przekątna): objętość_max = 0 wymiary_max = (0, 0, 0) for a in range(1, przekątna): for b in range(a, przekątna): c_kwadrat = przekątna**2 - a**2 - b**2 if c_kwadrat < 0: break else: c = c_kwadrat**0.5 if c.is_integer(): objętość = a * b * int(c) if objętość > objętość_max: objętość_max = objętość wymiary_max = (a, b, int(c)) return wymiary_max, objętość_max przekątna = 2024 t1=time.time() print(GereszKantorGeresz(przekątna)) t2=time.time() print(t2-t1)Znalazłem chwilę by się pobawić w optymalizację. Również miałem wersję z iterowaniem po 3 zmiennych, w dodatku w zakresie 1-2023 każda. Wrzuciłem do ChatGPT z prośbą o optymalizację i zaproponował dokładnie to, czego użyłeś, czyli pozbycie się iterowania po trzeciej zmiennej. Trochę błędów zrobił (int z zespolonej…), ale zasadnicza część optymalizacji poprawna.
Przychodzi mi jeszcze do głowy użycie
for a in range(1, 1+przekątna//2)
Powinno zredukować obliczenia o połowę, choć na czas już zauważalnie nie wpłynie.