Przelewana zagadka: rozwiązanie

https://xpil.eu/nrn

Niezależnie od tego czy w obydwu naczyniach będzie na początku tyle samo wody czy nie, szybko zorientujemy się, że w A pozostanie zawsze mniej więcej dwa razy więcej wody niż w B. Czym dłużej będziemy przelewać, tym bliżej proporcji 2:1 się znajdziemy.

a, b = 10, 10
for i in range(100):
        b = b + a / 2
        a = a / 2
        a = a + b / 2
        b = b / 2
print(a, b, a / b)

Wynik:

13.333333333333332 6.666666666666666 2.0

Jeżeli wystartujemy od a=1 i b=10000, dostaniemy:

6667.333333333332 3333.666666666666 2.0

Czyli zawsze w pierwszym kubełku będzie mniej więcej dwa razy więcej wody niż w drugim.

A jak to udowodnić algebraicznie?

Najpierw wymyślamy sobie taką jednostkę miary, żeby łączna ilość wody wyniosła 1. Następnie ustalamy, że w jednym kubku jest 2/3+x, tym samym w drugim: 1/3-x.

Na start mamy więc: \((A, B) = (\frac{2}{3}+x, \frac{1}{3}-x)\).

Przelewamy z A do B i zaraz potem z B do A: \( (\frac{1}{3}+\frac{x}{2}, \frac{2}{3}−\frac{x}{2}), (\frac{2}{3}+\frac{x}{4}, \frac{1}{3}−\frac{x}{4}) \)

Innymi słowy jeden krok zamienił nam \((\frac{2}{3}+x, \frac{1}{3}-x)\) na \((\frac{2}{3}+\frac{x}{4}, \frac{1}{3}−\frac{x}{4}) \).

Kolejny krok da nam więc \((\frac{2}{3}+\frac{x}{16}, \frac{1}{3}−\frac{x}{16})\), następny \((\frac{2}{3}+\frac{x}{64}, \frac{1}{3}−\frac{x}{64})\) i tak dalej - widzimy, że 2/3 i 1/3 pozostają bez zmian, a liczba, którą od nich odejmujemy maleje bardzo szybko (z kolejnymi potęgami czwórki).

\[ \lim_{n\to\infty} \frac{1}{4^n}=0 \]

W granicy pozostaje nam więc: \((\frac{2}{3}, \frac{1}{3})\), czyli poprawna odpowiedź to 2.

A jak Wam poszło?

W odróżnieniu od poprzedniej zagadki, do której nie podszedł nikt, tutaj odzew był całkiem całkiem.

1Na pierwszy ogień poszedł Rozie, który napisał prościutki symulator w Pythonie, całkiem podobny do tego powyżej, tylko trochę inny:

a = 10
b = 10
for i in range(0,10):
	c = a / 2
	a -= c
	b += c
	c = b / 2
	a += c
	b -= c
print(a, b)

Rozie udzielił poprawnej odpowiedzi, więc zgodnie z odwieczną zasadą "kto pierwszy ten lepszy" dostaje on WMZZ (Wielki Medal Z Ziemniaka) - gratulacje! Niestety ze względu na pandemię medal proszę sobie wykonać samodzielnie i we własnym zakresie 🙂

2Chronologicznie drugim zgadującym był Butter, który również udzielił poprawnej odpowiedzi, ale bez szczegółów sposobu jej uzyskania. Napisał tylko:

"Po kilku cyklach proporcja A do B stabilizuje się na poziomie 2:1 [1:2 w co drugim cyklu]."

-- Butter, A.D. 2021

3Trzeci odezwał się Cichy Fragles - również poprawna odpowiedź oraz następujące objaśnienie:

Oznaczmy ilość wody w naczyniach jako a i b. Po pierwszym przelaniu ilości te wynoszą a/2 oraz b + a/2. Po przelaniu w drugą stronę dostajemy odpowiednio 3a/4 + b/2 oraz b/2 + a/4, co możemy ładniej zapisać jako (a/2 + b/2) + a/4 oraz (a/2 + b/2) - a/4. Czyli różnica między naczyniami po jednym cyklu wyniesie zawsze a/2, z czego wniosek, że jeśli a > 2b, to wody w pierwszym naczyniu ubędzie, a w przeciwnym razie jej przybędzie. Proporcja musi więc asymptotycznie dążyć do 2:1, niezależnie od początkowych wartości.

-- C.F.

4Czwartym (i ostatnim) czytelnikiem, który podszedł do zagadki, był Waldek, który - udzieliwszy poprawnej odpowiedzi - objaśnił zagadnienie cięższą artylerią. Są limesy, są ułamkowe indeksy, jest nawet delta (to dla tych, którzy się zastanawiali czy liczenie delty trójmianu kwadratowego im się kiedykolwiek do czegokolwiek przyda):

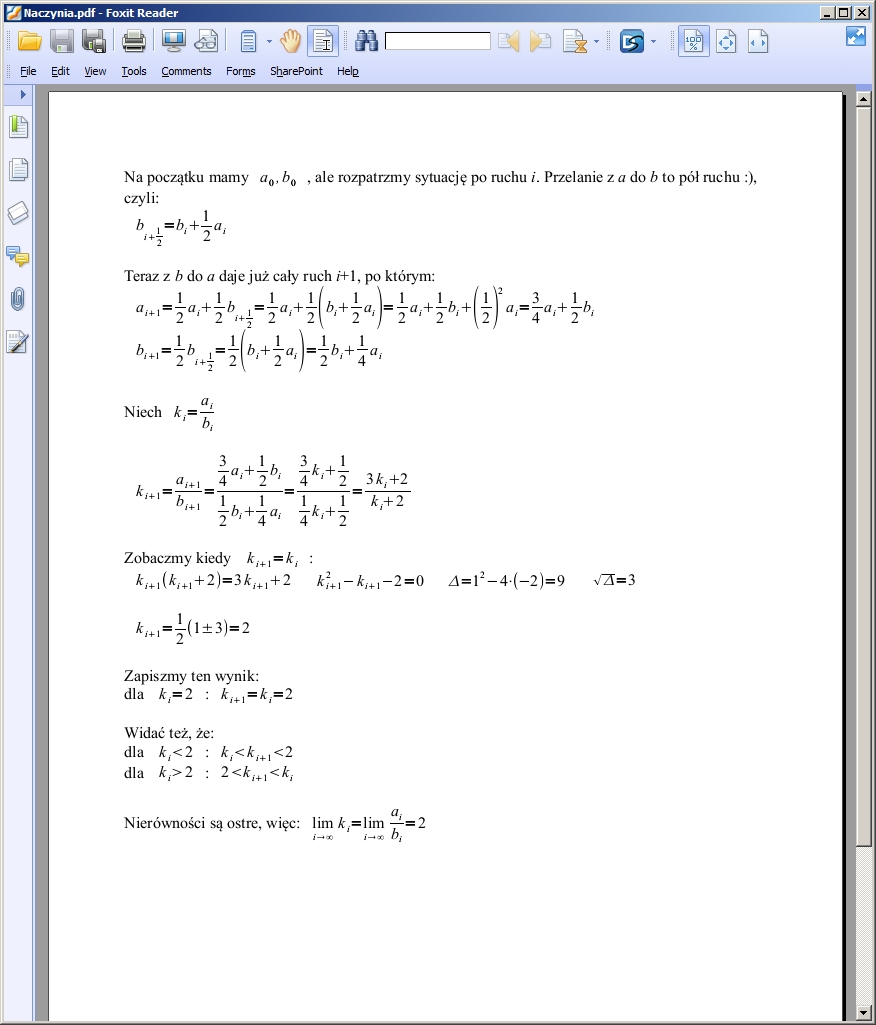
Za wybitne zasługi Waldka w szerzeniu matematycznej rozpusty udzielam mu niniejszym srogiej pochwały. Well done!

https://xpil.eu/nrn