W zagadce chodziło o ustalenie po jakim czasie trzy planety A, B i C znów ustawią się w jednej linii zakładając, że startujemy od ustawienia współliniowego po tej samej stronie słońca, oraz że wszystkie trzy krążą w tej samej płaszczyźnie i okrążają słońce w czasie odpowiednio 3, 4 i 5 lat a także są odległe od słońca o 3, 4 i 5 jednostek.
Na początku zauważymy, że warunkiem wystarczającym do tego, żeby trzy punkty były współliniowe jest to, że zbudowany na ich bazie trójkąt będzie zdegenerowany (tj. o powierzchni zero). Pole trójkąta o znanych długościach boków policzyć łatwo (ze wzoru Herona), długości boków można policzyć ze współrzędnych wierzchołków (z Pitagorasa), a współrzędne wierzchołków w czasie też łatwo policzyć z sinusa i kosinusa, znając prędkości kątowe.
Spróbujmy więc napisać sobie funkcję, która wylicza pole tego trójkąta w zależności od czasu t.
Zaczniemy od prędkości kątowych: A okrąża słońce w 3 lata, więc krąży z prędkością kątową 2π/3, B: 2π/4, C: 2π/5.
A więc kąt odchylenia od początkowego ustawienia (które przyjmiemy dla ułatwienia za równe 0) w chwili t wynosi odpowiednio 2tπ/3,2tπ/4 oraz 2tπ/5.
Znając te kąty możemy sobie teraz policzyć współrzędne wierzchołków w każdej chwili t:
Ogólnie x = cos(kąt), y = sin(kąt), u nas będzie sześć współrzędnych:
xa=cos(2tπ/3), ya=sin(2tπ/3), xb=cos(2tπ/4), yb=sin(2tπ/4), xc=cos(2tπ/5), yc=sin(2tπ/5)
Długości boków trójkąta liczymy z Pitagorasa, czyli:
\(D_{ab}=\sqrt{(x_a-x_b)^2 +(y_a-y_b)^2}\) \(D_{bc}=\sqrt{(x_b-x_c)^2 +(y_b-y_cb)^2}\) \(D_{ac}=\sqrt{(x_a-x_c)^2 +(y_a-y_c)^2}\)Połowę obwodu policzyć łatwo:
\(S=\frac{\sqrt{(x_a-x_b)^2 +(y_a-y_b)^2}+\sqrt{(x_b-x_c)^2 +(y_b-y_cb)^2}+\sqrt{(x_a-x_c)^2 +(y_a-y_c)^2}}{2}\)Wzór Herona mówi, że pole trójkąta to:
\(P = \sqrt{S(S-D_{ab})(S-D_{bc})(S-D_{ac})}\)Podstawiając dostajemy:
\(P = \sqrt{\frac{\sqrt{(x_a-x_b)^2 +(y_a-y_b)^2}+\sqrt{(x_b-x_c)^2 +(y_b-y_cb)^2}+\sqrt{(x_a-x_c)^2 +(y_a-y_c)^2}}{2}(\frac{\sqrt{(x_a-x_b)^2 +(y_a-y_b)^2}+\sqrt{(x_b-x_c)^2 +(y_b-y_c)^2}+\sqrt{(x_a-x_c)^2 +(y_a-y_c)^2}}{2}-\sqrt{(x_a-x_b)^2 +(y_a-y_b)^2})(\frac{\sqrt{(x_a-x_b)^2 +(y_a-y_b)^2}+\sqrt{(x_b-x_c)^2 +(y_b-y_c)^2}+\sqrt{(x_a-x_c)^2 +(y_a-y_c)^2}}{2}-\sqrt{(x_b-x_c)^2 +(y_b-y_c)^2})(\frac{\sqrt{(x_a-x_b)^2 +(y_a-y_b)^2}+\sqrt{(x_b-x_c)^2 +(y_b-y_c)^2}+\sqrt{(x_a-x_c)^2 +(y_a-y_c)^2}}{2}-\sqrt{(x_a-x_c)^2 +(y_a-y_c)^2})} \)Wreszcie podstawiając za iksy i igreki dostajemy pole w funkcji czasu:
\(P = \sqrt{\frac{\sqrt{(cos(2tπ/3)-cos(2tπ/4))^2 +(sin(2tπ/3)-sin(2tπ/4))^2}+\sqrt{(cos(2tπ/4)-cos(2tπ/5))^2 +(sin(2tπ/4)-sin(2tπ/5))^2}+\sqrt{(cos(2tπ/3)-cos(2tπ/5))^2 +(sin(2tπ/3)-sin(2tπ/5))^2}}{2}(\frac{\sqrt{(cos(2tπ/3)-cos(2tπ/4))^2 +(sin(2tπ/3)-sin(2tπ/4))^2}+\sqrt{(cos(2tπ/4)-cos(2tπ/5))^2 +(sin(2tπ/4)-sin(2tπ/5))^2}+\sqrt{(cos(2tπ/3)-cos(2tπ/5))^2 +(sin(2tπ/3)-sin(2tπ/5))^2}}{2}-\sqrt{(cos(2tπ/3)-cos(2tπ/4))^2 +(sin(2tπ/3)-sin(2tπ/4))^2})(\frac{\sqrt{(cos(2tπ/3)-cos(2tπ/4))^2 +(sin(2tπ/3)-sin(2tπ/4))^2}+\sqrt{(cos(2tπ/4)-cos(2tπ/5))^2 +(sin(2tπ/4)-sin(2tπ/5))^2}+\sqrt{(cos(2tπ/3)-cos(2tπ/5))^2 +(sin(2tπ/3)-sin(2tπ/5))^2}}{2}-\sqrt{(cos(2tπ/4)-cos(2tπ/5))^2 +(sin(2tπ/4)-sin(2tπ/5))^2})(\frac{\sqrt{(cos(2tπ/3)-cos(2tπ/4))^2 +(sin(2tπ/3)-sin(2tπ/4))^2}+\sqrt{(cos(2tπ/4)-cos(2tπ/5))^2 +(sin(2tπ/4)-sin(2tπ/5))^2}+\sqrt{(cos(2tπ/3)-cos(2tπ/5))^2 +(sin(2tπ/3)-sin(2tπ/5))^2}}{2}-\sqrt{(cos(2tπ/3)-cos(2tπ/5))^2 +(sin(2tπ/3)-sin(2tπ/5))^2})}\)Proste?
No pewnie, teraz wystarczy to tylko wrzucić w Wolframa i...
A dupa.
Wolfram nie pozwala na wpisywanie tak długich wyrażeń.
Trzeba jakoś inaczej.
Napiszmy sobie prościutki skrypt w Pythonie:
from math import pi, sin, cos
import matplotlib.pyplot as plt
import numpy as np
def pole(t, r1, r2, r3, as1, as2, as3):
x1=r1*cos(2*pi*t/as1)
y1=r1*sin(2*pi*t/as1)
x2=r2*cos(2*pi*t/as2)
y2=r2*sin(2*pi*t/as2)
x3=r3*cos(2*pi*t/as3)
y3=r3*sin(2*pi*t/as3)
l1=((x2-x1)**2+(y2-y1)**2)**0.5
l2=((x2-x3)**2+(y2-y3)**2)**0.5
l3=((x3-x1)**2+(y3-y1)**2)**0.5
s = (l1+l2+l3)/2
rv=(s*(s-l1)*(s-l2)*(s-l3))**0.5
if isinstance(rv, complex):
rv=0
return rv
x = np.arange(0, 10, 0.001)
y = []
for t in x:
y.append(pole(t, 3, 4, 5, 3, 4, 5))
axes = plt.gca()
axes.set_ylim([0,20])
plt.plot(x, y)
plt.show()Funkcja licząca pole trójkąta w zależności od czasu przyjmuje siedem parametrów: czas (t), trzy odległości od słońca (r1, r2, r3) oraz trzy okresy obrotu wokół słońca (as1, as2, as3). Najpierw wyliczamy sobie współrzędne wierzchołków (x1,x2,x3,y1,y2,y3), potem długości boków oraz połowę obwodu (l1,l2,l3,s), a na koniec liczymy wynik rv ze wzoru Herona oraz całkiem znienacka sprawdzamy, czy nie wyszła nam liczba zespolona (niestety, zaokrąglenia sporadycznie wrzucają pod pierwiastek liczbę ujemną - bardzo, bardzo małą, ale jednak) i wtedy zamieniamy ją na zero.
Wynik?

Po najechaniu myszą na dzióbek w okolicach ósemki odczytujemy, że najbliższe takie wydarzenie będzie miało miejsce za 7.8 lat.
Gotowe!
Yyyy... na pewno?
Otóż nie. Nie gotowe. Przecież wyraźnie napisałem, że w zagadce jest haczyk.
Nigdzie nie pisze przecież, że planety krążą w tą samą stronę. Może być tak, że A i B kręcą się w lewo, a C - w prawo. Albo na odwrót.
Trzeba zatem sprawdzić wszystkie możliwości (po wyeliminowaniu symetrii są trzy). A więc zmieniamy linijkę mówiącą:
y.append(pole(t, 3, 4, 5, 3, 4, 5))na:
y.append(pole(t, 3, 4, 5, -3, 4, 5))potem na:
y.append(pole(t, 3, 4, 5, 3, -4, 5))i wreszcie na:
y.append(pole(t, 3, 4, 5, 3, 4, -5))Sprawdzamy każdy z powstałych w ten sposób wykresów i okazuje się, że najkrócej będziemy czekać jeżeli planeta B będzie się kręcić w kierunku przeciwnym do planet A i C:
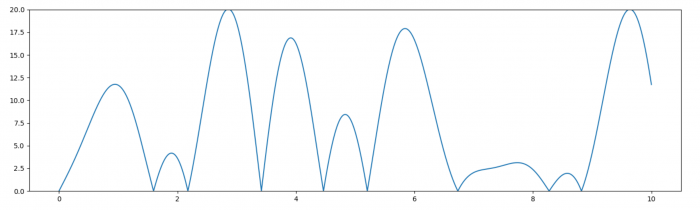
Zawężamy zakres do lat 1-3...
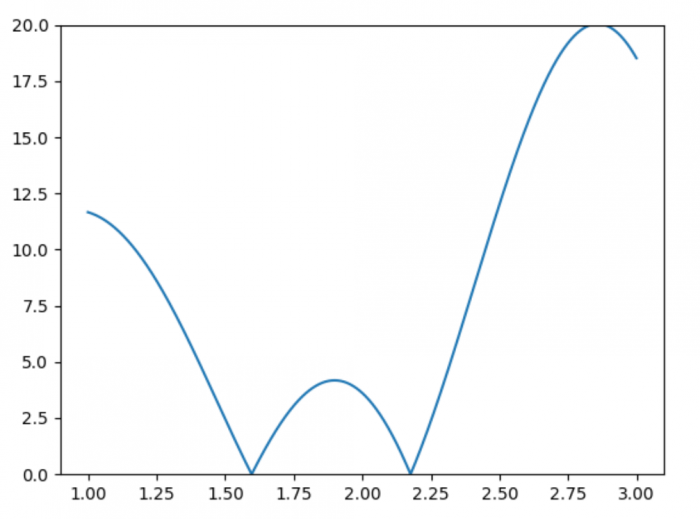
... i się okazuje, że najbliższy moment, kiedy planety będą na jednej linii nastąpi za około 1.6 lat. I to jest ostateczna odpowiedź.
Jaki to będzie układ?
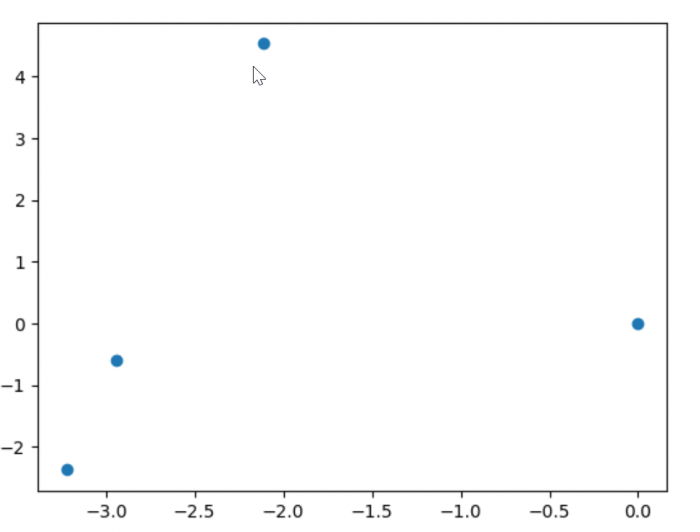
Kod generujący ostatni obrazek:
from math import pi, sin, cos
import matplotlib.pyplot as plt
odleglosci = [3, 4, 5] # promienie orbit w jednostkach astronomicznych
czasy_obiegu = [3, -4, 5] # w latach
predkosci_katowe = [2*pi/czasy_obiegu[x]
for x in range(3)] # w radianach na rok
def pozycja_planety(n, t):
# pozycja [x,y] planety numer n po czasie t (uwaga: planety numerowane od 0)
kat = t * predkosci_katowe[n]
return [odleglosci[n]*cos(kat), odleglosci[n]*sin(kat)]
def pole_trojkata(w1, w2, w3):
# w1, w2, w3: wierzchołki [x, y]
# wzór Herona: pole = sqrt(s*(s-a)*(s-b)*(s-c))
# gdzie: s to połowa obwodu (a+b+c)/2,
# a, b, c - długości boków
d1 = ((w1[0]-w2[0])**2 + (w1[1]-w2[1])**2)**0.5
d2 = ((w2[0]-w3[0])**2 + (w2[1]-w3[1])**2)**0.5
d3 = ((w3[0]-w1[0])**2 + (w3[1]-w1[1])**2)**0.5
s = (d1+d2+d3)/2
rv = (s*(s-d1)*(s-d2)*(s-d3))**0.5
if isinstance(rv, complex):
rv=0
return rv
t=0
dt=0.00001
while t<5:
t += dt
pp0 = pozycja_planety(0, t)
pp1 = pozycja_planety(1, t)
pp2 = pozycja_planety(2, t)
pt = pole_trojkata(pp0, pp1, pp2)
if pt <= 0.0001:
print([t, pp0, pp1, pp2])
plt.scatter([0,pp0[0],pp1[0],pp2[0]], [0,pp0[1],pp1[1],pp2[1]])
plt.show()
A jak Wam poszło?
Hmmm. Jak by to...
1Pierwszy odezwał się Tywan, który z góry wyjaśnił, że jego rozwiązanie obejmuje również gwiazdę, a więc szukał po ilu latach wszystkie cztery ciała niebieskie ustawią się w jednej linii (a przecież nie o to pytał Król). Wyszło mu - z odrobiną trygonometrii - 30 lat, co ma sens, bo jest to najmniejsza liczba podzielna jednocześnie przez 3, 4 i 5. Rzecz jasna, odpowiedzi nie zaliczam.
2Tego samego dnia późnym popołudniem swoje rozwiązanie nadesłał Butter. Jemu też wyszło 30, po całkiem podobnych obliczeniach. Jak już nadmieniłem powyżej, obliczenia są zasadniczo poprawne, z wyjątkiem początkowych założeń. Też nie zaliczam 🙂
3Całkiem pod wieczór odezwał się Cichy Fragles, który jako pierwszy nadesłał rozwiązanie dla trzech planet - niestety, nie wziął on pod uwagę, że mogą one krążyć w przeciwnych kierunkach, więc wyszło mu 7.8 - nieźle, jest postęp, ale to jeszcze nie to. Nie zaliczam.
4Kwadrans po Cichym swoje rozwiąznie nadesłał Waldek, który jednak poszedł na łatwiznę i wyliczył 30 lat, podobnie do Tywana i Buttera. Szkoda, liczyłem na Waldka jako Naczelnego Rozwiązywacza. To pewnie przez te upały 😉
5Nazajutrz wieczorem, na trzy godziny przed upływem terminu nadsyłania rozwiązań, Waldek podszedł do tematu raz jeszcze. Ucieszyłem się, że może rozgryzł, ale nie. Dodał tylko pominięty wcześniej wariant z planetami ustawionymi po przeciwnych stronach słońca, tzn Zendora. Wariant, który niczego nie zmienił.
Tym samym po raz pierwszy w historii Ignormatyka mamy zagadkę z odpowiedziami, ale bez zwycięzcy. Najbliżej rozwiązania był Cichy, który może sobie z tej okazji wystrugać niewielki medalik z rzodkiewki, który zaraz potem skroi na kanapkę i nie będzie się nim za bardzo chwalił 😀
A co to za jednostka miary „rok”?
A czort ich tam wie w tych innych kosmosach. Grunt, że wszyscy używają tej samej jednostki, a jak się ona ma do częstotliwości nadsubtelnego przejścia w atomach cezu 133 to już jak Marysia woli 🙂
Podstępny Gospodarzu, jak widać największym hakiem było sformułowanie samego pytania :-(. Fakt, że jest ono jednoznaczne, ale w kontekście poprzedzającego zdania łączącego linię planet z gwiazdą, skutecznie wyprowadziło czytelników w pole. Szkoda, bo przez to nikt nie zorientował się, jakie jest właściwe zadanie, a jest fajne…
Winą po połowie obarczam nieuważnych czytelników (w tym siebie) oraz zadaniodawcę, który przechytrzył.
Poprzednie zdanie miało na celu ujednoznacznienie początkowego ustawienia planet. Gdyby nie uwzględnić gwiazdy w ustawieniu początkowym, możliwości startowych byłoby nieskończenie wiele. Zadanie wciąż byłoby rozwiązywalne, ale już sporo powyżej moich skromnych progów.
Ponieważ dałem się wpuścić w maliny, to postanowiłem się zrehabilitować. Rozwiązałem to właściwe zadanie inną metodą, chyba prostszą, gdyż końcowa formuła zawiera tylko sumę trzech sinusów i można ją obliczyć za pomocą arkusza kalkulacyjnego i Wolframa też. Jakby kogo jeszcze to interesowało, to tu jest pdf do pobrania:
https://www.szybkiplik.pl/Sr3UxDC5LY
Solidna robota, i faktycznie dużo prościej od moich wypocin.
A nie zgodzę się. Było podkreślone, że zagadka jest z haczykiem, więc po pierwszym policzeniu wariantu ze wszystkimi ciałami w jednej linii szybko wpadłem i na odwrotną rotację, i na to, że słońca nie trzeba uwzględniać. Niestety, w rozjazdach byłem i na podesłanie nie starczyło mi czasu.
BTW wyszło mi 60, a nie 30 lat, niezależnie od kierunku obiegu dowolnej planety. Bug?
Imho rozwiązanie, jakkolwiek [zapewne] matematycznie poprawne, niesie ze sobą kilka ryzyk/ nieścisłości. We w weekend przypominałem sobie klasyczne pomoce naukowe z zakresu koniunkcji planet [Tomb Raider, HellBoy itp] i imho część wyników proponowanego rozwiązania nie spotka się z akceptacją kapłanów i projektantów ołtarzy ofiarnych.
Wynikiem może być sytuacja, kiedy któraś z planet znajduje się po drugiej stronie Zendora – w takim przypadku składanie ofiar to marnotrawstwo cennych zasobów [dziewic(ów)]. żaden szanujący się kapłan nie przyłoży noża do czegoś takiego.
Nie wspomnę też [co niniejszym czynię], że moje [i Tywana] rozwiązanie jest zgodne z definicją https://pl.wikipedia.org/wiki/Koniunkcja_(astronomia). Co prawda, specyfikacja zadania nie używała tego słowa, ale wyżej wspomniany materiał dowodowy zawsze.
Dowolne rozwiązanie będzie zgodne z *jakąś tam* definicją 🙂