Pogubione kaczuszki: rozwiązanie zagadki

https://xpil.eu/onz 📋

W odróżnieniu od większości prezentowanych tu zagadek, które mogą wyglądać groźnie, ale prędzej czy później okazuje się, że rozwiązanie jest względnie proste (pod warunkiem, że wpadniemy na właściwy pomysł), tutaj jest na odwrót: zagadka brzmi dość prosto, jednak znalezienie jej analitycznego rozwiązania jest nietrywialne.

Chociaż - jak pokazał Krzysiek - nie niemożliwe.

Oczywiście można zawsze próbować przeprowadzić symulację i sprawdzić wyniki. Ja tę zagadkę "rozwiązałem" właśnie w ten sposób (w Excelu) i wyszło mi, że dwie kaczuszki spotkają się średnio po pięciu minutach a trzy - po dziewiętnastu. Nie będę tu teraz przedstawiał mojego symulacyjnego karkusza bo się go trochę wstydzę (dużo w nim skrótów myślowych oraz kilka miejsc, które musiałem zadrutować lub połączyć paskudnym węzłem ze sznura od snopowiązałki), ale przynajmniej wiedziałem czego się spodziewać. Pi x oko.

A jak ten problem policzyć?

Trzeba zacząć od tego, że system, w ramach którego poruszają się nasze nieszczęsne kaczki, to proces Markowa.

Nota bene o procesach Markowa na tym blogu już kiedyś było, przy okazji generatorów losowego spaceru: https://xpil.eu/lancuchy-markowa/

Jest to proces pochłaniający (ang: absorbing) ponieważ kończy się po osiągnięciu jednego z dziewięciu stanów końcowych (tj. w sytuacji, kiedy obydwie kaczki znajdą się na tym samym kamieniu) - innymi słowy posiada stan (i to nie jeden), z którego układ już nie wychodzi.

Jest to de facto łańcuch Markowa czyli proces Markowa o czasie dyskretnym: rzeczy wydarzają się co sekundę, kaczki po każdym kroku znajdują się w konkretnym stanie, a sama zmiana stanu z N na N+1 jest pomijalnie krótka.

Przyjrzyjmy się teraz procesowi nieco bliżej.

Po pierwsze widać, że kaczki nigdy nie znajdą się na sąsiednich polach (sąsiednich w pionie lub w poziomie). Zawsze będą względem siebie albo pod skosem, albo - jeżeli znajdą się w jednym rzędzie lub kolumnie - będą rozdzielone jednym pustym kamieniem.

To dość mocno zawęża nam możliwe stany procesu: mamy tylko szesnaście możliwych układów:

Po drugie zaś możemy zredukować powyższych szesnaście możliwości do zaledwie pięciu, ponieważ prawdopodobieństwo przejścia ze stanu numer 1 (górny lewy róg) do stanu numer 2 (górny wiersz, druga kolumna) jest takie samo jak stanu numer 4 (górny prawy róg) do stanu numer 5 (drugi wiersz, pierwsza kolumna) i tak dalej. Tym samym mamy następujące stany, w których może znajdować się układ:

Dwa specjalne stany, które dodałem do listy, to stan początkowy (obydwie kaczki siedzą na środkowym kamieniu) oraz stan końca gry (obydwie kaczki siedzą na tym samym kamieniu). Różnica między tymi stanami jest taka, że ze stanu początkowego (0) układ musi przejść w jeden z dopuszczalnych stanów 1-6, natomiast ze stanu końca gry (6) układ już nie wychodzi.

No dobra. Wiemy w jakim stanie może znajdować się nasz układ kaczki-kamienie-staw, kolejnym krokiem jest wykombinowanie prawdopodobieństw, z jakimi układ może przejść z jednego stanu w drugi:

Przy okazji zauważamy, że suma prawdopodobieństw w każdym wierszu powyższej tabelki wynosi jeden: każda kaczka gdzieś musi się przemieścić po upływie minuty.

Jeżeli ktoś chciałby sobie rozrysować powyższą macierz przekształceń w postaci grafu, w którym węzły reprezentują poszczególne stany układu, a krawędzie prawdopodobieństwa przejścia między nimi - wyglądałby on mniej więcej tak:

Dla zainteresowanych: to jest kod powyższego grafu zapisany w języku DOT:

digraph g{
0->1 [label="1/4"]
0->4 [label="1/2"]
0->6 [label="1/4"]
1->2 [label="2/9"]
1->3 [label="4/9"]
1->5 [label="2/9"]
1->6 [label="1/9"]
2->1 [label="1/4"]
2->4 [label="1/2"]
2->6 [label="1/4"]
3->1 [label="1/4"]
3->4 [label="1/2"]
3->6 [label="1/4"]
4->2 [label="2/9"]
4->3 [label="4/9"]
4->5 [label="1/9"]
4->6 [label="2/9"]
5->1 [label="1/2"]
5->4 [label="1/2"]
6->6 [label="1"]
}

A teraz zanurzymy się w ciemnym świecie macierzy. Albowiem bez macierzy łańcuchy Markowa rozwiązuje się nader niewygodnie.

Żeby nie przedłużać, tu mamy link do gotowca z Wikipedii, który opowiada nam najpierw ogólnie o pochłaniających łańcuchach Markowa, a potem podaje konkretne wzory na policzenie tego i owego (w tym również na średnią oczekiwaną liczbę kroków od zadanego stanu początkowego do stanu "pochłoniętego").

(niestety nie chciało mi się szukać polskojęzycznej wersji tego artykułu - może któryś z Czytelników ma akurat coś pod ręką?)

Podstawiając dane z naszej macierzy przekształceń do wzorów podanych w powyższym artykule (a więc: najpierw wyznaczamy macierz fundamentalną N a następnie mnożymy ją przez kolumnę jedynek) dostaniemy na wyjściu: (KLIK)

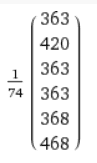
Powyższe rozwiązanie należy odczytać tak, że ze stanu 0 do stanu 6 przejdziemy średnio po 363/74=4.9 krokach. A więc moja bałaganiarska symulacja w Excelu podała poprawne rozwiązanie (z dokładnością do części całkowitej).

A co z trzema kaczuszkami?

Przy większej liczbie kaczek proces się komplikuje (i to wykładniczo), powiem więc tylko tyle, że średnia oczekiwana liczba minut dla trzech kaczek wynosi 18.4 (tu mój symulator podał 19). Dla czterech kaczek jest to 67 minut, dla pięciu - 237, dla sześciu ponad 800 i tak dalej. Przy dwunastu kaczkach czas potrzebny na ponowne spotkanie zwiększy się do około dwóch lat, a przy stu czterdziestu - przekroczy aktualny wiek Wszechświata.

Oczywiście przedtem wyparuje staw, kaczki, kamienie i matematyka, ale o tym sza.

https://xpil.eu/onz 📋