Zagadka polegała na znalezieniu najkrótszej możliwej trasy startującej z wierzchołka A trójkąta równoramiennego ABC z kątem przy wierzchołku B = 15° takiej, żeby dojść do boku BC, zawrócić i dojść do boku AB, jeszcze raz zawrócić i dojść do boku BC.
Można to zadanie rozwiązać na kilka sposobów. Najbardziej logiczne wydaje się skonstruowanie funkcji długości trasy w zależności od dwóch kątów, pod jakimi rozpoczynamy każdą część spaceru (ostatni, trzeci kąt jest zdeterminowany kątem prostym u celu), a następnie skorzystanie z rachunku różniczkowego w celu znalezienia minimum.
Można też spróbować znaleźć rozwiązanie przybliżone metodą Monte Carlo.
Ale to wszystko sposoby wymagające dość zaawansowanej wiedzy (matematycznej bądź komputerowej). Da się prościej.
Dużo prościej.
Przyjrzyjmy się co się wydarzy jeżeli odbijemy sobie nasz trójkąt ABC w lusterku, dwa razy:
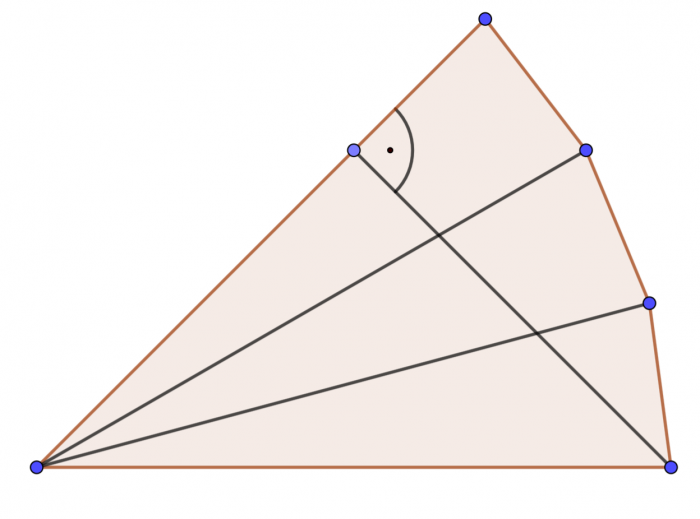
Okazuje się, że naszą podróż od dolnego prawego wierzchołka do przeciwległej krawędzi, z powrotem i znów z powrotem można sobie rozrysować na takich lustrzanych odbiciach jako odcinek dotykający drugim końcem boku ostatniego trójkąta pod kątem prostym.
A skoro kąt przy wierzchołku miał 15°, potrojony wyniesie 45°, czyli z definicji sinusa wychodzi nam od razu, że długość trasy to $$\frac{\sqrt{2}}{2}$$ czyli mniej więcej 0.7071. Mnożymy przez sto (bo tyle wynosi, w metrach, długość boku ogrodu) i mamy odpowiedź: najkrótsza trasa ma 70 metrów i 71 centymetrów.
A jak Wam poszło?
1Nagrodę za pierwszą nadesłaną odpowiedź otrzymuje tym razem Butter, którego dość zaawansowane bazgroły, których kompletnie nie zrozumiałem zaowocowały wynikiem 78 metrów i 32 centymetry. Nie zaliczam.
2Pół godzinki potem swoje rozwiązanie nadesłał Cichy, który odbił wyjściowy trójkąt dwa razy względem dłuższego boku i narysował odcinek prostopadły o długości 100 * 0.7071. Gratuluję wygranej!
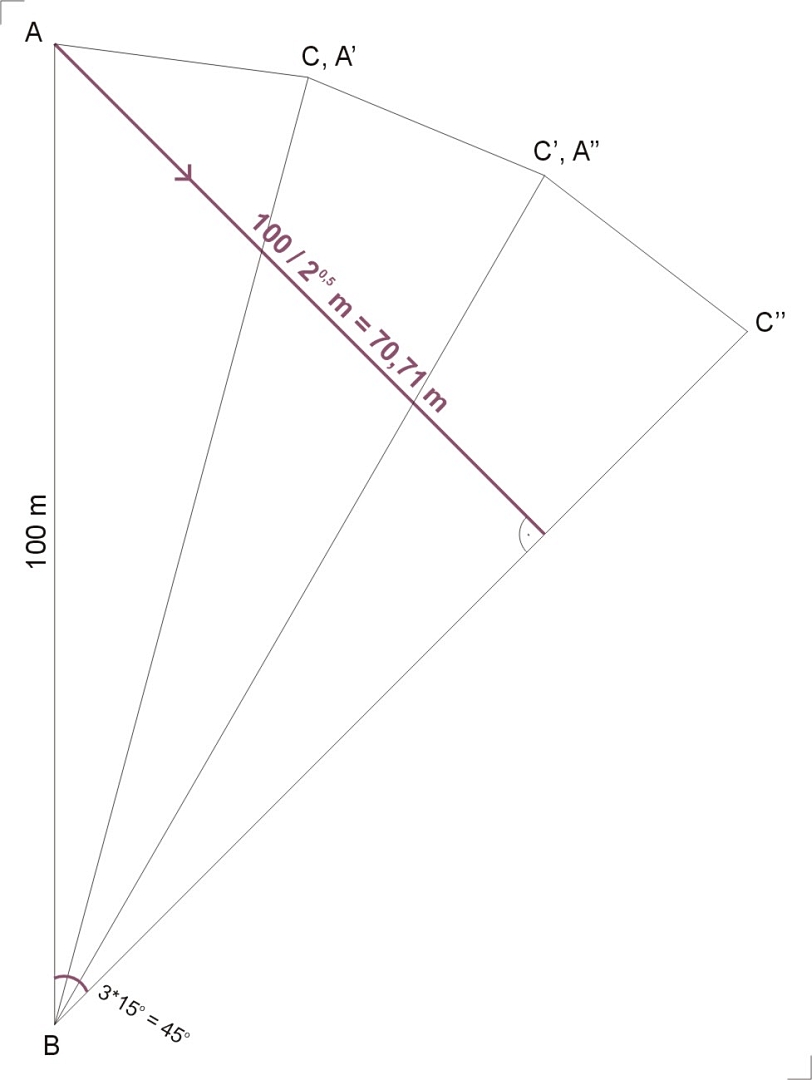
Zamiast się odbijać od boków, możemy odbijać trójkąt względem odpowiedniego boku, tworząc w ten sposób wachlarzyk z trzech trójkątów połączonych długim bokiem i stykających się ostrymi wierzchołkami w jednym punkcie - wtedy nasz zygzak staje się równoważny z drogą z punktu A do przeciwnego boku trój-trójkąta. Najkrótsza droga będzie oczywiście odcinkiem prostopadłym do rzeczonego boku, a że kąt u dolnego wierzchołka wyniesie 3 * 15 = 45 stopni, to i wyjście z punktu A musi być pod takim samym kątem - otrzymujemy więc trójkąt prostokątny, gdzie przeciwprostokątna ma sto metrów, a długość przyprostokątnej wynosi sto pierwiastków z dwóch przez dwa, czyli według kalkulatora 70m 71cm.
-- Cichy, styczeń 2022
3Nazajutrz odpowiedź nadesłał Waldek i - po waldkowemu - pozamiatał parkiet za pomocą tego oto obrazka:
4Zaraz po Waldku odezwał się Rozie, któremu wyszło ciut ponad 50 metrów, z następującym wzorem: https://www.wolframalpha.com/input/?i=cos15+degreessin15+degrees++sin15+degrees+100. Nie rozumiem kompletnie skąd się to wzięło, ale na moje oko żeby pokonać wymaganą trasę w 50 metrów trzeba by chyba nieco zakrzywić przestrzeń... Nie zaliczam.
5Piątym rozwiązującym był Tywan, który poszedł drogą dookoła i prawie trafił. Napisał sobie trochę kodu w C++; założył też (całkiem słusznie), że ostatni odcinek spaceru musi być prostopadły do linii docelowej - wyszło mu w wyniku 71.43 metrów, czyli około pół metra więcej niż rozwiązanie optymalne. Chociaż nie zaliczam, to uchylam kapelusza za nietypowe podejście.
6Rafał dostaje medal za uczestnictwo. Rozpisał on całkiem szczegółowo wariant spaceru, w którym za każdym razem wybieramy kierunek prostopadły do boku, do którego się w danym momencie zbliżamy - z odrobiną sinusów i kosinusów wyszło mu 75 metrów i 3 centymetry. Obliczenia poprawne. Szkoda tylko, że do błędnego założenia. Nie zaliczam.
Najkrótsza droga do odcinka musi się z nim łączyć pod kątem prostym. Czyli startuję z wierzchołka A i idę prostopadle do odcinka CB itd. Żeby obliczyć ten pierwszy odcinek spaceru trzeba najpierw obliczyć długość odcinka AC i w tym celu z wierzchołka B wypuszczam wysokość trójkąta, która dzieli kąt przy wierzchołku B na dwa równe kąty a odcinek AC na dwa równe odcinki (cały trójkąt ABC jest równoramienny), a później już z górki: obliczam długość AC AC = (sin (7,5s) * 100) * 2 = 26,1053 obliczam spacer1 S1 = sin(82,5s) * 26,1053 = 25,882 obliczam odcinek BC skrócony BCs = 100 - (cos(82,5s)26,1053)=96,5927 obliczam spacer2 S2 = sin(15s)96,5927=25 obliczam odcinek BA skrócony BAs = 25 / tg(15s)=93,3014 obliczam spacer3 S3 = sin(15s)*93,3014=24,1482 S1+S2+S3 = 25,882+25+24,1482=75,03
-- Rafał, styczeń 2022
7Rzast był siódmym zgadującym - niestety podążył on tym samym tropem co Rafał i tyle samo mu wyszło. Nie zaliczam.
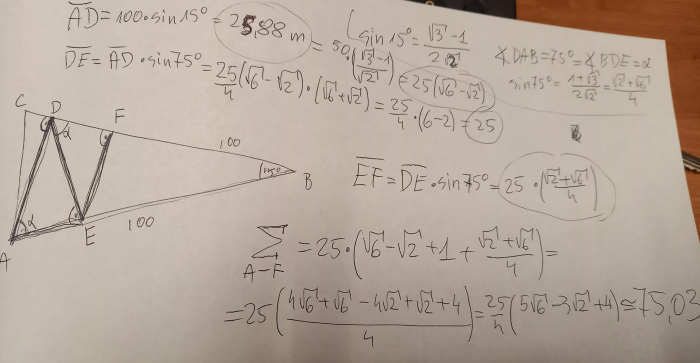
Ech… znowu to samo…
Nie trać animuszu. Kiedyś się uda 🙂
Tylko tak jakby zwycięska trasa nie spełnia warunków, że zacytuję wieszcza: „od dolnego prawego wierzchołka do przeciwległej krawędzi, z powrotem i znów z powrotem”.
Jak z powrotem, to z powrotem, do punktu A, nieprawdaż. 5 kilo cukru i do domu. I do domu!
We wpisie z odpowiedzią zastosowałem skrót myślowy. Oryginalna treść zadania objaśnia bardziej szczegółowo o co biega.
Żadnych kompromisów – Corel.
To ja powiem, że poszedłem tym samym tropem, co Rzast i Rafał, czyli przyjąłem, że spacerowicz odbywa drogę między krawędziami zawsze najkrótszą drogą. Tyle, że dodatkowo tylko tam i z powrotem, czyli dwa razy, nie trzy.
Cóż, tak to jest jak się w biegu na telefonie i czyta, i rozwiązuje. :-/