Dzięki komentarzowi Borysa pod wpisem z zagadką znamy już prawidłową odpowiedź...
Okazuje się, że gra nie opłaca się. Albo raczej - opłaca się, ale prowadzącemu. W końcu kasyno zawsze wygrywa, prawda?
Jak jednak do tego dojść?
Symulacja jest prościutka i przedstawię ją na końcu. Zacznijmy jednak od rozważań teoretycznych (nie będzie zbyt trudno, proszę się nie martwić na zapas)
Po pierwsze zauważmy, że po każdym rzucie mamy cztery możliwe wyniki (zdarzenia):
- Z1: Trafiliśmy 3 razy
- Z2: Trafilismy dokładnie 2 razy
- Z3: Trafiliśmy dokładnie 1 raz
- Z4: Nie trafiliśmy ani razu
Każdy z tych wyników ma powiązaną:
- kwotę wygranej (odpowiednio: €30, €20, €10, -€10) oraz
- prawdopodobieństwo wystąpienia (oznaczmy sobie te cztery prawdopodobieństwa jako \(P_1, P_2, P_3, P_4\))
Wartość oczekiwana wygranej przez nas kwoty to suma prawdopodobieństw poszczególnych zdarzeń przemnożonych przez kwotę wygranej dla każdego zdarzenia, czyli:
\(W_O = €30 P_1 + €20 P_2 + €10 P_3 - €10 P_4\)(gdzie \(W_O\) to Wartość Oczekiwana)
Pozostaje teraz wyznaczyć prawdopodobieństwa \(P_1 - P_4\) i dostaniemy odpowiedź.
Jakie jest prawdopodobieństwo, że wszystkie trzy kości pokażą wskazaną przez nas liczbę?
Dla jednej kości jest to 1/6. Szansa, że to samo wypadnie na trzech kościach to (1/6)^3
\(P_1 = 1/216\) \(P_4\) oznacza, że nie trafiliśmy ani razu. Spudłowanie dla jednej kostki to 5/6, dla trzech - (5/6)^3\(P_4 = 125/216\)
To były te łatwiejsze przypadki.
\(P_2\) i \(P_3\) wymagają odrobinę więcej pomyślunku. \(P_2\) - jakie jest prawdopodobieństwo, że trafiliśmy dokładnie dwa razy?Na kostce numer 1 szansa trafienia to 1/6.
Żeby trafić dodatkowo kostką numer 2 mamy szansę (1/6)^2 - ale pamiętajmy, że należy wyeliminować wariant, kiedy trafiliśmy również na kostce numer 3.
Na trzeciej kostce musi więc być pudło (szansa: 5/6). Tym samym prawdopodobieństwo, że dostaniemy dwa trafienia i jedno pudło wynosi (1/6)^2*(5/6).
Poprawnie?
Nie!
Powyższe wyrażenie należy jeszcze przemnożyć przez trzy.
Dlaczego tak?
Ponieważ "spudłowana" kostka może mieć numer 1, 2 lub 3
Innymi słowy mamy tu trzy niezależne od siebie zdarzenia, które "pasują" - ich prawdopodobieństwa należy do siebie dodać.
A więc \(P_2\) = 3 * (1/6)^2 * (5/6)
\(P_2 = 5/72\)
\(P_3\) wyliczymy podobnie - tylko tym razem mamy dwa pudła i jedno trafienie:
\(P_3\) = 3 * (5/6)^2 * (1/6)
\(P_3\) = 25/72
Zanim pogalopujemy dalej sprawdźmy, czy nasze cztery prawdopodobieństwa sumują się do jedynki (powinny, skoro są od siebie niezależne i pokrywają wszystkie możliwe wyniki losowania):
\(P_1 + P_2 + P_3 + P_4 = 1/216 + 125/216 + 5/72 + 25/72 = ...\)https://duckduckgo.com/?q=1%2F216%2B125%2F216%2B5%2F72%2B25%2F72&t=hp&ia=calculator
... 1, czyli na razie wszystko ładnie, pięknie.
Pozostaje wyliczenie wartości oczekiwanej:
\(W_O = 30 P_1 + 20 P_2 + 10 P_3 - 10 P_4\) \(W_O = 30 * (1/216) + 20 * 5/72 + 10 * 25/72 - 10 * 125/216 = ...\)https://duckduckgo.com/?q=30*(1%2F216)%2B20*5%2F72%2B10*25%2F72-10*125%2F216&t=hp&ia=calculator
... -0.78703703703
Jak widać, po dłuższym graniu okaże się, że jesteśmy w plecy średnio jakieś 79 centów na jednej grze. Niewiele, ale wystarczy, żeby kasyno wygrało 😉
Czy możemy jakoś zweryfikować ten wynik doświadczalnie?
Moglibyśmy wziąć kostki i nimi rzucać, ale można szybciej.
Uruchamiamy Excela...
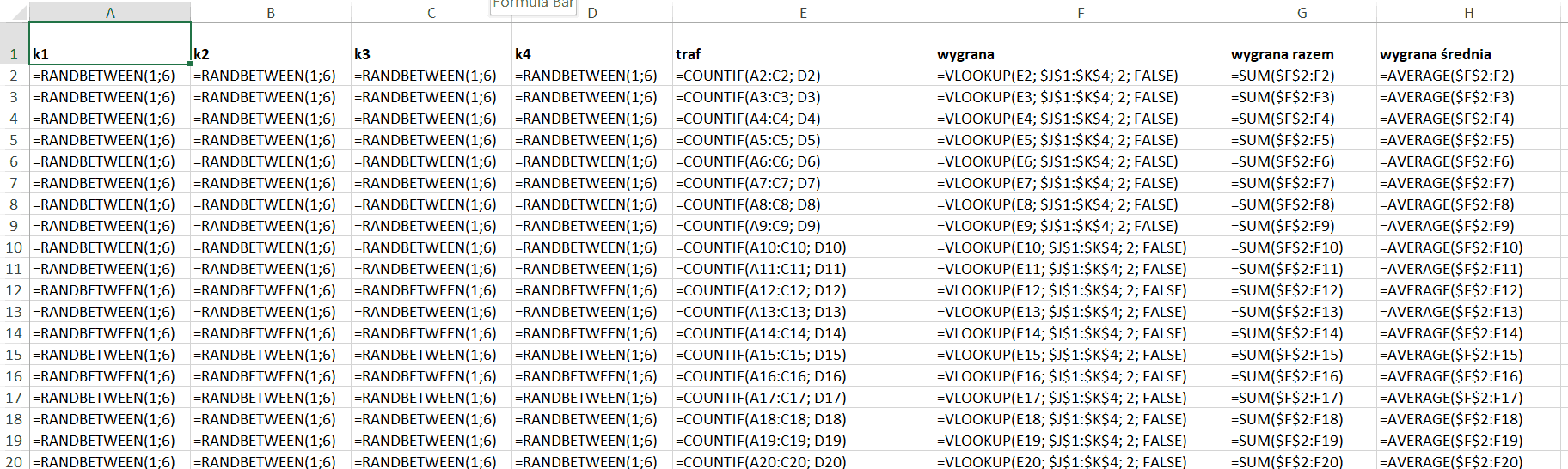
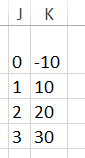


Jak widać po 20,000 gier przegraliśmy 15,250 Jerzych, czyli średnio 76 centów na partię. Prawie idealna zgodność z wynikiem teoretycznym.
Nie warto chodzić do kasyna...

Przeczuwałem to. Lepiej sprawdza się jagodzianka na kościach.