1
Dzisiejszą serię interesujących linków zaczniemy od gry w statki. Ładnie zrobiona. Szkoda tylko, że wersja uproszczona jest zbyt prosta, a wersja utrudniona - zbyt trudna, przynajmniej jak na moje trzy na krzyż neurony. Ale z nudów można poklikać.
Nota bene strona domowa Autora zawiera dużo więcej ciekawostek i łamigłówek - bardzo polecam.
2

Liczby wampirze ("wampirowe"? "wampirne"?) to takie liczby całkowite o parzystej liczbie cyfr (N), które można przedstawić jako iloczyn dwóch liczb N/2-cyfrowych zbudowanych z N cyfr oryginalnej liczby (dowolnie poprzestawianych). Na przykład 1260 = 21*60, albo 1395=15*93.
3

Chcesz sobie poćwiczyć LaTeX-a? Proszę bardzo.
4

W maju tego roku Matt pobił rekord Guinnessa produkując największą (w sensie liczby elementów) kostkę Rubika: 34x34x34. W artykule opisano też historię poprzednich rekordów oraz trochę technicznych szczegółów związanych z budowaniem coraz większych kostek.
5

Robot, który potrafi załadować / wyładować pranie do / z pralki. Wyjęte pranie potrafi porozwieszać na suszarce. Wyschnięte - poskładać. Póki co to tylko prototyp. Powoli, ale nieubłaganie zbliżamy się do Tragedii Pralniczej 🙂
6

Jeżeli dać wszystkim małpom na świecie po maszynie do pisania oraz bardzo dużo czasu, któraś kiedyś napisze komplet dzieł Szekspira. Prawda?
7

Brian pojawia się w moim zestawieniu dość często - gość umie w astronomię i potrafi przekazać skomplikowane idee w sposób strawny dla zwykłych zjadaczy bitów. Tym razem opowiada o efekcie wleczenia inercjalnego układu odniesienia (po angielsku dużo prościej: frame dragging, ale przecież nie powiemy "ciągnięcie ramki", prawda?), który nieco rozjaśnia kwestie kwazarów.
P.S. Tuż przed publikacją tego wpisu zajrzałem jeszcze raz na stronę Briana i znalazłem tam ten oto artykuł, omawiający hipotezę horyzontu Cauchy'ego, hipotetycznej struktury znajdującej się wewnątrz sfery Schwartzschilda. Być może stoimy u progu teorii będącej dla einsteinowskiej fizyki relatywistycznej tym, czym była ona dla fizyki newtonowskiej.
8

Jeżeli wydaje ci się, Czytelniku sympatyczny, że umisz w kumputery a zwłaszcza w obsługę tekstów (aka stringów, aka łańcuchów znaków), zanim klikniesz poniższy link, spróbuj odpowiedzieć na następujące pytanie: czy istnieje w "komputerowym alfabecie" znak, który może występować zarówno w formie "wielkiej litery" jak też "małej litery" (jak na przykład "D" i "d", albo "W" i "w"), ale sam w sobie nie jest ani małą literą, ani wielką literą?
Okazuje się, że jak najbardziej - i to niejeden. Głównie dzięki Węgrom i innym nacjom z południa Europy.
9
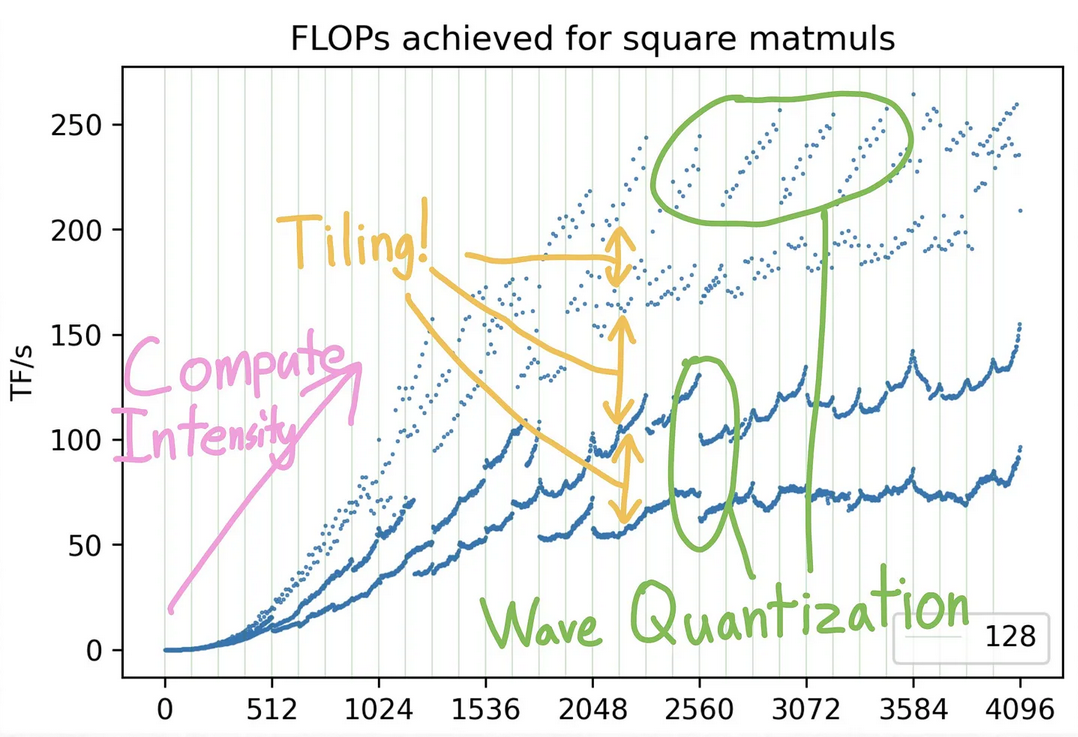
Skoro od kilku lat wszyscy trąbią o LLM-ach, a LLM-y jak powszechnie wiadomo to nic innego jak wielkie, mnożące papugi, oto artykuł o tym, że w niektórzych przypadkach zwiększenie rozmiarów mnożonych macierzy może poskutkować... zmniejszeniem czasu wykonania operacji mnożenia. Kwestia rozbija się, jak się okazuje, o zarządzanie pamięcią podręczną.
10
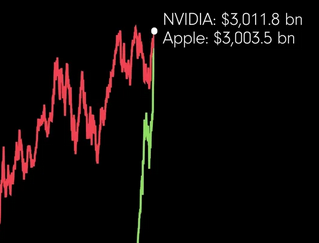
Na koniec coś ze świata wielkich finansów (bez wielkiego zaskoczenia nadal jednak pozostajemy w świecie LLM-ów... poniekąd). Otóż 6 listopada 2024 NVidia wyprzedziła Apple jako najwyżej wyceniana firma na świecie, z wyceną na poziomie 3.43 bilionów dolarów amerykańskich.
(Gwoli jasności: chodzi o nasze polskie biliony, czyli angielskie trillions, czyli miliony milionów)
Stare przyszłowie pszczół mówi: w czasach gorączki złota najlepiej zarabiają sprzedawcy łopat...
Ad 1: Pokonał mnie interfejs; nie rozumiałem oznaczeń klikniętych pól. Nie chcę mi się tłumaczyć, o co chodzi, ale chodzi o to, że tak prosta gierka powinna mieć (jeszcze) bardziej intuicyjny UX.
Ad 3: Swojego czasu szukałem edytora Markdown, który obsługiwałby składnię matematyczną i renderował ją w czasie rzeczywistym. Przetestowałem wiele różnych i okazało się, że umie to tylko Typora. Soft płatny, ale tak zgrabny, że zapłaciłem (chociaż prawie nigdy nie kupuję użytków). Szkoda, że Ghostwriter, którego interfejs podoba mi się bardziej, matematyki nie rozumie.
Ad 4: Mądrzy ludzie o zwinnych palcach twierdzą, że kostki Rubika większe niż 5x5x5 są interesujące już tylko z technicznego punktu widzenia – bo algorytm prowadzący do rozwiązania się zasadniczo nie zmienia, robi się tylko coraz bardziej skomplikowany.
Ad 7: No nie, znowu Cauchy (akurat studiuję zaocznie analizę zespoloną)? Boję się otworzyć lodówkę.
Ad 8: Trochę z innej beczki: Kiedyś szukałem glyfów, które są na pierwszy rzut nieodróżnialne od zwykłych liter łacińskich, i okazało się, że każda litera takich zamienników ma całkiem sporo. Tym sposobem tekst optycznie zupełnie zrozumiały dla człowieka można uczynić nieczytelnym dla parsującego go AI.
Ad 10: Podobno jeśli ktoś chce zbić fortunę na założeniu rejestracji, należy raczej zaproponować mu założenie firmy sprzedającej sztućce i obrusy.
> …Pokonał mnie interfejs…
Logika jest banalna: pole może być albo nieoznaczone (białe, coś jak NULL w bazie danych), albo statek (czarne), albo woda (niebieskie). Celem gry jest ustalenie położenia wszystkich pól czarnych i niebieskich, przy zadanych warunkach początkowych (niektóre czarne / niebieskie przyklejone na stałe, plus liczniki czarnych na marginesach). Puknięcie w pole zmienia stan cyklicznie: białe => niebieskie => czarne. Ponadto jeżeli liczba czarnych w danym wierszu / kolumnie zgadza się z liczbą na marginesie, puknięcie w margines wypełnia pozostałe białe pola na niebiesko, oszczędzając czasu.
> Ad 8…
Pisałem o tym kiedyś tutaj: https://xpil.eu/atak-homograficzny/
„Puknięcie w pole zmienia stan cyklicznie: białe => niebieskie => czarne”
Ale tylko przy LPM, bo w PPM masz na odwrót.
Całkiem możliwe. Gram tylko na smartfonie.
Ad 6. Była jedna taka „małpa” – Szekspir, więc powinno być pytanie nie o odtworzenie dzieł, ale prawdopodobieństwo takich samych wyników u dwóch różnych autorów.
Podobne do wyliczenia prawdopodobieństwa wytypowania przez dwóch/więcej graczy takich samych cyfr w totku i w dodatku wygrania kumulacji.
ALE: 30 marca 1994 roku padła rekordowa liczba „szóstek” w jednym losowaniu, aż 80. Wylosowano wówczas liczby: 11, 16, 23, 30, 35 i 41
Szanse na wygranie szóstki w Totka są jak 1:14M (w przybliżeniu, faktycznie odrobinę lepsze). Przy 9-10 milionach grających szansa na wygraną przez co njamniej jedną osobę to okolice 50%. Szansa, że wygra 80 osób jest przyzerowa: trzeba podnieść 0.5 do 80 potęgi, czyli wychodzi jeden do kwadryliona.
W przypadku małp i Szekspira mówimy o prawdopodobieństwie tak małym, że nawet jeżeli skopiujemy nasz Kosmos tyle razy, ile ma on atomów i przeprowadzimy niezależny eksperyment w każdym z tych kosmosów, używając wszystkich małp z całej Ziemi, przez czas potrzebny do śmierci cieplnej wszechświata i zakładając, że małpa naciska losowy klawisz raz na sekundę, to i tak się nie uda.
„Troszkę” inna skala problemu 🙂
Zenonowi też się wydawało, że Achilles nie dogoni żółwia, bo choćby zrobił 0.5 do 80 potęgi kroków… A tu niespodzianka, w matematyce nie chodzi o czas, ale o prawdopodobieństwo, a to jest i dla Achillesa i dla małp równe 1. I pozamiatane.
Z tym, że nie do końca. Przeszkodą nie do pokonania nie jest ani czas, ani rachunek prawdopodobieństwa, ale małpy. Im się nie chce naciskać klawisze losowo. Miałem kiedyś obrzydliwy filmik z szympansami obsługującymi komputer, ale gdzieś go wcięło, więc w zastępstwie tylko ugrzeczniony opis:
https://pl.wikipedia.org/wiki/Twierdzenie_o_niesko%C5%84czonej_liczbie_ma%C5%82p#Empiria
#1 bez problemu największy układ, nawet z trybie hard. Oczywiście nie za każdym razem, ale do rozwiąania.