Z grafologią wpis dzisiejszy nie ma nic wspólnego, ani z algami, ani z rytmami też nie. Jak już wiele razy wspominałem, wymyślanie tytułów do wpisów nie jest moją najmocniejszą stroną.
Uważny Czytelnik może skojarzyć zagadkę o drabince liczb pierwszych (z maja zeszłego roku), do której rozwiązania użyłem pythonowej biblioteki networkx. Oprócz standardowych operacji na grafach, biblioteka ta oferuje też kilka algorytmów rysowania grafów. Dziś chciałem pokazać czym się owe algorytmy różnią oraz w jaki sposób wyświetlić wiele wykresów na jednym (coś, z czym zawsze mam problem i muszę za każdym razem guglać).
Zaczniemy od kodu:
from sympy import isprime
import networkx as nx
import matplotlib.pyplot as plt
# oryginalny kod z rozwiązania zagadki z zeszłego roku
# wersja dwucyfrowa
digits = 2
primes = [n for n in range(10**(digits-1), 10**digits) if isprime(n)]
G = nx.Graph()
for p in primes:
G.add_node(p)
for nn in G.nodes:
a_number = str(nn)
for digit_pos in range(len(a_number)):
for digit in range(10):
candidate = a_number[:digit_pos] + str(digit) + a_number[digit_pos + 1:]
if candidate != a_number and candidate[0] != '0' and isprime(int(candidate)):
G.add_edge(nn, int(candidate))
# lista algorytmów
layouts = [
(nx.kamada_kawai_layout, {'scale': 2}), # parametr scale=2 zmniejsza szansę na pokrywanie się kółek
(nx.spring_layout, {'scale': 2}),
(nx.random_layout, {}),
(nx.shell_layout, {}),
(nx.circular_layout, {}),
(nx.spectral_layout, {}),
(nx.spiral_layout, {})
]
# lista podwykresów
fig, axes = plt.subplots(3, 3)
# zamieniamy dwywumiarową listę podwykresów na jednowymiarową,
# żeby było łatwiej odwoływać się do poszczególnych podwykresów
axes = axes.flatten()
for i, (layout, params) in enumerate(layouts):
pos = layout(G, **params)
nx.draw(G, pos, ax=axes[i], with_labels=True, node_shape='o', font_size=5, edge_color='lightgray', node_color='lightgray', width=0.5, node_size=80, linewidths=1)
axes[i].set_title(layout.__name__.replace("_layout", ""))
# usuwamy dwa ostatnie (puste) podwykresy
axes[-1].remove()
axes[-2].remove()
plt.show()
Kod zawiera komentarze, które (mam nadzieję) objaśniają co się dzieje w poszczególnych krokach. Zamiast więc omawiać teraz skrypt krok po kroku przejdę od razu do wyniku, który wygląda o, tak:
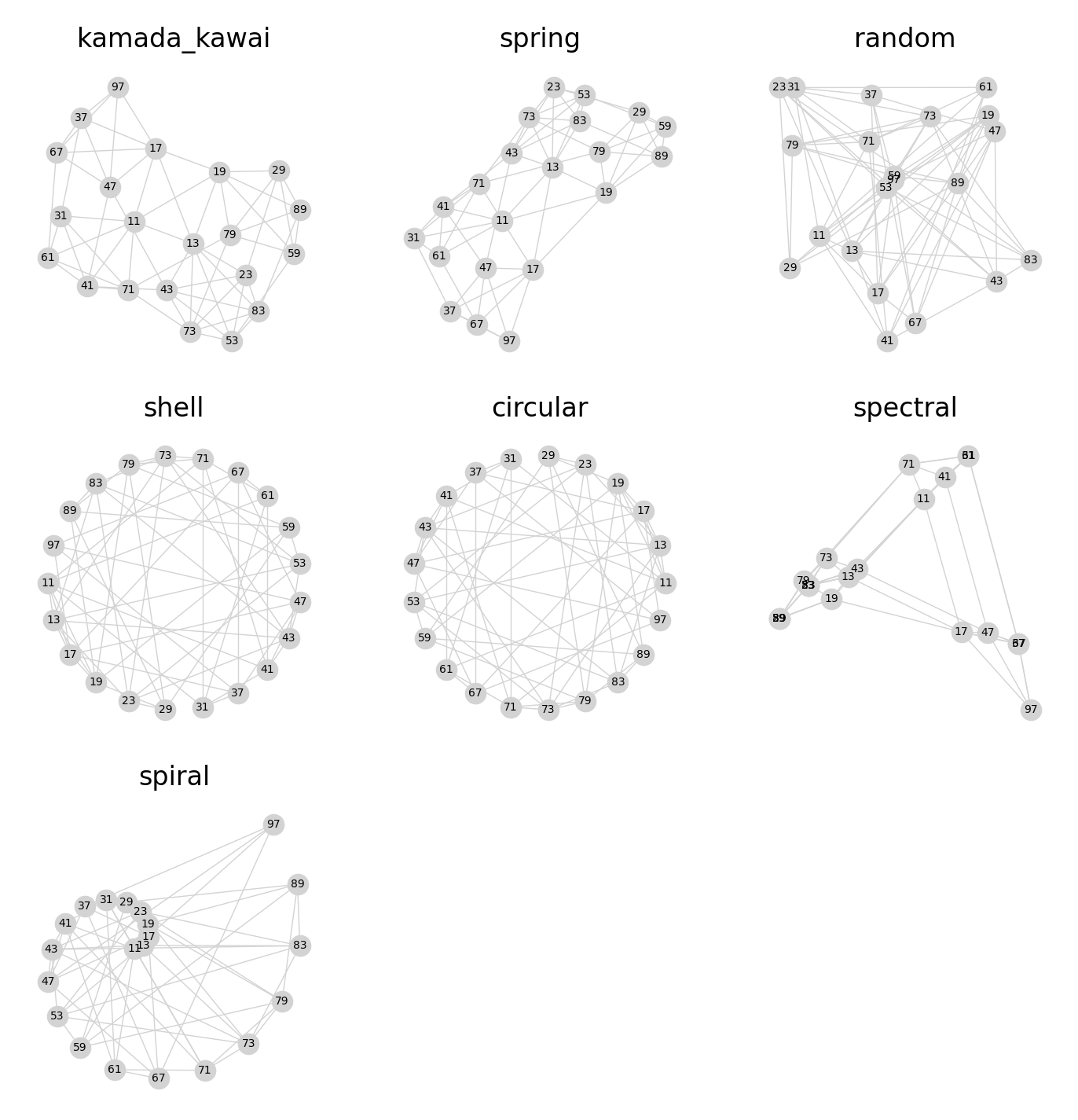
Gwoli wyjaśnienia: siedem grafów pokazanych na rysunku powyżej to jest - formalnie - jeden i ten sam graf, tylko narysowany na siedem różnych sposobów. Algorytmów rysowania grafu jest w networkx więcej (około 10 albo 11 o ile dobrze kojarzę), jednak ten konkretny graf nie nadaje się do pokazania wszystkich, dlatego ograniczyłem się do tych siedmiu.
Co można zaobserwować na podstawie powyższego obrazka?
Po pierwsze, wydaje się, że algorytmy shell i circular produkują prawie identyczny układ (w zasadzie jakby obrócić jeden z nich, dałoby się nałożyć na drugi prawie co do piksela). W rzeczywistości algorytm circular jest dużo bardziej prymitywny - zawsze układa wierzchołki grafu w pojedyncze koło - natomiast shell umożliwia zorganizowanie grafu w pierścienie, których tu jednak nie mamy, więc domyślnie zrobił jedno koło.
Po drugie, widać wyraźne podobieństwo między algorytmami spring oraz kamada_kawai - i nie bez powodu, ponieważ obydwa te algorytmy opierają się na minimalizowaniu "energii" w grafie, a więc starają się, aby było jak najmniej przecinających się krawędzi, aby długości krawędzi były w miarę możliwości równe i tak dalej. Wewnętrznie owa "energia" jest w każdym z nich reprezentowana nieco inaczej: spring operuje lokalnie, a więc traktuje każdą krawędź jak "sprężynę" dążącą do pewnej równowagi, ponadto dodaje siłę "odpychającą" między wierzchołkami. kamada_kawai natomiast jest bardziej zaawansowany i stara się zminimalizować długość krawędzi nie tylko między najbliższymi wierzchołkami, ale również między tymi połączonymi przez pośredników. Dlatego układy się jednak nieco różnią. Widać jednak, że sąsiedztwa wierzchołków są w zasadzie identyczne w obu przypadkach. Na przykład trapez złożony z wierzchołków 67-37-97-47-17 pojawia się i tu, i tam, w bardzo podobnym układzie.
Po trzecie, warto nadmienić, że w większości przypadków da się te algorytmy nieco "podrasować" w celu uniknięcia "zderzeń" wierzchołków (parametr scale - szczegóły patrz komentarze w skrypcie), jednak nie ze wszystkim. Spiral prawie na pewno wyprodukuje nakładające się wierzchołki w środku spirali, random jest losowy, więc nie mamy tu za bardzo kontroli nad układem wierzchołków i dla większych grafów nałożenia są w zasadzie gwarantowane, wreszcie spectral produkuje klastry, w których wierzchołki są ułożone na tyle gęsto, że uniknąć nałożeń też się za bardzo nie da.
Na zakończenie bonusik, czyli te same algorytmy dla liczb trzycyfrowych:
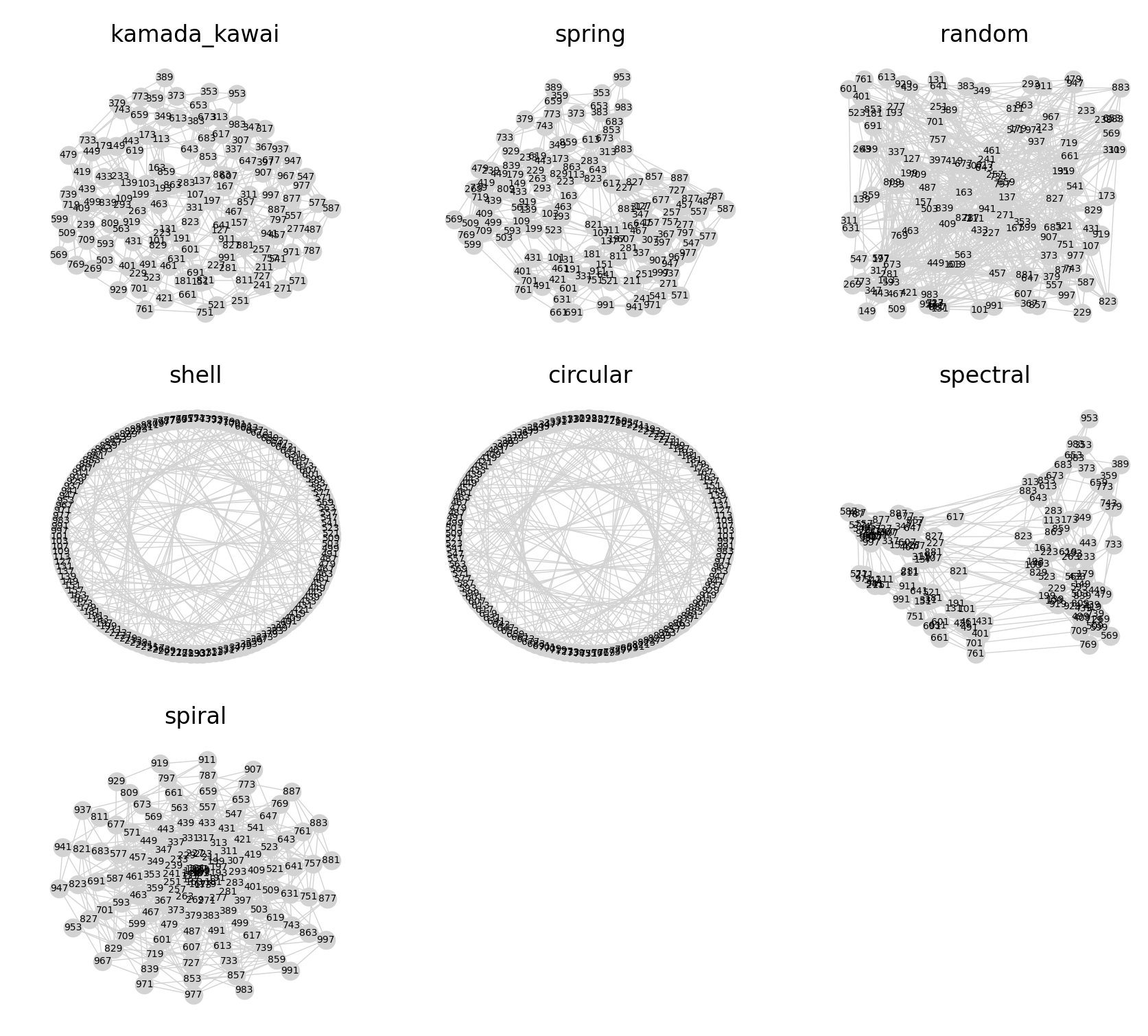
... i dla czterocyfrowych:

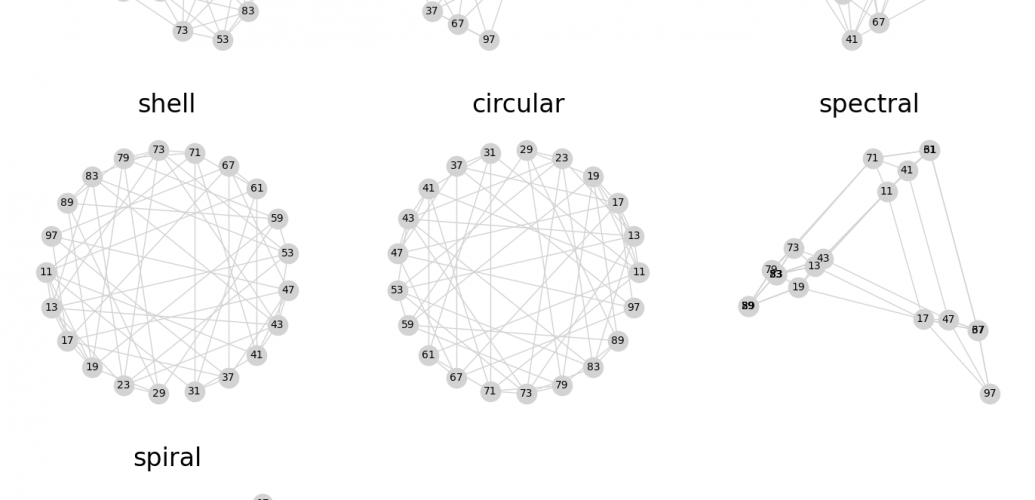
Jeżeli chcesz do komentarza wstawić kod, użyj składni:
[code]
tutaj wstaw swój kod
[/code]
Jeżeli zrobisz literówkę lub zmienisz zdanie, możesz edytować komentarz po jego zatwierdzeniu.