Mamy dwa prostokąty o bliżej nie znanych nam wymiarach. Prostokąty owe stykają się ze sobą tak, że tworzą kształt litery "L". Na przykład tak:

Albo tak:

Albo nawet tak:
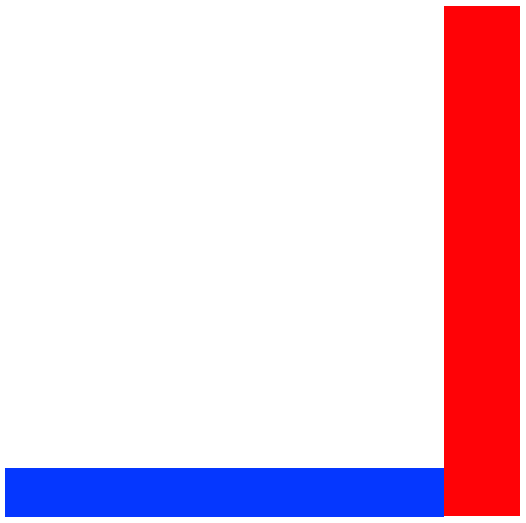
Dysponując wyłącznie liniałem (czyli linijką bez skali/podziałki) i ołówkiem należy wykreślić odcinek, który podzieli tę L-kształtną figurę na pół - "odcięte" pola powierzchni po obu stronach odcinka mają być identyczne.
Uwaga: dopuszczamy podział na trzy części, na przykład tak:
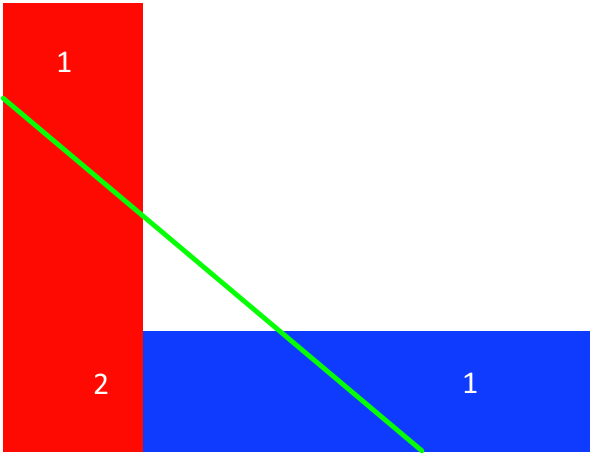
W takim przypadku chodzi o to, żeby suma pól powierzchni części oznaczonych jedynkami równało się polu powierzchni części oznaczonej dwójką.
Wisienka na torcie: istnieją co najmniej dwie metody rozwiązania tej zagadki, jedna z nich gwarantuje podział na dokładnie dwie części. Proszę podać obydwie.
Rozwiązanie zagadki tutaj.
