Prostokąt w 3d to po naszemu prostopadłościan. Tym będziemy się dziś zajmować.
Na rozgrzewkę zaczniemy jednak od "porządnych" prostokątów dwuwymiarowych.
Pytanie brzmi: czy istnieje prostokąt, którego pole powierzchni (wyrażone w jednostkach kwadratowych) jest równe długości jego obwodu (wyrażonej w jednostkach liniowych)?
Odpowiedź złośliwa brzmi: TAK.
Odpowiedź mniej złośliwa mówi, że owszem, są dwa takie prostokąty: jeden to kwadrat o boku długości 4 (4*4 = 4+4+4+4) a drugi to prostokąt o bokach długości 3 i 6 (3*6=3+3+6+6).
Proste?
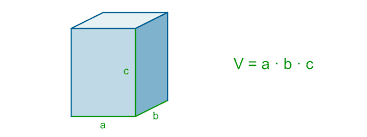
No to teraz po tej niewielkiej zakąsce przejdźmy do dania głównego: należy znaleźć wszystkie prostopadłościany, których objętość (wyrażona w jednostkach sześciennych) jest taka sama, jak ich pole powierzchni całkowitej (wyrażone w jednostkach kwadratowych).
Na zachętę przedstawię jeden taki prostopadłościan: sześcian o krawędzi 6. Jego objętość to 216 (6*6*6), tyle samo co pole powierzchni całkowitej (sześć kwadratów, każdy 6x6=36, razem 216)
Czy są inne? Jeżeli tak, to wiela ich? Jakiś konkret?
Czas - start.
brutforce 😉 mniam
3 7 42
3 8 24
3 9 18
3 10 15
3 12 12
4 5 20
4 6 12
4 8 8
5 5 10
6 6 6
Bomba!
Blisko…
Po próbach rozwiązania tego analitycznie doszedłem do czegoś takiego.
Mamy równanie
2xz+2yz+2yz =xyz
Robimy sobie wykres rozwiązań dla całej przestrzeni i otrzymujemy takie
coś
Jak widać naszym punktem przegięcia jest 6,6,6, czyli nasz przykładowy sześcian. Teraz możemy zauważyć, że zwiększając jedną z krawędzi powyżej 6 jedna z pozostałych trzech krawędzi musi być krótsza niż 6.
Teraz badamy jak jest granica przekształcenia naszego pierwszego równania:
granica
Pozwoli nam to określić jaka jest najmniejsza długość krawędzi jaką może mieć nasz prostopadłościan aby osiągnąć dane założenie. Granica ta wynosi 2 więc najmniejszą liczbą całkowitą spełniająca nasz postulat jest 3. Zawęziliśmy sobie więc długość jednej z krawędzi do wartości {3,4,5,6}.Dodatkowo jeżeli jedna z krawędzi jest mniejsza niż 6 to jedna musi być większa od 6 aby spełnione było nasze pierwsze równanie. Dla cyfry 6 mamy już rozwiązanie w postaci trójki liczb 6,6,6, następnie sprawdzamy co otrzymamy dla krawędzi równej 5.
5yz=10y+10z+2yz
3yz=10y+10z
3yz-10y=10z
y(3z-10)=10z
y=10z/(3z-10)
Analizujemy teraz dla z=5 otrzymujemy:
y=50/(15-10)=10 Czyli otrzymujemy trójke (5,5,10)
Następnie z = 4
y=40/(20-10)=4 Jak widać trzecia krawędź jest mniejsza od 6 więc dalsze sprawdzanie dla z<4 nie ma sensu. Dodatkowo możemy zbadać funkcje y=10z/(3z-10) różniczkując ją po zmiennej z. Otrzymujemy coś takiego
monotoniczność
Jak widać badanie funkcji poniżej 4 nie ma sensu gdyż funkcja jest malejąca. Badamy dalej dla z=10 (najbliższa liczba która da nam wynik w postaci liczby całkowitej) pamiętając że wraz ze wzrostem z wartości funkcji rosną.
y=100/(30-10)=5
Analogicznie trzecia krawędź jest mniejsza od 6 więc przestajemy sprawdzać.
Dla pozostałych wartości x postępujemy podobnie. Ufff……
No i to się nazywa podejście z głową. Doskonale!