Rozwiązanie mocno średniej zagadki

https://xpil.eu/75ms

Pierwsza część zagadki wydaje się być do ogarnięcia za pomocą komputera, jednak próby napisania w Pythonie algorytmu podziału zbioru na podzbiory pochłonęły mi zaskakująco dużo czasu. W końcu poddałem się i wziąłem gotowca z tej strony, minimalnie tylko przerabiając go na potrzeby zagadki.

import copy


def podział(zbiór):

    def podział_rek(zbiór, indeks, ret):
        if indeks == len(zbiór):
            yield ret
            return

        for i in range(len(ret)):
            ret[i].append(zbiór[indeks])
            yield from podział_rek(zbiór, indeks + 1, ret)
            ret[i].pop()

        ret.append([zbiór[indeks]])
        yield from podział_rek(zbiór, indeks + 1, ret)
        ret.pop()

    ret = []
    yield from podział_rek(zbiór, 0, ret)


def znajdź_optymalne_podziały(N):
    zbiór = list(range(1, N+1))
    średnia_całości = sum(zbiór)/len(zbiór)
    maksymalne_odchylenie = 0
    optymalne_podziały = []

    for p in podział(zbiór):
        średnia_średnich = sum(sum(zbiór)/len(zbiór) for zbiór in p) / len(p)
        odchylenie = abs(średnia_średnich - średnia_całości)

        if odchylenie > maksymalne_odchylenie:
            maksymalne_odchylenie = odchylenie
            optymalne_podziały = [copy.deepcopy(p)]
        elif odchylenie == maksymalne_odchylenie:
            optymalne_podziały.append(copy.deepcopy(p))

    return optymalne_podziały, maksymalne_odchylenie


def main():
    N = 12
    optymalne_podziały, maksymalne_odchylenie = znajdź_optymalne_podziały(N)
    print("Optymalne podziały:")
    for podział in optymalne_podziały:
        print("  ", podział)
    print("Maksymalne odchylenie: ", maksymalne_odchylenie)


if __name__ == '__main__':
    main()

Wynik:

Optymalne podziały:
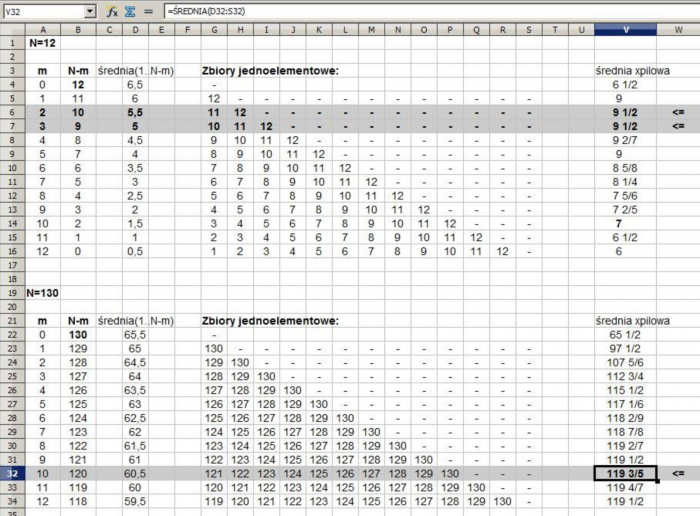
   [[1, 2, 3, 4, 5, 6, 7, 8, 9, 10], [11], [12]]
   [[1, 2, 3, 4, 5, 6, 7, 8, 9], [10], [11], [12]]
   [[1], [2], [3, 4, 5, 6, 7, 8, 9, 10, 11, 12]]
   [[1], [2], [3], [4, 5, 6, 7, 8, 9, 10, 11, 12]]
Maksymalne odchylenie:  3.0

Jeżeli chodzi o drugą część zagadki, czyli rozwiązanie ogólne dla dowolnego N, to robi się ciekawie.

Trzeba najpierw zauważyć kilka spraw:

Po pierwsze, jeżeli z optymalnego rozwiązania weźmiemy dwa podzbiory, nazwijmy je S1 i S2, ze średnimi w każdym podzbiorze odpowiednio A1 i A2, takimi, że A1 < A2, to jest gwarantowane, że każda liczba w S1 jest mniejsza od każdej liczby w S2. Gdyby bowiem było inaczej, czyli gdyby w S1 była liczba X większa od liczby Y w S2, to dałoby się poprawić wynik zamieniając X i Y miejscami.

Po drugie zaś, jeżeli mamy dwa podzbiory S1 i S2 (w każdym co najmniej dwie liczby) ze średnimi A1<A2, to jeżeli weźmiemy największą liczbę z pierwszego podzbioru i przełożymy ją do drugiego, w efekcie obydwie średnie się zmniejszą. Jest to gwarantowane, bo z S1 zabraliśmy największą liczbę (a więc A1 się zmniejszyła), a do S2 dodaliśmy liczbę, która jest mniejsza od wszystkich liczb, które tam były (zgodnie z akapitem powyżej), więc A2 też się zmniejszyła. Tym samym średnia średnich na pewno oddaliła się od średniej z całego zbioru liczb {1..N}.

Jeżeli więc podzielimy nasz początkowy zbiór {1..N} na K podzbiorów, a następnie zaczniemy przekładać największą liczbę z podzbioru o najmniejszej średniej do tego następnego, i będziemy kontynuować tę czynność dla wszystkich podzbiorów, gdzie jest to możliwe, za każdym razem poprawiając wynik (czyli oddalając się ze średnią średnich od średniej całości), to w efekcie dostaniemy podział w postaci:

{{1},{2},...{K-1},{K, K+1, ..., N}}

Innymi słowy optymalny podział dla K podzbiorów to taki, gdzie pierwsze K-1 podzbiorów zawierają po jednym elemencie (odpowiednio od 1 do K-1), a ostatni "duży" podzbiór - wszystkie pozostałe elementy od K do N.

Notka: ponieważ zagadka jest symetryczna, można też na odwyrtkę, czyli jeden "duży" podzbiór {1, 2, ... , N-K} plus pojedyncze "podzbiorki" {N-K+1},{N-K+2},...,{N} - przykład dla N=12 widać w rozwiązaniu pierwszej części zagadki.

Pozostaje jedynie kwestia tego jak znaleźć optymalne K. Wiemy (z pierwszej części zagadki), że dla N=12 K=3 lub K=4, ale nic poza tym.

Spróbujmy ugryźć drania arytmetycznie.

Wiemy, że suma średnich dla podzbiorów {1},...{K-1} wynosi:

\[\frac{K(K-1)}{2}\]

Wiemy też, że średnia w ostatnim ("dużym") podzbiorze {K..N} wynosi:

\[\frac{K+N}{2}\]

Składając to do kupy, po paru prostych przekształceniach okazuje się, że średnia średnich dla wszystkich podzbiorów to:

\[\frac{(K+\frac{N}{K})}{2}\]

Chcemy teraz znaleźć ekstremum tej średniej średnich.

Notka: formalnie chcemy tak naprawdę znaleźć maksimum różnicy między średnią początkową a średnią średnich, ale ponieważ średnia początkowa jest stała i niezależna od K, nie będziemy sobie niepotrzebnie komplikować obliczeń.

Pochodna tego wyrażenia po K to:

\[\frac{1}{2} (1-\frac{N}{(K^2)})\]

Jak niektórzy być może jeszcze pamiętają ze szkoły średniej, funkcja osiąga ekstremum w punkcie, w którym jej pierwsza pochodna jest równa zeru. Aby powyższe wyrażenie wyszło na zero, musi zachodzić:

\[N=K^2\]

czyli

\[K=\sqrt{N}\]

(pamiętamy, że zarówno N jak i K są dodatnie, więc nie ma tu ryzyka minusów pod pierwiastkiem)

Tak naprawdę ponieważ K jest naturalne, musimy ów pierwiastek zaokrąglić, i czasem będzie działać tylko zaokrąglenie w górę, czasem tylko w dół, a czasem i jedno i drugie (stąd dla N=12 mamy K=3 albo K=4 jak widać w rozwiązaniu pierwszej części):

Tym samym odpowiedź na drugą część zagadki brzmi: zbiór {1..N} należy podzielić na podzbiory {1}, {2}, ... ,{K-1}, {K, .., N}, a K przyjąć w okolicach \( \sqrt{N}\).

A jak Wam poszło?

1Pierwszy odezwał się Waldek, który rozwiązał pierwszą część zagadki śpiewająco, a drugą wręcz operetkowo. Waldek rozwodzi się dość szczegółowo (i pomysłowo) nad podziałami zbiorów i nawet rozwiązuje problem tego nieszczęsnego zaokrąglenia pierwiastka (czy w górę, czy w dół, czy wsioryba). Co prawda nie widzę tam nigdzie samego pierwiastka, ale obstawiam, że gdyby się wgryźć, to by się znalazł. W każdym razie obliczenia się zgadzają. Czapki z głów.

2Jako drugi z zagadką zmierzył się Rozie, który jednakowoż poległ srodze.

3Kolejnym rozwiązującym był Cichy Fragles, którego rozumowanie i matematyka są podobne do Waldkowych - zaliczam.

4Rzutem na taśmę, we środę o piątej nad ranem poprawne rozwiązanie nadesłał Krzysiek, ostatni rozwiązujący. Krótko, prawidłowo:

https://xpil.eu/75ms