Dla przypomnienia: spośród 70 liczb całkowitych od 1 do 70 piątka przyjaciół wybrała po pięć liczb w taki sposób, że:
- Nie ma tam żadnych liczb pierwszych
- Każda liczba ma co najmniej dwa różne podzielniki pierwsze
- Iloczyn każdej piątki jest taki sam.
Pytanie: ile wynosi ów iloczyn?
Zaczniemy od tego, że ponieważ w każdej piątce iloczyn liczb jest ten sam, to znaczy że u każdego z przyjaciół iloczyn rozkłada się na te same czynniki pierwsze.
Spróbujmy zbudować mniejszy przykład na zobrazowanie tej oczywistości:
Weźmy dwie grupy po dwie liczby:
Grupa 1: (24,75)
Grupa druga: (20, 90)
W obu grupach iloczyn wynosi 1800.
Rozkład 1800 na czynniki pierwsze to 2*2*2*3*3*5*5
24 = 2*2*2*3, 75 = 3*5*5 (czyli wszystkie czynniki pierwsze to 2*2*2*3*3*5*5)
20=2*2*5, 90=2*3*3*5 (znów te same czynniki pierwsze: 2*2*2*3*3*5*5)
Nie ma cudów: w każdej piątce mamy ten sam zestaw czynników pierwszych, są one inaczej rozdystrybuowane między poszczególne liczby, ale razem do kupy są identyczne.
No dobra. Wiemy już, że każda grupa ma ten sam zestaw czynników pierwszych. Przyjrzyjmy się jeszcze raz przykładowi powyżej: Jeżeli przemnożymy przez siebie wszystkie liczby ze wszystkich grup (czyli 24*75*20*90), dostaniemy 3240000, liczba której rozkład na czynniki pierwsze to 2*2*2*3*3*5*5 * 2*2*2*3*3*5*5.
Z powyższego widać, że zarówno dwójki jak i trójki czy piątki muszą się pojawiać w tym "dużym" iloczynie parzystą ilość razy. Mamy sześć dwójek i po cztery trójki i piątki. Czy to przypadek?
Nie! Ponieważ mamy dwie grupy, a w każdej identyczny zestaw podzielników pierwszych, to logiczne jest, że każdy z podzielników wystąpi (w całym dużym zestawie) parzystą ilość razy. Gdyby któryś z czynników występował trzy razy, wówczas nie dałoby się tej trójki rozłożyć równomiernie pomiędzy dwie grupy.
Analogicznie jeżeli mamy pięć grup, to po przemnożeniu wszystkich 25 liczb każdy czynnik pierwszy iloczynu musi wystąpić 5 albo 10 albo 15 razy itd. Ilość wystąpień każdego z czynników pierwszych musi się dzielić przez pięć.
Weźmy się teraz za samo gęste, czyli zobaczmy te nasze nieszczęsne liczby:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70
Na dzień dobry możemy wywalić wszystkie liczby pierwsze (bo nie mają co najmniej dwóch różnych podzielników pierwszych ) oraz ich całkowite potęgi (z tego samego powodu). Zostaje nam lista z 41 liczbami:
6, 10, 12, 14, 15, 18, 20, 21, 22, 24, 26, 28, 30, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 65, 66, 68, 69, 70
Co dalej?
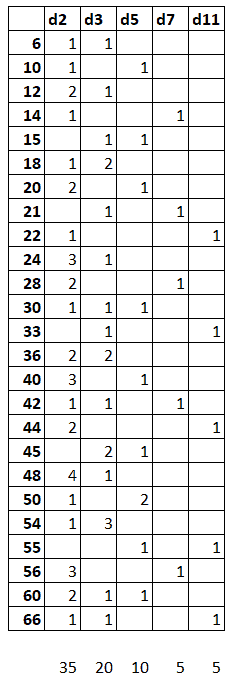
Zobaczmy jak wyglądają podzielniki poszczególnych liczb na naszej liście. W tym celu zapiszemy sobie naszych 41 liczb w pionowym słupku, a w kolumnach obok dodamy ile razy każda z nich dzieli się przez kolejne liczby pierwsze:

Jak wyjaśniłem wcześniej, każdy z podzielników musi wystąpić co najmniej pięć razy. Przez 13 dzielą się jednak tylko 4 liczby z naszej listy - to za mało, żeby "obdarować" nimi po równo pięć osób. Usuwamy więc 26, 39, 52 i 65. Podobnie sprawa ma się z wielokrotnościami 17, 23, 29 i 31, a więc usuwamy też 34, 38, 46, 51, 57, 58, 62, 68 i 69.
Co nam pozostało?
Zostało nam 28 liczb:

Wśród nich jest 25 liczb, które wybrali bohaterowie naszej zagadki, a więc trzy liczby trzeba odrzucić.
Jak ustalić te trzy?
Zaczniemy od policzenia wszystkich czynników pierwszych (a więc sumujemy kolumny d2, d3, d5 itd aż do d11):
d2: 36
d3: 22
d5: 12
d7: 8
d11: 5
Uwagę przykuwa kolumna d7, czyli liczby podzielne przez 7. Siódemka występuje wśród podzielników 8 razy, a więc o trzy razy za dużo. Trzeba więc usunąć trzy liczby podzielne przez siedem i to w taki sposób, żeby jednocześnie zmniejszyć ilość piątek o 2 (do 10), trójek do 20 a dwójek do 35.
Tylko dwie z tych 28 liczb liczb dzielą się jednocześnie przez 5 i przez 7, a więc 35 i 70 są oczywistymi kandydatami do usunięcia: dzięki temu dostaniemy 10 piątek.
Usuwając 70 zmniejszamy też liczbę dwójek o jeden - zostaje 35:

OK, pozostała nam do usunięcia jeszcze jedna liczba z 26 powyżej i wiemy na pewno, że jest to jedna z podzielnych przez 7. Wiemy też, że mamy już 25 dwójek, więc nie możemy usunąć liczby parzystej. No i mamy 22 trójki, a potrzebujemy 20. Czyli jedyna opcja to 63. Po usunięciu 63 z listy pozostaje nam 25 liczb:
Każdy dostanie po siedem dwójek, cztery trójki, dwie piątki i po jednej siódemce i jedenastce. W każdej grupie iloczyn wyniesie więc:
\(2^7*3^4*5^2*7*11=19 958 400\)I to w zasadzie powinno być na tyle, chociaż czuć pewien niedosyt, prawda? No bo niby zagadka rozwiązana, ale chciałoby się zobaczyć chociaż jeden przykład jak te liczby są właściwie porozkładane między piątką przyjaciół.
Proszę bardzo:
{6, 15, 56, 60, 66}, {10, 14, 48, 54, 55}, {12, 18, 42, 44, 50}, {20, 21, 33, 36, 40}, {22, 24, 28, 30, 45}
A na ile różnych sposobów da się te liczby wybrać?
Jak już nadmieniłem, wszystkich kombinacji 25 liczb spośród 70 jest coś ponad 4 kwintyliardy, czyli strasznie dużo.
Sposobów na rozparcelowanie naszych 25 pracowicie znalezionych liczb między pięć osób tak, żeby spełnić warunki zagadki jest ciut ponad 17000 (nie będę ich tutaj podawał).
Jeżeli natomiast uwzględnimy powtórzenia, a więc potraktujemy wariant kiedy Alicja ma, dajmy na to, {6, 15, 56, 60, 66} a Bernard - {10, 14, 48, 54, 55} a potem na odwrót jako dwa różne układy, wówczas trzeba jeszcze przemnożyć te 17000 przez 5!, co daje nam pozornie duże okolice półtora miliona. Jednak w porównaniu do czterech kwintyliardów to w dalszym ciągu w zasadzie zero.
Wniosek?
Oni tych liczb nie wylosowali. Specjalnie tak zakombinowali, żeby wyszło.
Bo oni zawsze coś kombinują, ci cholerni matematycy. W ogóle nie można im ufać 😉
To ja zaproponuję coś łatwiejszego. I potrzeba tylko trzech przyjaciół:
Trzej przyjaciele wybrali się do pizzerii (ja znów o jedzeniu). Wybrali pizzę za 30zł, więc złożyli się po 10 zł. Kelner przyjął zamówienie, a potem zorientował się, że dziś na tę pizzę jest promocja i kosztuje 25 zł. Oddał więc przyjaciołom po złotówce, a dwa złote zostawił sobie jako napiwek (łobuz!). Teraz policzmy: zwrócił im po 1zł, to tak, jakby złożyli się po 9zł. Trzy razy dziewięć to 27 i 2zł u kelnera to razem 29. Więc gdzie jest jeszcze złotówka?
(może nie powinienem tego opowiadać informatykom, również księgowi nie dają się nabrać).
Jeżeli pizza kosztuje 25zł to powinni byli się zrzucić każdy po 8zł 33gr. Zrzucili się po 10zł, czyli każdy dał o 1zł 67gr za dużo. Potem każdy dostał złotówkę z powrotem od kelnera, a pozostałe 67gr przemnożone przez 3 daje 2zł napiwku. Wszystko się zgadza.
Wiedziałem, że informatykom nie warto tego opowiadać. Nie ma efektu zaskoczenia…
Ba, ale i tak na pierwszy rzut oka wydaje się nieprawdopodobne, że można tych 25 liczb podzielić między przyjaciół aż na ponad 17 tys. sposobów, mimo że to ułamek ułamka tych 4 kwintyliardów. Ale wygląda to już znacznie prawdopodobniej, gdy weźmie się pod uwagę, jak specyficzną selekcję przeszły te liczby na tym etapie:)