Pierwsza część zagadki jest na tyle prosta, że można ją rozwiązać za pomocą kartki A4, linijki, cyrkla i ołówka. Ja jestem na tyle leniwy, że - jakże by inaczej - napisałem sobie w Pythonie funkcję, która dla zadanego koła rysuje owo koło oraz dwie styczne doń, przechodzące przez (0,0). Dzięki temu mogłem sobie wirtualnie kombinować z różnymi ustawieniami drzew.
Zanim jednak do tego doszło, musiałem zabazgrać całkiem sporo kartek próbując ustalić równanie tych stycznych. Zagadnienie jest na poziomie szkoły średniej, trzeba znać równanie prostej, równanie okręgu oraz policzyć deltę trójmianu kwadratowego i pamiętać, że trójmian ów ma dokładnie jedno miejsce zerowe wtedy i tylko wtedy, jeżeli delta jest równa zero.
To z kolei daje nadzieję tym, którzy siedząc dziś w szkolnej ławce zastanawiają się po kiego czorta liczyć tę cholerną deltę, przecież to się, kwajegomać, nigdy do niczego nie przyda. Otóż, jak widać, przyda się. Do szukania rozwiązań głupich zagadek na niszowych blogach 🙂
Zaczynamy zatem od początku, czyli od równania prostej: \(y=ax+b\). Ponieważ jednak nasze oko siedzi w punkcie (0,0), możemy odrzucić b i zostaje samo: \(y=ax\).
Drugi element układanki to koło o środku w punkcie \((x_1, y_1)\) oraz promieniu r. Równanie opisujące takie koło w układzie współrzędnych to: \((x-x_1)^2+(y-y_1)^2=r^2\).
Aby owa prosta i koło miały w ogóle jakieś wspólne punkty, ich wykresy muszą się gdzieś spotykać, czyli mieć jakiegoś wspólnego iksa i igreka (jednego lub dwa, bo linia może przeciąć okrąg lub być doń styczna). Mamy więc do rozwiązania układ równań:
$$\begin{cases}y=ax\\(x-x_1)^2+(y-y_1)^2=r^2\\ \end{cases}$$
Nie chce mi się teraz przepisywać wszystkich kroków pośrednich, bo nie jestem aż tak zajadły - podpowiem tylko, że najpierw podstawiamy w drugim równaniu y z równania pierwszego, potem rozwiązujemy je dla x, a potem przekształcamy tak, żeby po lewej stronie mieć samo a (ale nie Samoa, tam jest spacja). Okaże się, że wyrażenie na a (czyli współczynnik nachylenia stycznej) jest samo w sobie trójmianem kwadratowym, którego delta musi być równa zero (bo tylko wtedy prosta będzie miała dokładnie jeden wspólny punkt z okręgiem, czyli będzie doń styczna). Okazuje się, że są dwa takie rozwiązania:
$$a_1=\frac{-(x_1 x_2)-\sqrt{-r^4+r^2x_1^2+r^2x_2^2}}{(r^2-x_1^2)}$$
$$a_2=\frac{-(x_1 x_2)+\sqrt{-r^4+r^2x_1^2+r^2x_2^2}}{(r^2-x_1^2)}$$
Znając współczynniki \(a_1, a_2\) możemy w końcu przystąpić do samego gęstego, czyli napisania sobie kodu w Pythonie, który nam takie kółko narysuje, wraz z dwiema doń stycznymi. A ponieważ wiemy, że będziemy potrzebowali narysować takich kółek więcej niż jedno, napiszemy sobie funkcję, która rysuje wszystkie kółka na raz, a nie tylko pojedyncze:
import numpy as np
import matplotlib.pyplot as plt
def rysuj_kółka_i_styczne(kółka):
# liczymy odległości kółek od punktu (0,0)
odległości = [np.sqrt(x**2 + y**2) for x, y, _ in kółka]
for (x1, x2, r), odległość in zip(kółka, odległości):
kółko = plt.Circle((x1, x2), r, color='b', fill=False)
# rysujemy kółko
plt.gca().add_patch(kółko)
# wpisujemy przybliżoną odległość (do drugiej części zagadki)
plt.text(x1, x2, f"{odległość:.2f}", ha='center', va='center', fontsize=5)
# Liczymy współczynniki nachylenia a1 i a2
a1 = (-(x1 * x2) - np.sqrt(-r**4 + r**2 *
x1**2 + r**2 * x2**2)) / (r**2 - x1**2)
a2 = (-(x1 * x2) + np.sqrt(-r**4 + r**2 *
x1**2 + r**2 * x2**2)) / (r**2 - x1**2)
# Ustalamy początkowe i końcowe wartości iksów dla naszych linii
x_values = [-1.0, 4.0]
plt.plot(x_values, a1*np.array(x_values), '-r', linewidth=0.5)
plt.plot(x_values, a2*np.array(x_values), '-g', linewidth=0.5)
# upewniamy się, że wykres jest tej samej wielkości w każdy poprzek
# (żeby kółka były okrągłe a nie elipsoidalne)
plt.gca().set_aspect('equal', adjustable='box')
# ustalamy zakresy osi x i y
plt.xlim(-1, 4)
plt.ylim(-1, 4)
# rysujemy siatkę współrzędnych
plt.xticks(np.arange(-1, 4, 1))
plt.yticks(np.arange(-1, 4, 1))
plt.grid(True, color='#E0E0E0', linewidth=0.5)
# Wyświetlamy całość
plt.show()
if __name__ == '__main__':
r = 0.25
kółka = [(0,1,r), (1,1,r),(1,0,r), (1,2,r), (2,1,r), (1,3,r), (2,3,r), (3,2,r), (3,1,r)]
rysuj_kółka_i_styczne(kółka)
Powyższy kod wyprodukuje nam:
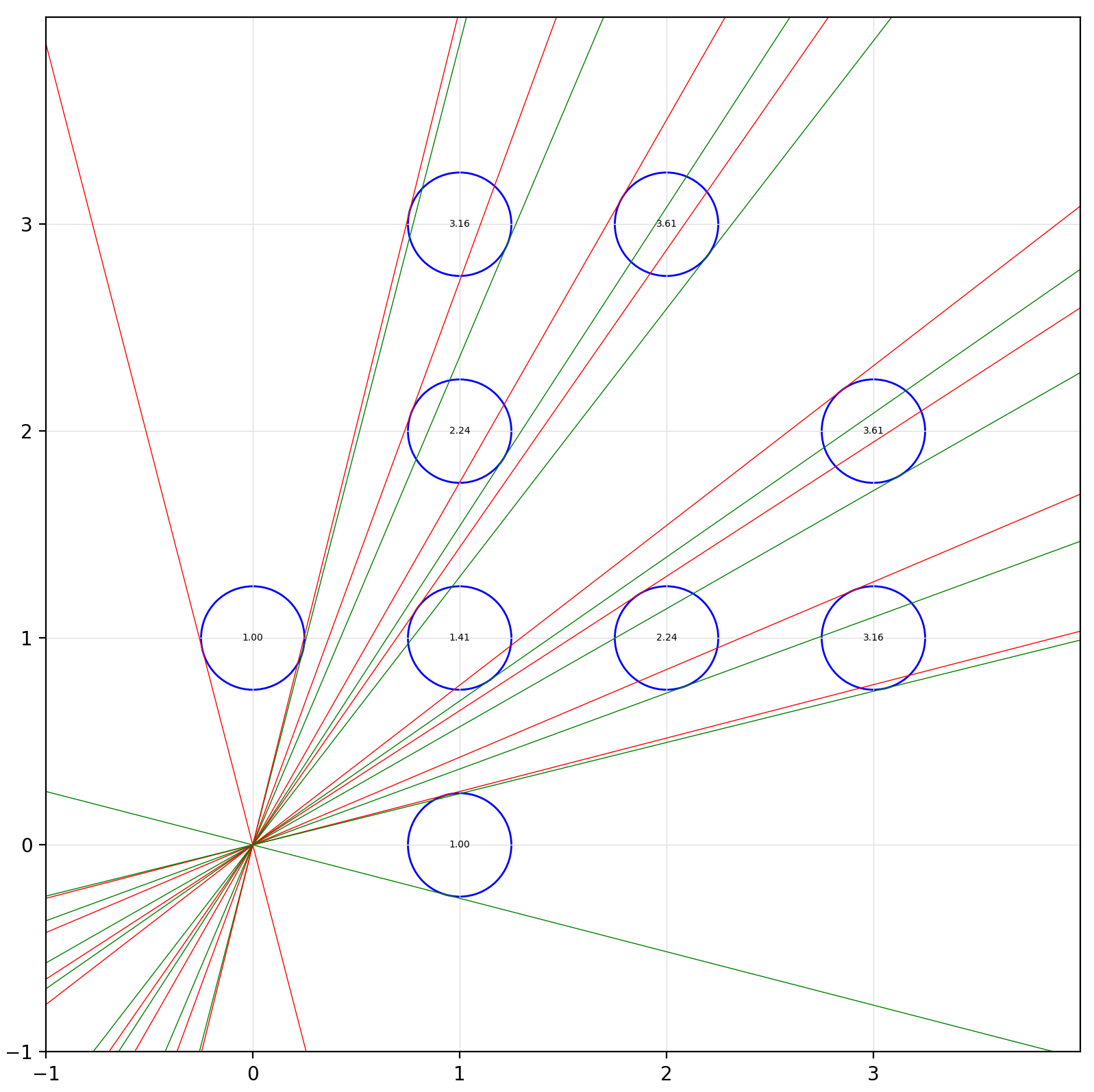
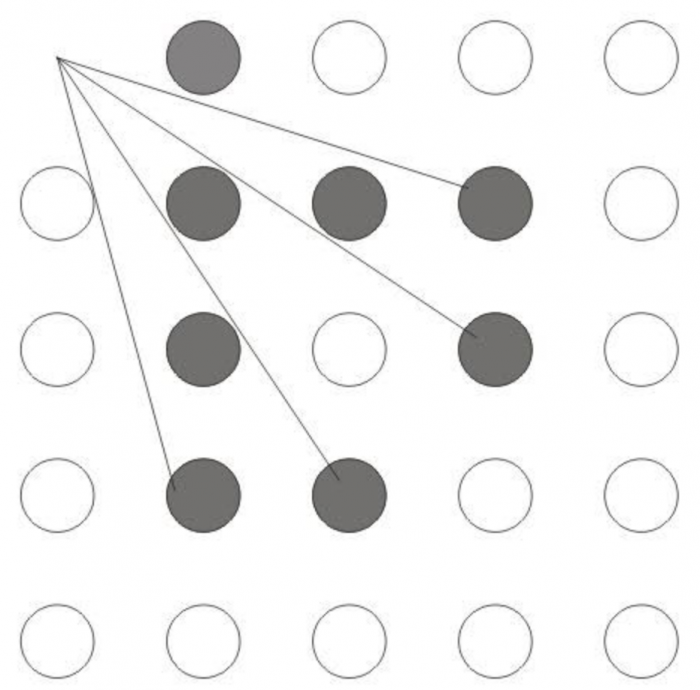
Oczywiście zamiast patrzeć dookoła, skupiłem się tylko na pierwszej ćwiartce układu, bo wiadomo, symetria. Widać siedem kółek o współrzędnych dodatnich oraz dwa leżące na osiach. Rozciągając to na pozostałe trzy ćwiartki widać, że łącznie widać będzie 32 drzewa i to jest prawidłowa odpowiedź do pierwszej części zagadki.
Jeżeli natomiast chodzi o część drugą, to mając już narzędzie w postaci powyższej funkcji należało tylko pracowicie poukładać kółka o promieniu 0.1 w taki sposób, żeby zasłaniały wszystko dalsze, a następnie wybrać to z maksymalną odległością. Po paru minutach kombinowania udało mi się uzyskać następujący efekt:
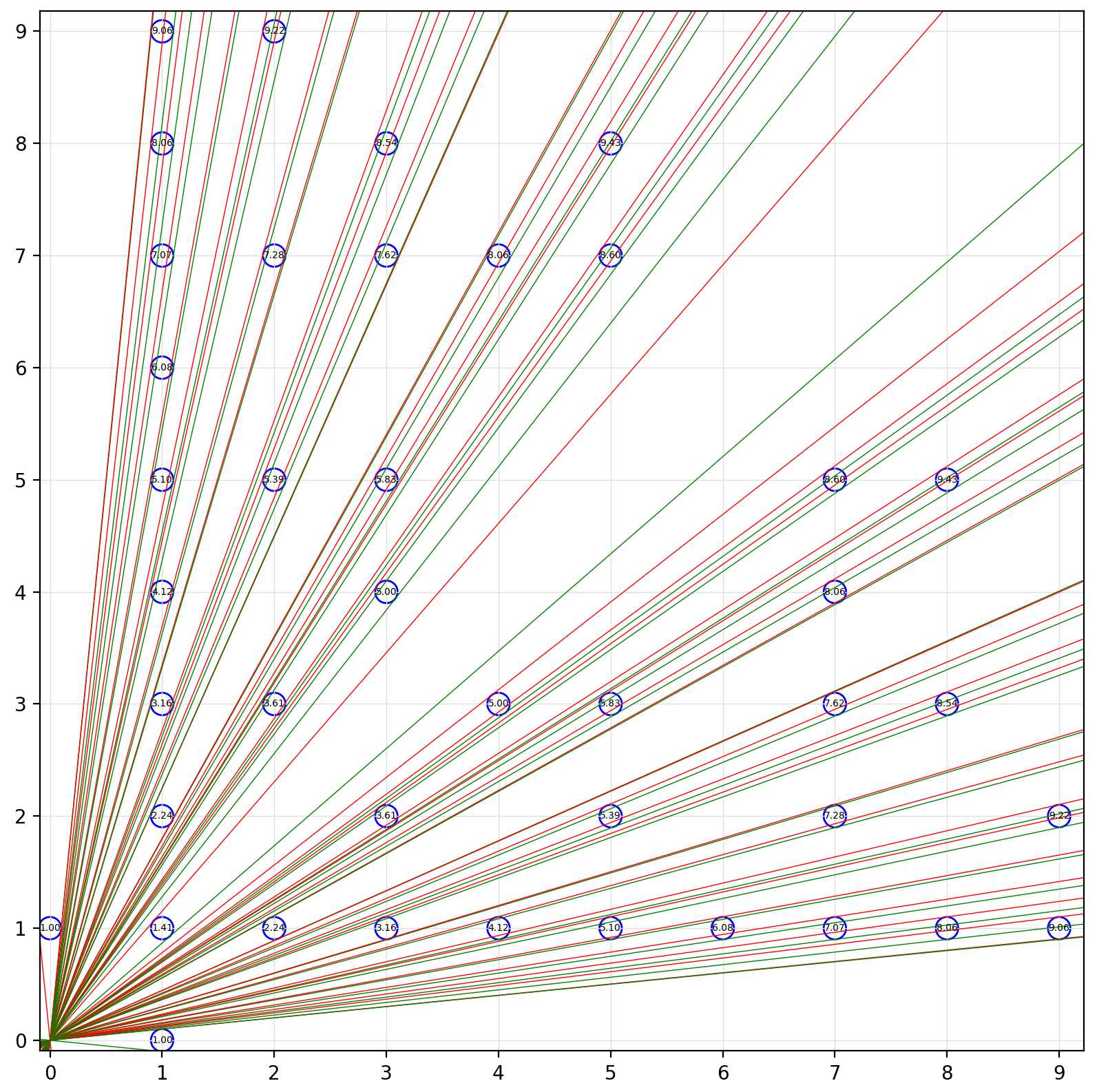
Dla zainteresowanych, kółka do powyższego wykresu uzyskałem tak:
kółka = [(0, 1, r),
(1, 0, r), (1, 1, r), (1, 2, r), (1, 3, r), (1, 4, r), (1,5, r), (1, 6, r), (1, 7, r), (1, 8, r), (1, 9, r),
(2, 1, r), (2, 3, r), (2, 5, r), (2, 7, r), (2, 9, r),
(3, 1, r), (3, 2, r), (3, 4, r), (3, 5, r), (3, 7, r), (3, 8, r),
(4, 1, r), (4, 3, r), (4, 7, r),
(5, 1, r), (5, 2, r), (5, 3, r), (5, 7, r), (5, 8, r),
(6, 1, r),
(7, 1, r), (7, 2, r), (7, 3, r), (7, 4, r), (7, 5, r),
(8, 1, r), (8, 3, r), (8, 5, r),
(9, 1, r), (9, 2, r)
]
Na pierwszy rzut oka wydaje się, że rozwiązanie to 9.33 metrów (drzewo (5,8)). Jednak po uważniejszym przyjrzeniu się zauważamy co dzieje się między drzewami (2,1) oraz (7,3) - otóż okazuje się, że nie pokrywają one całego kąta i między nimi jest maleńka szczelina, przez którą widać drzewo (9,4). Widać co prawda bardzo wąski pasek tego drzewa - ale jednak widać. Żeby nie było wątpliwości, oto zbliżenie na punkt (9,4):
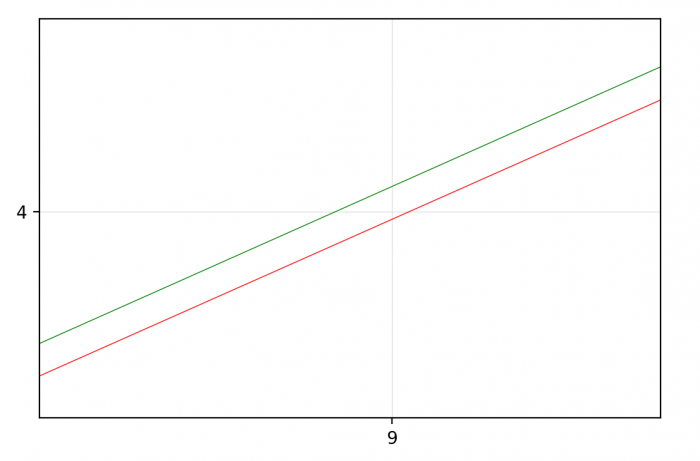
Ostatecznie więc: $$\sqrt{9^2+4^2}-0.1\approx 9.75 $$ i to jest poprawna odpowiedź.
Oczywiście można by się pokusić o jeszcze dokładniejsze rozwiązanie - przecież skoro linie czerwona i zielona na powiększeniu powyżej nie leżą symetrycznie względem punktu (9,4), to wynik jest odrobinę przekłamany. Dlatego właśnie dodałem, że uznam rozwiązanie z dokładnością do dwóch miejsc po przecinku, bo błąd jest rzędu 10-3, czyli dla zadanej dokładności - pomijalny.
A jak Wam poszło?
Z zagadką zmierzył się tylko jeden Czytelnik, za to aż dwa razy 🙂
1Pierwszy odezwał się Waldek, który rozwiązał poprawnie drugą część zagadki, natomiast całkiem zawalił - pierwszą, tę łatwiejszą. Nie zaliczam.

2Jako drugi, dla odmiany, odezwał się również Waldek - tym razem obydwa rozwiązania poprawne. Bonusik - Waldek wysyłał odpowiedź podczas nagłego ataku weny Tfurczej, więc poza matematyką mamy też odrobinę poezji, z której wnioskuję, że poprzednia odpowiedź na pierwszą część zagadki była prawidłowa przy założeniu, że 0.25 to średnica drzewa a nie promień.

Jeżeli chcesz do komentarza wstawić kod, użyj składni:
[code]
tutaj wstaw swój kod
[/code]
Jeżeli zrobisz literówkę lub zmienisz zdanie, możesz edytować komentarz po jego zatwierdzeniu.