Tym razem w zagadce należało wykazać, że na płaszczyźnie, której każdy punkt jest w jednym z trzech kolorów, istnieje nieskończenie wiele par punktów tego samego koloru, odległych od siebie o 1.
Większość ludzi próbujących rozwiązać tę zagadkę dochodzi w pewnym momencie do sześciokąta foremnego zbudowanego z trójkątów równobocznych o wspólnym wierzchołku - ale sześciokąt ów nijak nie przybliża nas do rozwiązania.
Zamiast tego należy dwa trójkąty równoboczne (o boku 1 i wierzchołkach w trzech różnych kolorach) skleić w romb. Romb ów ma dwa kąty ostre i dwa rozwarte, a jak się człowiek przez moment skupi to zauważy, że aby zachować warunki zadania, wierzchołki przy kątach ostrych muszą być tego samego koloru. Czynność powtarzamy - i powstałe w ten sposób dwa romby łączymy ze sobą wierzchołkami (przy kącie ostrym), a następnie obracamy jeden z nich wokół wierzchołka tak, aby przeciwległe wierzchołki (również przy kątach ostrych) były od siebie odległe dokładnie o 1. Skoro wierzchołki te są tego samego koloru, to widać, że dwa punkty tego samego koloru muszą być odległe o 1.
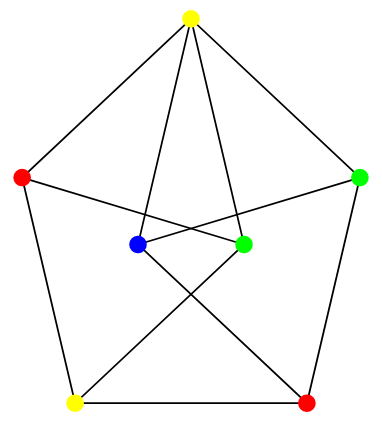
Figura ta nazywa się wrzecionem Mosera (https://mathworld.wolfram.com/MoserSpindle.html).
Poniżej obrazek zachachmęcony ze strony Wolfram Alpha, pokazujący pokolorowanie wrzeciona Mosera czterema kolorami (każdy odcinek na tym obrazku ma długość 1):
Zadanie można próbować rozszerzyć na kolejne, coraz większe liczby kolorów. Okazuje się, że o ile dla trzech kolorów zadanie jest jeszcze w miarę proste (wrzeciono Mosera powyżej), o tyle dla czterech kolorów minimalny znany obecnie zestaw punktów wymaganych do rozwiązania zadania, zwany grafem deGrey-a, składa się już z 1581 punktów:
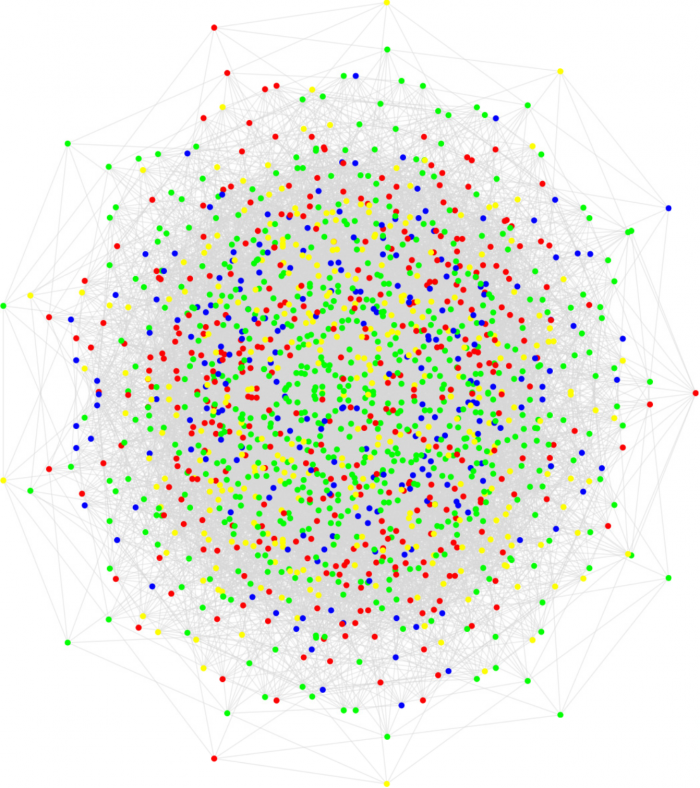
Errata: najmniejszy znany obecnie graf wymagający co najmniej pięciu kolorów ma 826 wierzchołków.
A co z pięcioma kolorami?
Okazuje się, że nie wiadomo. Udało się udowodnić brak rozwiązania dla ośmiu i więcej kolorów (innymi słowy jeżeli różnych kolorów jest co najmniej osiem, to da się pokolorować płaszczyznę tak, żeby żadne dwa punkty odległe o 1 nie były tego samego koloru), natomiast nie wiemy jak sprawa wygląda dla 5, 6 i 7 kolorów. Jest to jeden z nierozwiązanych do dziś problemów, znany pod nazwą problemu Hadwigera-Nelsona (https://mathworld.wolfram.com/Hadwiger-NelsonProblem.html).
Zagadnienie można też rozciągnąć na wyższe wymiary. Na przykład w przestrzeni 3d udało się udowodnić możliwość nieistnienia takiej pary dla liczby kolorów równej 16 lub więcej, natomiast nie wiadomo jak to wygląda dla 6-15 kolorów (przy pięciu kolorach udowodniono, że taka para zawsze istnieje).
Dla przestrzeni n-wymiarowej łatwo znaleźć maksymalną liczbę kolorów, dla której na pewno nie ma rozwiązania; wynosi ona n+2, a szczegółową rozpiskę i wytłumaczenie można znaleźć tutaj (w skrócie: budujemy odpowiedniki wrzeciona Mosera w wyższych wymiarach). Natomiast z górną granicą jest już gorzej...
A jak Wam poszło?
Chyba po raz pierwszy mamy sytuację, że jeden Czytelnik nadesłał więcej odpowiedzi, niż wszyscy pozostali razem wzięci 🙂
1Na dzień dobry rękawicę podjął Waldek. Strzelił w ciemno. Spudłował. Nie zaliczam.

2Niecałe trzy godziny później odezwał się Cichy Fragles - i pozamiatał. Zaliczam.

3Jakiś czas później Waldek poszedł po rozum do głowy i skorygował swoją pierwotną odpowiedź:
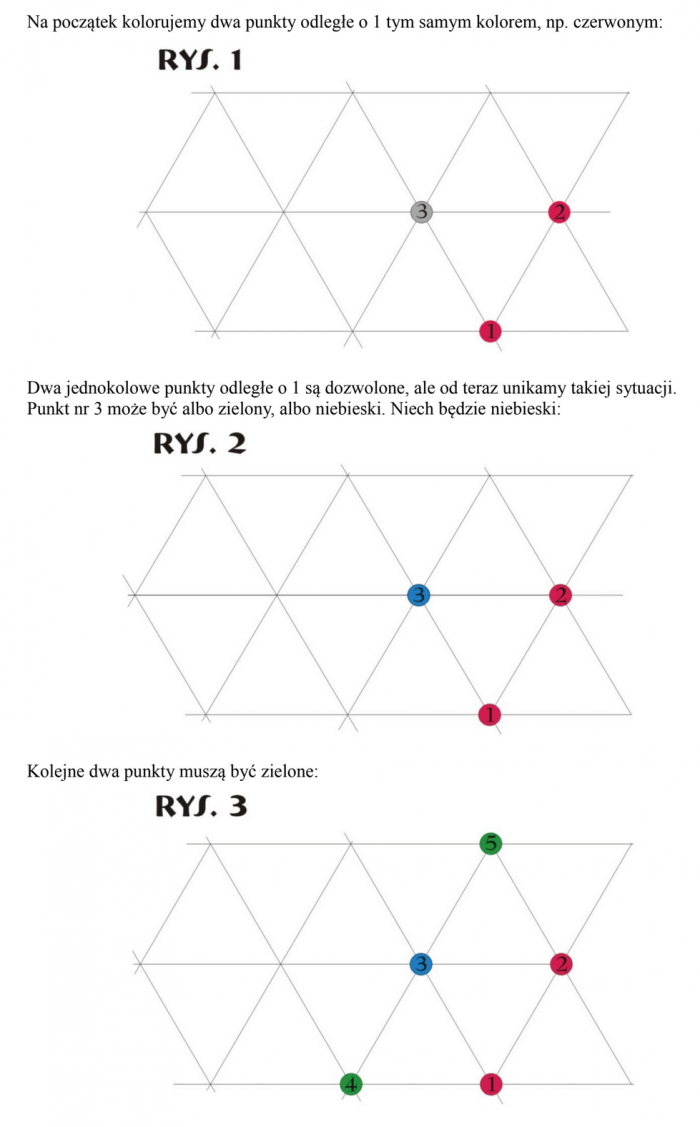

Rozwiązanie całkiem eleganckie, logiczne i estetyczne, tylko że do jakiejś zupełnie innej zagadki. Dlaczego w pierwszym kroku startujemy od dwóch punktów pokolorowanych tak samo? Nie zaliczam.
Nota bene nawet jeżeli dotarlibyśmy do sytuacji podobnej jak na rysunku 5, tylko z punktami 2 i 5 zamienionymi miejscami, a następnie punkt 7 pomalowali na zielono, nadal nie uzyskalibyśmy odpowiedzi na oryginalne pytanie, o czym zresztą wspominam w treści tego wpisu, a na co również wpadł Rzast w odpowiedzi numer 5.
Minęło trochę strzałów znikąd...
4Znów Waldek, tym razem na tarczy. Zagadki nie rozwiązał, ale przynajmniej uczciwie postawił sprawę.

5Niecałe 24 godziny przed terminem swoją odpowiedź nadesłał Rzast. Podoba mi się nietuzinkowe, probabilistyczne podejście do zagadnienia, ale w zagadce należało coś konkretnie udowodnić, a nie bawić się prawdopodobieństwami. Nie zaliczam.

P.S. Jeżeli natomiast chodzi o liczbę pi w liczbie pi, oraz stwierdzenie, że "im dłuższe rozwinięcie szukamy tym niższe prawdopodobieństwo znalezienia", to to jest nieprawdą, ponieważ dowolnej (skończonej) długości rozwinięcie liczby pi znajduje się w liczbie pi z prawdopodobieństwem 1. Podobnie jak wszystkie inne rodzaje informacji. Taki już urok nieskończoności.
Obstawiam, że chodziło bardziej o "czym dłuższe rozwinięcie, tym dalej trzeba szukać". Czyli na nasze, czym więcej drzew, tym dalej w las 🙂
6W ostatniej chwili, czyli wczoraj późnym wieczorem (godzinę przed północą, licząc według czasu polskiego) swoją ostatnią próbę podjął, tak dla odmiany, Waldek - tym razem w końcu się udało. Gratuluję zajadłości 🙂 Uff.
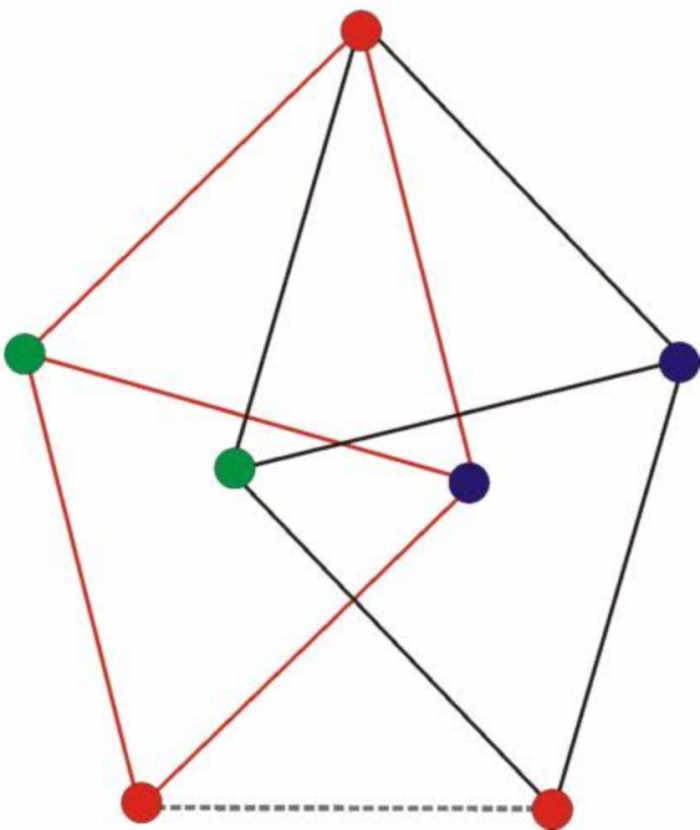
Przy odpowiednio dużej dozie uporu, obstawiam, Waldek mógłby spokojnie zabrać się za Hadwigera-Nelsona 🙂
Przyznam, że nie bardzo rozumiem o co w tym zadaniu kaman. No bo, z definicji punkt nie ma rozmiaru, z definicji, nawet odcinek o długości 1 mm ma nieskończenie wiele punktów. W rezultacie mając nieskończenie wiele punktów mamy nieskończenie wiele par punktów odległych od siebie o 1. Dowód jest prosty: nieskończoność to nieskończoność, nie ma nieskończoniści większej czy mniejszej czyli pomimo że kolorów jest trzy to w odległości akurat jeden jest ich nieskońćzenie dużo czyli tyle samo co np. w odległości 0.5.
Można też to udowodnić poprzez wykazanie, że w odległości jeden nie ma nieskończenie wiele punktów tego samego koloru. Nikt tego nie udowodni, bo zawsze jestem w stanie narysować wokół punktu np. białego, w odległości 1 nieskończenie wiele punktów białych. Dlaczego? Bo punkt nie ma rozmiaru i nawet jeśli wokół punktu białego w odległości 1 są same punkty czerwone to i tak wrysuję tam nieskończenie wiele punktów białych bo punkt nie ma rozmiaru czyli zawsze znajdę dla niego wolne miejsce.
Tym nie mniej zagadka w porzo, bo nic tak nie chroni przed stetryczeniem jak porządna porcja królowej nauk.
>> …bo zawsze jestem w stanie narysować wokół punktu np. białego, w odległości 1 nieskończenie wiele punktów białych.
W zagadce należy udowodnić możliwość (lub jej brak) pokolorowania każdego z punktów tak, aby żadna para punktów odległych o 1 nie współdzieliła tego samego koloru.
Prościutki przykład dla 9 kolorów polega na wypełnieniu płaszczyzny kwadratami w 9 kolorach, gdzie każdy kwadrat ma bok długości odrobinę powyżej 1/2, tak jak opisano to na przykład tutaj: https://mathlesstraveled.com/2018/06/02/the-chromatic-number-of-the-plane-part-4-an-upper-bound/
(dowody dla n=8 oraz 7 są nieco bardziej skomplikowane, nie chciało mi się szukać prawdę mówiąc).