(Dzisiejszy wpis miałem wrzucić dopiero w weekend, ale ponieważ komentatorzy się rozhasali jak nigdy, publikuję już dziś)
Pizzę trzema cięciami można pokroić na 4, 5, 6 lub 7 kawałków.
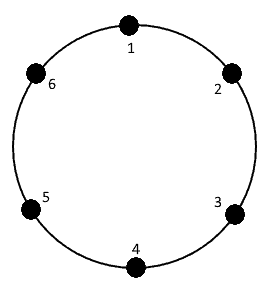
Zakładając numerację punktów jak na rysunku, cztery kawałki uzyskamy krojąc: (1-2,3-4,5-6) lub (2-3,4-5,6-7) lub (1-2,3-6,4-5) lub (1-6,2-5,3-4) lub (5-6,1-4,2-3)
Pięć kawałków: (5-6,1-3,2-4), (1-6,2-4,3-5), (1-2,3-5,4-6), (2-3,1-5,4-6), (3-4,1-5,2-6), (4-5,1-3,2-6)
Sześć kawałków: (1-4,2-6,3-5), (2-5,1-3,4-6), (3-6,1-5,2-4)
Siedem kawałków: (1-4,2-5,3-6)
Ponieważ każda kombinacja jest jednakowo prawdopodobna (robot losuje punkty i linie cięcia z rozkładem równomiernym), średnia liczba kawałków wynosi:
(5x4 + 6x5 + 3x6 + 1x7) / 15 = 75 / 15 = 5
Prawidłowej odpowiedzi jako pierwszy udzielił Butter, a zaraz po nim Cichy Fragles.
Publiczną próbę policzenia tego podjął Rzast i po kilku nieudanych podejściach (oraz podpowiedziach) trafił na właściwy trop. Fragles potwierdził w kolejnych komentarzach i wszyscy żyli długo i szczęśliwie.
Nagród, jak już nadmieniłem, nie mam 😉
„Siedem kawałków: (1-4,2-5,3-6)” – obojętnie z której strony podejdę to nie mogę podzielić pizzy na 7 kawałków
Jeżeli umieścisz wszystkie sześć punktów tak, że ich cięciwy przetną się w jednym punkcie, to faktycznie uzyskasz tylko sześć kawałków. Ale, jak już to opisał CF, prawdopodobieństwo takiego zdarzenia jest zerowe ze względu na to, że operujemy na liczbach rzeczywistych. Tym samym trzy cięciwy w środku zawsze utworzą trójkąt otoczony sześcioma kawałkami: https://i.imgur.com/oYaEAQ9.png
„z rozkładem równomiernym” – wziąłem to jako określenie potoczne, czyli, że punkty są w równej odległości od siebie – mój błąd.