Skarpetki w szufladzie: rozwiązanie zagadki + bonus

https://xpil.eu/318

Niedawno postawiłem tu pytanie: wyjmując po jednej skarpetce, ile średnio skarpetek wyjmiemy z szuflady zawierającej 10 różnych par skarpetek (niesparowanych!) aż natrafimy na parę z jedną ze skarpetek już wyjętych?

Problem nie jest całkiem trywialny, ale da się go rozpracować.

Najpierw pokażę jak krok po kroku policzyć tę wartość oczekiwaną, potem napiszemy sobie symulację i zobaczymy czy wynik wyjdzie podobny, a na koniec popatrzymy co dzieje się w przypadku ogólnym czyli N par skarpet zamiast dziesięciu.

Pierwsza skarpetka

Zaczynamy od pustej ręki i szuflady z 20 skarpetkami. Pierwsza wyciągnięta skarpetka nie będzie do niczego dopasowana, bo mamy pustą rękę.

Druga skarpetka

Wyciągamy z szuflady drugą skarpetkę. W ręce mamy już jedną. Jaka jest szansa, że ta druga jest taka sama, jak ta pierwsza (już wyjęta)?

Oczywiście 1/19 (spośród 19 skarpetek pozostałych w szufladzie tylko jedna pasuje do tej już wyjętej)

Trzecia skarpetka

No dobra, załóżmy, że z drugą skarpetką nie trafiliśmy. Mamy teraz w ręce dwie różne skarpetki, a w szufladzie - 18. Wyciągamy trzecią skarpetkę. Jaka jest szansa, że trafiliśmy w jedną z tych dwóch? Skoro w szufladzie są dwie pasujące, szansa jest 2/18.

Czy aby na pewno?

Nie. Szansa jest 2/18, pod warunkiem jednak, że nie trafiliśmy z drugą skarpetką. A skoro szansa powodzenia przy drugiej skarpetce była 1/19, to szansa niepowodzenia była 18/19 i przez tę właśnie liczbę należy przemnożyć nasze 2/18 żeby dostać prawdopodobieństwo trafienia w parę trzecią wyjętą z szuflady skarpetką.

A więc mamy 2/18 * 18/19

Czwarta skarpetka

Jeżeli trzy pierwsze skarpetki są wciąż nie do pary, wyciągamy czwartą.

Siedemnaście skarpet w szufladzie, z czego trzy pasują do tych, które już wyjęliśmy. Czyli 3/17. Ale oczywiście pod warunkiem, że dotychczas nie trafiliśmy, czyli:

3/17 * 18/19 * 16/18

Powoli zaczyna nam się wyłaniać jakiś wzorzec...

Piąta skarpetka

Po nieudanym wyjęciu czterech skarpetek mamy 16 w szufladzie, 4 w ręce.

Czyli 4/16 * 18/19 * 16/18 * 14/17

Jak widać z każdą kolejną skarpetką początkowy ułamek zmienia się tak, że licznik idzie w górę o jeden a mianownik o jeden w dół, a na końcu dokładamy kolejny ułamek z licznikiem o dwa mniejszym a mianownikiem o jeden mniejszym od poprzedniego:

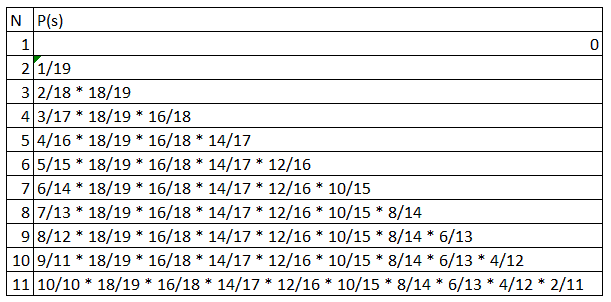
N - numer wyciąganej skarpetki, P(s) - prawdopodobieństwo sukcesu

No dobra. Znamy prawdopodobieństwa trafienia w parę dla kolejnych skarpetek...

A nie, nie znamy jeszcze. Teraz znamy:

Jak wyliczyć wartość oczekiwaną ilości wyjętych skarpet? Trzeba przemnożyć prawdopodobieństwa przez ilość skarpet w każdym kroku, po czym te iloczyny dodać:

0.105263157894737 + 0.315789473684211 + 0.594427244582043 + 0.86687306501548 + 1.04024767801858 + 1.04024767801858 + 0.853536556322934 + 0.548702071921886 + 0.249410032691766 + 0.0609668968802096 = 5.675464

5.675464

(jeżeli ktoś brzydzi się ułamkami dziesiętnymi i chciałby policzyć na piechotę z pierwszej tabelki, wyjdzie mu dokładnie $\frac{262144}{46189}$)

A więc średnio wyjmiemy z szuflady jakieś pięć, sześć skarpetek zanim trafimy na tę właściwą.

No dobra. Dużo gadania, ale właściwie jaka jest gwarancja, że powyższe rozważania nie są jedynie jakąś brednią? Sprawdźmy zatem doświadczalnie jak to z tymi skarpetkami naprawdę jest.

Jeżeli mam młotek, wszystko dookoła wygląda jak gwóźdź. Moim młotkiem jest PowerShell, w tym więc języku napiszemy sobie teraz prościutki skrypt sprawdzający powyższe rozważania empirycznie.

Lecimy!

$szuflada1 = New-Object System.Collections.ArrayList
1..10 | ForEach-Object { $szuflada1.add($_) | Out-Null; $szuflada1.add($_) | Out-Null; }
$ctr, $iter = 0, 1000
1..$iter | ForEach-Object {
    $szuflada2 = New-Object System.Collections.ArrayList
    $szuflada2.AddRange($szuflada1)
    $reka = New-Object System.Collections.ArrayList
    while ($true) {
        $idx = Get-Random -Minimum 0 -Maximum ($szuflada2.Count - 1)
        $skarpetka = $szuflada2[$idx]
        if ($reka.Contains($skarpetka)) {
            $ctr += ($reka.Count + 1)
            break
        }
        $reka.Add($skarpetka) | Out-Null
        $szuflada2.Remove($skarpetka) | Out-Null
    }
    Remove-Variable "szuflada2"
    Remove-Variable "reka"
}
$ctr / $iter

Powyższy skrypt powtarza doświadczenie z szufladą tysiąckrotnie, za każdym razem zapamiętuje przy której skarpetce trafiliśmy na dopasowanie, a na końcu podaje nam średnią z tego tysiąca prób.

Uruchomiłem go sobie kilka razy, dostałem na wyjściu:

5.615
5.651
5.636
5.765
5.626
5.649

Czyli pi razy oko się zgadza...

A teraz obiecany deser dla tych, którzy jeszcze nie przycięli komara. Mianowicie zobaczymy sobie teraz co się dzieje w przypadku ogólnym, czyli nie 10 skarpetek tylko N.

Nie będę (na szczęście!) opowiadał szczegółowo jak to się liczy, bo trochę za wysokie progi na moje nogi, podam tylko końcowy wynik.

Wartość oczekiwana w przypadku N par skarpet wynosi dokładnie:

$$\frac{4^N}{{2N \choose N}}$$

W mianowniku mamy symbol Newtona (jeżeli nie pamiętasz jak się to liczy, zapraszam do Wikipedii) - a w liczniku czwórkę podniesioną do N-tej potęgi.

A teraz niespodzianka: powyższe wyrażenie da się dla dużych N zastąpić o wiele prostszym:

$$\sqrt{\pi N}$$

Skąd się tu pod tym pierwiastkiem wzięło Pi skoro ani szuflada nie jest okrągła ani skarpetki - proszę nie pytać, jednak przybliżenie jest bardzo dobre i tym lepsze, im większe N przyjmiemy. Sprawdźmy to sobie za pomocą Wolfram Alpha:

Przy stu parach skarpetek różnica spada do około dwóch setnych:

Magia, panie...