Potrójny Fibonacci i 2023 – rozwiązanie zagadki

https://xpil.eu/s3f 📋

Jako że jestem osobnikiem do immentu leniwym a także niezbyt rozgarniętym, niedawno postawioną zagadkę rozwiązałem zoologicznie, czyli Pythonem:

Kod wygląda o, tak:

rok = 2023
minimalna_suma = rok
for istart in range(rok):
    if(istart >= minimalna_suma):
        break
    for jstart in range(istart+1, rok):
        if(istart + jstart >= minimalna_suma):
            break
        for kstart in range(jstart+1, rok):
            if (istart + jstart + kstart >= minimalna_suma):
                break
            ciag = [i, j, k] = [istart, jstart, kstart]
            while i + j + k <= rok:
                i, j, k = j, k, i + j + k
                ciag.append(k)
            if (k == rok):
                minimalna_suma = istart + jstart + kstart
                wynik = ciag
print(f'{minimalna_suma}, {wynik}')

Powyższy skrypt wypisał mi na wyjściu:

15, [1, 6, 8, 15, 29, 52, 96, 177, 325, 598, 1100, 2023]

Rozwiązanie zagadki to 1, 6, 8 (suma 15). Istotnie, ciąg zaczynający się od 1, 6, 8 zawiera liczbę 2023 (jak widać powyżej), a suma tych trzech liczb (15) jest najmniejszą z możliwych.

Nie byłbym sobą gdybym nie zerknął jak sytuacja wygląda dla innych numerów lat. Po drobnej modyfikacji powyższego skryptu...

for rok in range(1950, 2101):
    limit, minimalna_suma = rok // 3, rok + 1
    for istart in range(limit):
        if(istart >= minimalna_suma):
            break
        for jstart in range(istart+1, limit):
            if(istart + jstart >= minimalna_suma):
                break
            for kstart in range(jstart+1, limit):
                if (istart + jstart + kstart >= minimalna_suma):
                    break
                ciag = [i, j, k] = [istart, jstart, kstart]
                while i + j + k <= rok:
                    i, j, k = j, k, i + j + k
                    ciag.append(k)
                if (k == rok):
                    minimalna_suma = istart + jstart + kstart
                    wynik = ciag
    print(f'{rok}, {minimalna_suma}, {wynik}')

... dostałem taką odpowiedź:

1950, 26, [0, 12, 14, 26, 52, 92, 170, 314, 576, 1060, 1950]
1951, 47, [2, 11, 34, 47, 92, 173, 312, 577, 1062, 1951]
1952, 26, [1, 9, 16, 26, 51, 93, 170, 314, 577, 1061, 1952]
1953, 28, [5, 10, 13, 28, 51, 92, 171, 314, 577, 1062, 1953]
1954, 26, [2, 6, 18, 26, 50, 94, 170, 314, 578, 1062, 1954]
1955, 15, [2, 6, 7, 15, 28, 50, 93, 171, 314, 578, 1063, 1955]
1956, 46, [2, 4, 40, 46, 90, 176, 312, 578, 1066, 1956]       
1957, 27, [2, 12, 13, 27, 52, 92, 171, 315, 578, 1064, 1957]
1958, 47, [2, 10, 35, 47, 92, 174, 313, 579, 1066, 1958]   
1959, 27, [3, 9, 15, 27, 51, 93, 171, 315, 579, 1065, 1959]
1960, 25, [0, 5, 20, 25, 50, 95, 170, 315, 580, 1065, 1960]
1961, 27, [4, 6, 17, 27, 50, 94, 171, 315, 580, 1066, 1961]
1962, 25, [1, 2, 22, 25, 49, 96, 170, 315, 581, 1066, 1962]
1963, 26, [0, 11, 15, 26, 52, 93, 171, 316, 580, 1067, 1963]
1964, 47, [1, 12, 34, 47, 93, 174, 314, 581, 1069, 1964]    
1965, 26, [1, 8, 17, 26, 51, 94, 171, 316, 581, 1068, 1965]
1966, 14, [0, 5, 9, 14, 28, 51, 93, 172, 316, 581, 1069, 1966]
1967, 26, [2, 5, 19, 26, 50, 95, 171, 316, 582, 1069, 1967]
1968, 46, [0, 8, 38, 46, 92, 176, 314, 582, 1072, 1968]
1969, 46, [1, 5, 40, 46, 91, 177, 314, 582, 1073, 1969]
1970, 14, [1, 2, 11, 14, 27, 52, 93, 172, 317, 582, 1071, 1970]
1971, 47, [1, 11, 35, 47, 93, 175, 315, 583, 1073, 1971]   
1972, 27, [3, 8, 16, 27, 51, 94, 172, 317, 583, 1072, 1972]
1973, 25, [0, 4, 21, 25, 50, 96, 171, 317, 584, 1072, 1973]
1974, 27, [4, 5, 18, 27, 50, 95, 172, 317, 584, 1073, 1974]
1975, 46, [0, 7, 39, 46, 92, 177, 315, 584, 1076, 1975]
1976, 26, [0, 10, 16, 26, 52, 94, 172, 318, 584, 1074, 1976]
1977, 28, [4, 11, 13, 28, 52, 93, 173, 318, 584, 1075, 1977]
1978, 26, [1, 7, 18, 26, 51, 95, 172, 318, 585, 1075, 1978]
1979, 8, [1, 2, 5, 8, 15, 28, 51, 94, 173, 318, 585, 1076, 1979]
1980, 26, [2, 4, 20, 26, 50, 96, 172, 318, 586, 1076, 1980]
1981, 48, [2, 13, 33, 48, 94, 175, 317, 586, 1078, 1981]
1982, 46, [0, 6, 40, 46, 92, 178, 316, 586, 1080, 1982]
1983, 27, [2, 10, 15, 27, 52, 94, 173, 319, 586, 1078, 1983]
1984, 29, [6, 11, 12, 29, 52, 93, 174, 319, 586, 1079, 1984]
1985, 27, [3, 7, 17, 27, 51, 95, 173, 319, 587, 1079, 1985]
1986, 25, [0, 3, 22, 25, 50, 97, 172, 319, 588, 1079, 1986]
1987, 48, [1, 15, 32, 48, 95, 175, 318, 588, 1081, 1987]
1988, 48, [2, 12, 34, 48, 94, 176, 318, 588, 1082, 1988]
1989, 26, [0, 9, 17, 26, 52, 95, 173, 320, 588, 1081, 1989]
1990, 14, [0, 4, 10, 14, 28, 52, 94, 174, 320, 588, 1082, 1990]
1991, 26, [1, 6, 19, 26, 51, 96, 173, 320, 589, 1082, 1991]
1992, 16, [4, 5, 7, 16, 28, 51, 95, 174, 320, 589, 1083, 1992]
1993, 26, [2, 3, 21, 26, 50, 97, 173, 320, 590, 1083, 1993]
1994, 27, [1, 12, 14, 27, 53, 94, 174, 321, 589, 1084, 1994]
1995, 48, [2, 11, 35, 48, 94, 177, 319, 590, 1086, 1995]
1996, 27, [2, 9, 16, 27, 52, 95, 174, 321, 590, 1085, 1996]
1997, 29, [6, 10, 13, 29, 52, 94, 175, 321, 590, 1086, 1997]
1998, 27, [3, 6, 18, 27, 51, 96, 174, 321, 591, 1086, 1998]
1999, 25, [0, 2, 23, 25, 50, 98, 173, 321, 592, 1086, 1999]
2000, 47, [2, 4, 41, 47, 92, 180, 319, 591, 1090, 2000]
2001, 28, [3, 12, 13, 28, 53, 94, 175, 322, 591, 1088, 2001]
2002, 26, [0, 8, 18, 26, 52, 96, 174, 322, 592, 1088, 2002]
2003, 15, [2, 4, 9, 15, 28, 52, 95, 175, 322, 592, 1089, 2003]
2004, 26, [1, 5, 20, 26, 51, 97, 174, 322, 593, 1089, 2004]
2005, 28, [5, 6, 17, 28, 51, 96, 175, 322, 593, 1090, 2005]
2006, 47, [1, 6, 40, 47, 93, 180, 320, 593, 1093, 2006]
2007, 27, [1, 11, 15, 27, 53, 95, 175, 323, 593, 1091, 2007]
2008, 48, [1, 12, 35, 48, 95, 178, 321, 594, 1093, 2008]
2009, 27, [2, 8, 17, 27, 52, 96, 175, 323, 594, 1092, 2009]
2010, 29, [6, 9, 14, 29, 52, 95, 176, 323, 594, 1093, 2010]
2011, 27, [3, 5, 19, 27, 51, 97, 175, 323, 595, 1093, 2011]
2012, 25, [0, 1, 24, 25, 50, 99, 174, 323, 596, 1093, 2012]
2013, 47, [1, 5, 41, 47, 93, 181, 321, 595, 1097, 2013]
2014, 14, [0, 3, 11, 14, 28, 53, 95, 176, 324, 595, 1095, 2014]
2015, 26, [0, 7, 19, 26, 52, 97, 175, 324, 596, 1095, 2015]
2016, 28, [4, 8, 16, 28, 52, 96, 176, 324, 596, 1096, 2016]
2017, 26, [1, 4, 21, 26, 51, 98, 175, 324, 597, 1096, 2017]
2018, 27, [0, 13, 14, 27, 54, 95, 176, 325, 596, 1097, 2018]
2019, 47, [0, 7, 40, 47, 94, 181, 322, 597, 1100, 2019]
2020, 27, [1, 10, 16, 27, 53, 96, 176, 325, 597, 1098, 2020]
2021, 29, [5, 11, 13, 29, 53, 95, 177, 325, 597, 1099, 2021]
2022, 27, [2, 7, 18, 27, 52, 97, 176, 325, 598, 1099, 2022]
2023, 15, [1, 6, 8, 15, 29, 52, 96, 177, 325, 598, 1100, 2023]
2024, 27, [3, 4, 20, 27, 51, 98, 176, 325, 599, 1100, 2024]
2025, 49, [2, 13, 34, 49, 96, 179, 324, 599, 1102, 2025]
2026, 47, [0, 6, 41, 47, 94, 182, 323, 599, 1104, 2026]
2027, 15, [2, 3, 10, 15, 28, 53, 96, 177, 326, 599, 1102, 2027]
2028, 26, [0, 6, 20, 26, 52, 98, 176, 326, 600, 1102, 2028]
2029, 28, [4, 7, 17, 28, 52, 97, 177, 326, 600, 1103, 2029]
2030, 26, [1, 3, 22, 26, 51, 99, 176, 326, 601, 1103, 2030]
2031, 27, [0, 12, 15, 27, 54, 96, 177, 327, 600, 1104, 2031]
2032, 49, [2, 12, 35, 49, 96, 180, 325, 601, 1106, 2032]
2033, 27, [1, 9, 17, 27, 53, 97, 177, 327, 601, 1105, 2033]
2034, 29, [5, 10, 14, 29, 53, 96, 178, 327, 601, 1106, 2034]
2035, 27, [2, 6, 19, 27, 52, 98, 177, 327, 602, 1106, 2035]
2036, 16, [3, 6, 7, 16, 29, 52, 97, 178, 327, 602, 1107, 2036]
2037, 48, [2, 5, 41, 48, 94, 183, 325, 602, 1110, 2037]
2038, 14, [0, 2, 12, 14, 28, 54, 96, 178, 328, 602, 1108, 2038]
2039, 49, [2, 11, 36, 49, 96, 181, 326, 603, 1110, 2039]
2040, 28, [3, 9, 16, 28, 53, 97, 178, 328, 603, 1109, 2040]
2041, 26, [0, 5, 21, 26, 52, 99, 177, 328, 604, 1109, 2041]
2042, 28, [4, 6, 18, 28, 52, 98, 178, 328, 604, 1110, 2042]
2043, 26, [1, 2, 23, 26, 51, 100, 177, 328, 605, 1110, 2043]
2044, 27, [0, 11, 16, 27, 54, 97, 178, 329, 604, 1111, 2044]
2045, 29, [4, 12, 13, 29, 54, 96, 179, 329, 604, 1112, 2045]
2046, 27, [1, 8, 18, 27, 53, 98, 178, 329, 605, 1112, 2046]
2047, 15, [1, 5, 9, 15, 29, 53, 97, 179, 329, 605, 1113, 2047]
2048, 27, [2, 5, 20, 27, 52, 99, 178, 329, 606, 1113, 2048]
2049, 48, [0, 9, 39, 48, 96, 183, 327, 606, 1116, 2049]
2050, 48, [1, 6, 41, 48, 95, 184, 327, 606, 1117, 2050]
2051, 28, [2, 11, 15, 28, 54, 97, 179, 330, 606, 1115, 2051]
2052, 49, [1, 12, 36, 49, 97, 182, 328, 607, 1117, 2052]
2053, 28, [3, 8, 17, 28, 53, 98, 179, 330, 607, 1116, 2053]
2054, 26, [0, 4, 22, 26, 52, 100, 178, 330, 608, 1116, 2054]
2055, 28, [4, 5, 19, 28, 52, 99, 179, 330, 608, 1117, 2055]
2056, 48, [0, 8, 40, 48, 96, 184, 328, 608, 1120, 2056]
2057, 27, [0, 10, 17, 27, 54, 98, 179, 331, 608, 1118, 2057]
2058, 29, [4, 11, 14, 29, 54, 97, 180, 331, 608, 1119, 2058]
2059, 27, [1, 7, 19, 27, 53, 99, 179, 331, 609, 1119, 2059]
2060, 8, [0, 3, 5, 8, 16, 29, 53, 98, 180, 331, 609, 1120, 2060]
2061, 27, [2, 4, 21, 27, 52, 100, 179, 331, 610, 1120, 2061]
2062, 14, [0, 1, 13, 14, 28, 55, 97, 180, 332, 609, 1121, 2062]
2063, 48, [0, 7, 41, 48, 96, 185, 329, 610, 1124, 2063]
2064, 28, [2, 10, 16, 28, 54, 98, 180, 332, 610, 1122, 2064]
2065, 30, [6, 11, 13, 30, 54, 97, 181, 332, 610, 1123, 2065]
2066, 28, [3, 7, 18, 28, 53, 99, 180, 332, 611, 1123, 2066]
2067, 15, [0, 7, 8, 15, 30, 53, 98, 181, 332, 611, 1124, 2067]
2068, 49, [3, 4, 42, 49, 95, 186, 330, 611, 1127, 2068]
2069, 50, [2, 13, 35, 50, 98, 183, 331, 612, 1126, 2069]
2070, 27, [0, 9, 18, 27, 54, 99, 180, 333, 612, 1125, 2070]
2071, 15, [1, 4, 10, 15, 29, 54, 98, 181, 333, 612, 1126, 2071]
2072, 27, [1, 6, 20, 27, 53, 100, 180, 333, 613, 1126, 2072]
2073, 29, [5, 7, 17, 29, 53, 99, 181, 333, 613, 1127, 2073]
2074, 27, [2, 3, 22, 27, 52, 101, 180, 333, 614, 1127, 2074]
2075, 28, [1, 12, 15, 28, 55, 98, 181, 334, 613, 1128, 2075]
2076, 50, [2, 12, 36, 50, 98, 184, 332, 614, 1130, 2076]
2077, 28, [2, 9, 17, 28, 54, 99, 181, 334, 614, 1129, 2077]
2078, 30, [6, 10, 14, 30, 54, 98, 182, 334, 614, 1130, 2078]
2079, 28, [3, 6, 19, 28, 53, 100, 181, 334, 615, 1130, 2079]
2080, 26, [0, 2, 24, 26, 52, 102, 180, 334, 616, 1130, 2080]
2081, 49, [2, 5, 42, 49, 96, 187, 332, 615, 1134, 2081]
2082, 29, [3, 12, 14, 29, 55, 98, 182, 335, 615, 1132, 2082]
2083, 27, [0, 8, 19, 27, 54, 100, 181, 335, 616, 1132, 2083]
2084, 9, [2, 3, 4, 9, 16, 29, 54, 99, 182, 335, 616, 1133, 2084]
2085, 27, [1, 5, 21, 27, 53, 101, 181, 335, 617, 1133, 2085]
2086, 29, [5, 6, 18, 29, 53, 100, 182, 335, 617, 1134, 2086]
2087, 49, [1, 7, 41, 49, 97, 187, 333, 617, 1137, 2087]
2088, 28, [1, 11, 16, 28, 55, 99, 182, 336, 617, 1135, 2088]
2089, 30, [5, 12, 13, 30, 55, 98, 183, 336, 617, 1136, 2089]
2090, 28, [2, 8, 18, 28, 54, 100, 182, 336, 618, 1136, 2090]
2091, 15, [0, 6, 9, 15, 30, 54, 99, 183, 336, 618, 1137, 2091]
2092, 28, [3, 5, 20, 28, 53, 101, 182, 336, 619, 1137, 2092]
2093, 26, [0, 1, 25, 26, 52, 103, 181, 336, 620, 1137, 2093]
2094, 49, [1, 6, 42, 49, 97, 188, 334, 619, 1141, 2094]
2095, 15, [1, 3, 11, 15, 29, 55, 99, 183, 337, 619, 1139, 2095]
2096, 27, [0, 7, 20, 27, 54, 101, 182, 337, 620, 1139, 2096]
2097, 29, [4, 8, 17, 29, 54, 100, 183, 337, 620, 1140, 2097]
2098, 27, [1, 4, 22, 27, 53, 102, 182, 337, 621, 1140, 2098]
2099, 28, [0, 13, 15, 28, 56, 99, 183, 338, 620, 1141, 2099]
2100, 49, [0, 8, 41, 49, 98, 188, 335, 621, 1144, 2100]

A jak Wam poszło? Całkiem nieźle! Zagadka była naprawdę prosta, więc tym razem nie ma żadnych błędnych rozwiązań, ale i tak jest interesująco.

1Cichy był pierwszy, z poprawną odpowiedzią (1, 6, 8) wyliczoną skryptem.

Znalezione przez skrypt, analitycznie nie chciało mi się kombinować.

-- Cichy, grudzień 2022

2Tego samego dnia pod wieczór odezwał się Waldek, głosem germańskiego oprawcy łamane przez najeźdźcy:

3Nazajutrz rano przyszło rozwiązanie Krzyśka. Prawidłowe, z załączonym kodem w Pythonie:

WANTED = 2023


def make_seq(a, b, c):
    cache = {0: a, 1: b, 2: c}

    def f(n):
        try:
            return cache[n]
        except KeyError:
            an = f(n - 1) + f(n - 2) + f(n - 3)
            cache[n] = an
            return an

    return f


best_score = WANTED + 1
best = (0, 0, 0)

for a in range(0, WANTED // 3):
    for b in range(a + 1, best_score - a):
        for c in range(b + 1, best_score - a - b):
            seq = make_seq(a, b, c)
            for n in range(3, WANTED):
                an = seq(n)
                if an > WANTED:
                    break
                if an == WANTED:
                    score = a + b + c
                    if score < best_score:
                        best_score = score
                        best = (a, b, c)
                        print(best, best_score, n)
                    break

Skrypt Krzyśka wypluł takie coś:

(0, 1, 505) 506 5
(0, 7, 283) 290 6
(0, 9, 148) 157 7
(0, 19, 30) 49 9
(1, 6, 8) 15 11

Ostatnia linijka pokazuje poprawne rozwiązanie. Zaliczam.

4Czwartym rozwiązującym był Rozie, który też poradził sobie prostym skryptem w Pythonie. Warto zauważyć, że skrypt Roziego jest o trzy linijki szczuplejszy od mojego :

def find_next_fibo(a):
    new = sum(a[-3:])
    return new


for a in range(0, 20):
    for b in range(a + 1, 20):
        for c in range(b + 1, 20):
            fibo = []
            fibo.append(a)
            fibo.append(b)
            fibo.append(c)
            while fibo[-1:][0] < 2023:
                fibo.append(find_next_fibo(fibo))
            if 2023 in fibo:
                print(fibo)

Wynik:

[1, 6, 8, 15, 29, 52, 96, 177, 325, 598, 1100, 2023]
[6, 8, 15, 29, 52, 96, 177, 325, 598, 1100, 2023]

Nie byłbym sobą gdybym nie zerknął w wydajność obydwu skryptów. Okazuje się, że czas wykonania skryptu Roziego jest odrobinę dłuższy od mojego (Rozie: 0.16 sekundy, mój: 0.03 sekundy, testowane na Pythonie 3.11, żadne tam PyPy)), chociaż na pierwszy rzut oka wykonuje dużo mniej instrukcji od mojego. Oto porównanie:

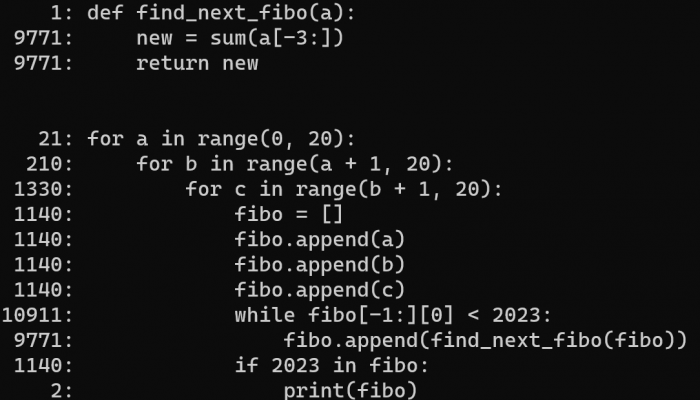
Jak widać u mnie jedna z linii wykonała się prawie 30 tys. razy, a dwie sąsiednie po 24 tysiące - u Roziego "tylko" 19 tysięcy w pętli główej i drugie tyle w funkcji find_next_fibo. Nie chciało mi się już wgryzać w czasy wykonania poszczególnych linii, ale domyślam się, że operacja dołączenia do listy fibo wyniku działania funkcji find_next_fibo jest po prostu wolniejsza, a do tego dochodzi jeszcze każdorazowe sumowanie trzech ostatnich elementów w samym ciele funkcji. A ja w swoim skrypcie przechowuję do sumowania zawsze tylko trzy ostatnie elementy ciągu i żadnych funkcji nie wołam.

Bardzo fajnie na tym tle wypada za to skrypt Krzyśka (patrz trójka powyżej), który z moim idzie łeb w łeb jeśli chodzi o prędkość działania, chociaż paradoksalnie wykonuje niektóre linie nie dziesiątki, ale setki tysięcy razy:

Myślę, że takie szybkie działanie skryptu Krzyśka wynika po pierwsze z zastosowania słownika (zamiast listy) w ciele funkcji make_seq, a po drugie z bardziej sprytnego podejścia do zmiennych kontrolnych pętli w części głównej. Nie będę kłamał, nie do końca rozumiem jak ten skrypt tak naprawdę działa (mea culpa: nie miałem już wystarczająco dużo rozpędu żeby się weń porządnie wgryźć), ale działa wyśmienicie.

5Nazajutrz odezwał się Rzast, który jako pierwszy z rozwiązujących użył do rozwiązania zagadki Excela. Zbudowawszy całkiem zaawansowany karkusz okraszony jeszcze bardziej zawiłym opisem, Rzast uzyskał jak najbardziej poprawny wynik. Zaliczam!

6W przedwigilijny piątek wieczorem swoje rozwiązanie przysłał Tywan:

I do kompletu kod w Ruby:

SUM = 2023
# zwraca pelna sekwencje jesli daje ona oczekiwany rezultat
def test(seq)
  loop {
    sum = seq[-1] + seq[-2] + seq[-3]
    seq.push sum
    return nil if sum > SUM
    return seq if sum == SUM
  }
end

minSum = SUM + 1

# wypisuje najlepsze rozwiazania
(0..).each{|a0|
  break if 3*a0 > minSum
  ((a0+1)..).each{|a1|
    break if a0+2*a1 > minSum
    ((a1+1)..).each{|a2|
      sum = a0 + a1 + a2
      break if sum > minSum
      if r = test([a0, a1, a2])
        puts "#{sum} #{r}"
        minSum = sum if sum < minSum
        break
      end
    }
  }
}

https://xpil.eu/s3f 📋