Uwaga: podczas tworzenia tego wpisu bawiłem się na boku programem Excalidraw. Jeżeli którekolwiek z poniższych diagramów wprawiają cię w zakłopotanie, skonsultuj się z lekarzem lub farmaceutą.
Jak wygląda ciąg Fibonacciego - wszyscy wiedzą. Zaczynamy od 0, 1, a każdy kolejny element to suma dwóch poprzednich: 0,1,1,2,3,5,8,13,21,...

Oczywiście nie musimy zaczynać od 0,1. Możemy zacząć od dowolnej innej pary liczb naturalnych, na przykład 7, 11, 18, 29, 47... Nie jest to już co prawda ciąg Fibonacciego tylko "fibonacciopodobny", ale ciąg to ciąg.
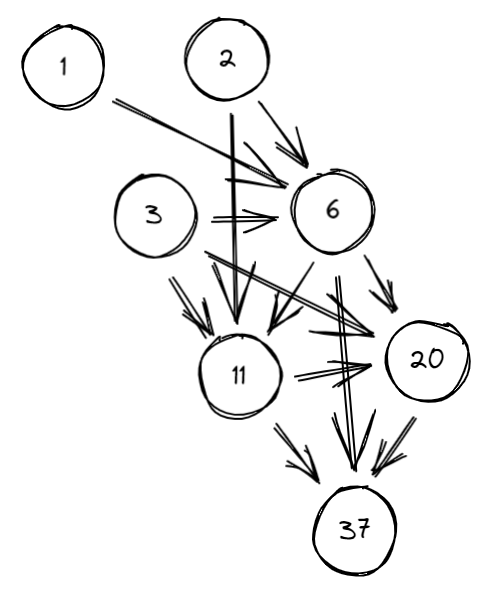
A co jeżeli kolejny element zdefiniować jako sumę trzech poprzednich liczb a nie dwóch? Rzecz jasna trzeba wówczas zacząć od trójki liczb. Na przykład startując od 1, 2, 3 dostaniemy: 1, 2, 3, 6, 11, 20, 37, ...
A zaczynając od 0, 1000, 1023 dostaniemy: 0, 1000, 1023, 2023, 4046, ...
W tym ostatnim przypadku widzimy, że jednym z elementów ciągu jest 2023, czyli numer nadchodzącego już za kilkanaście dni nowego roku.
No i teraz pytanie: od jakich liczb należy zacząć taki "potrójny ciąg Fibonacciego", żeby: (A) liczba 2023 pojawiła się wśród wyrazów ciągu oraz (B) suma trzech pierwszych wyrazów była możliwie najmniejsza? Proszę dodatkowo założyć, że trzy pierwsze elementy ciągu muszą być różne, więc na przykład odpada ciąg zaczynający się od 0,0,1 albo 23, 1000, 1000 - ale 23, 999, 1001 już może być. Dla uniknięcia niejednoznaczności proszę również założyć, że ciąg jest rosnący.
P.S. W tytule wyraźnie sugeruję rozwiązanie za pomocą komputera, ale jeżeli dasz radę machnąć to analitycznie - szacun.
Rozwiązanie zagadki tutaj.
