Zaczniemy od tego, o czym już wcześniej wspominałem:
2025 to jedyny kwadrat w tym stuleciu. Poprzedni był w 1936, a następny dopiero w 2116:
$$45^2=2025$$
Czego jednak wcześniej nie zauważyłem, to to, że 45 da się przedstawić jako 20+25. Tym samym mamy więc:
$$(20+25)^2=2025$$
2025 jest sumą wszystkich liczb nieparzystych od 1 do 89:
$$1+3+5+...+87+89=2025$$
2025 jest sumą wszystkich sześcianów od 1 do 9:
$$1^3+2^3+...+8^3+9^3=2025$$
2025 jest najmniejszą możliwą wartością promienia półokręgu o promieniu r, w który można wpisać cztery koła spełniające następujące warunki:
- dwie pary kół z identycznymi promieniami (a więc dwa koła o promieniu \(r_1\) oraz dwa inne koła o promieniu \(r_2\))
- wszystkie koła są styczne albo do półokręgu, albo do innych kół, albo do pewnej cięciwy tego półokręgu
- wszystkie promienie (a więc: \(r, r_1, r_2\)) są liczbami naturalnymi.
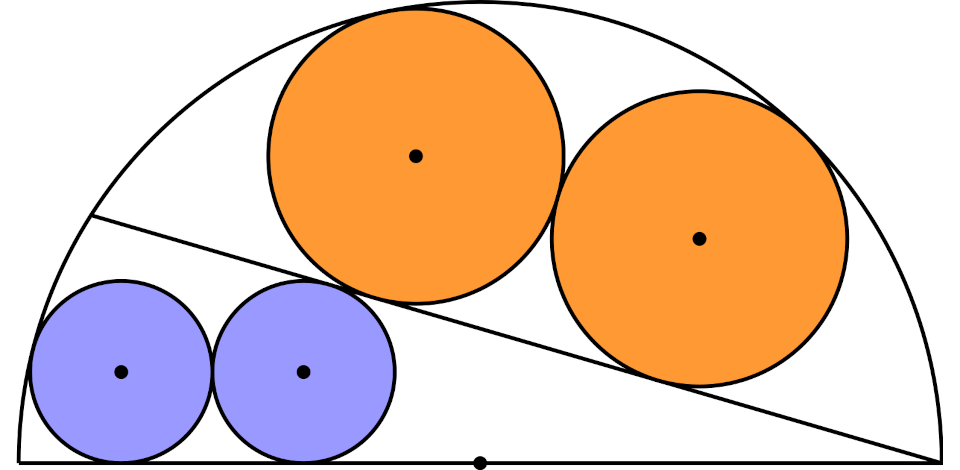
Promień półokręgu to 2025, a promienie wpisanych kół to 400 oraz 648 (i bez ułamków mniej się nie da).
Jeżeli stworzymy liczbę postaci:
122333444455555... aż do 45 powtórzonego 45 razy, dostaniemy w wyniku liczbę, która ma 2025 cyfr, a jak już nadmieniłem \(45^2=2025\). Jest to jedyna taka liczba.
2025 jest największą obecnie znaną liczbą, która - sama będąc kwadratem - pozostanie kwadratem po zwiększeniu każdej cyfry o 1: \(\sqrt{3136}=56\).
2025 liczb naturalnych między 1 a 9999 ma ostatnią cyfrę większą od pozostałych. Uwaga: liczby mniejsze od tysiąca wypełniamy od lewej strony zerami, o tak: 0001, 0002, 0003, ...
Okrąg o promieniu 26 nałożony na siatkę kwadratów o boku 1 (z centralnym kwadratem pośrodku okręgu) obejmuje dokładnie 2025 kwadratów:
Promień: 2, Liczba kwadratów: 5
Jeżeli podniesiemy 2025 do kwadratu, dostaniemy 4100625. 41+625=666 (liczba Bestii!). Jest to póki co jedyna znana liczba z tą własnością.
Cztery najmniejsze naturalne liczby złożone to 4, 6, 8, 9. Jeżeli zbudujemy z nich macierz 4x4, przesuwając w każdym wierszu liczby cyklicznie, dostaniemy:
$$\begin{bmatrix}
4 & 6 & 8 & 9 \\
9 & 4 & 6 & 8 \\
8 & 9 & 4 & 6 \\
6 & 8 & 9 & 4 \\
\end{bmatrix}$$
Wyznacznik tej macierzy to -2025.
2025 da się zapisać jako sumę dwóch kwadratów dokładnie na jeden sposób:
$$2025 = 27^2 + 36^2$$
\(2^{2025}+1\) dzieli się przez \(2\times2025+1\).
2025 jest 23. z kolei liczbą oktagonalną. Liczymy kropki na bokach rosnących ośmiokątów foremnych, zgodnie z przykładem poniżej. Aby uzyskać 2025, potrzebujemy dwudziestu trzech takich ośmiokątów (tak naprawdę dwudziestu dwóch, chyba żeby potraktować kropkę w samym środku jako ośmiokąt zdegenerowany).
Liczba punktów: 1
Powyższe informacje oraz obrazki bezczelnie ukradłem z tej strony.
Jako, że Σ(n=1…9) = 45 to też:
(1+2+3+…+9)² = 2025
Z ciekawości sprawdziłem, okazuje się, że można w komentarzach używać składni LaTeX:
\(\sum_{n=1}^{9} n\)Efekt:
\( \sum_{n=1}^{9} n \)
$$a^{b^c}$$
Okazuje się, że składnia z podwójnymi dolarami też działa:
Testujemy LaTeX inline: $\sqrt{4}=\pm 2$
Ale z pojedynczymi już nie.
Dzięki za te ciekawostki. Wykorzystam je na pierwszej lekcji matmy po przerwie świątecznej, dla rozgrzewki. 🙂
Czeszę się bardzo. W międzyczasie udało mi się (z wydatną pomocą LLM-a) dodać element interaktywny do jednej z sekcji.
Zauważyłem dodatkowy kwadracik między tymi kwadratami.
2025 = 45×45, a równocześnie 25 = 5×5.
Ale w poprzednich stuleciach wyglądało to inaczej
1936 to 44×44 ale równocześnie 36=6×6
1849 to 43×43 ale 49 to 7×7 … czyli co stulecie wcześniej jest to kwadrat większej liczby a więc 1764 = 42×42 ale 64 to 8×8.
Faktycznie. I w drugą stronę też działa, aż do 60.