Połamana zagadka – rozwiązanie

https://xpil.eu/6i7 📋

Pierwsza część zagadki jest dość prosta.

Najpierw zauważamy, że przy zadanej z góry ilości segmentów zawsze najlepiej podzielić patyk na kawałki o równej długości.

Skąd o tym wiemy?

Sprawdźmy dla dwóch kawałków (a więc przyjmijmy długość patyka = 2x):

Jeżeli są równe, każdy z nich ma długość x, a więc iloczyn = x².

Jeżeli nie są równe, to długość jednego z nich wynosi (x-a), a drugiego (x+a). Iloczyn to x²-a², czyli mniej niż x².

Dla trzech i więcej kawałków wychodzi podobnie - zasadniczo sprowadza się to do szukania optymalnych prostopadłościanów w trzech i więcej wymiarach - zawsze się okaże, że maksimum objętości przypada na bryłę o jednakowej długości krawędziach (sześcian, tesserakt itd). Alternatywnie można skorzystać z nierówności Cauchy'ego-Schwarza.

No dobra. Spróbujmy teraz posprawdzać różne połamania. Zaczniemy od jednego kawałka: 10.

Dwa kawałki: 5*5=25

Trzy: 10/3*10/3*10/3 = 37.(037)

Cztery: 2.5⁴=39 1/16

Ciągle rośnie, ale jakby coraz wolniej. Sprawdzamy dalej:

Pięć kawałków: 2⁵=32

Sześć: niecałe 21.5.

Aha, czyli od piątki już maleje. Wygląda na to, że maksimum jest dla czterech kawałków.

Czyli cztery kawałki to nasze rozwiązanie (bo ułamkowe ilości kawałków nie wchodzą w rachubę...). Cztery kawałki, każdy długi na 2.5, a iloczyn to 39 z niedużym hakiem.

A jeżeli długość patyka wzrośnie do 100? Jak to ugryźć?

Można mnożyć na piechotę, ale zaraz się okaże, że wychodzą strasznie wielkie liczby.

Trzeba pójść po rozum do głowy...

Jeżeli podzielimy patyk o długości D na N równych części, każda część będzie miała długość D/N, a ich iloczyn to (D/N)^N. Oznaczmy długość pojedynczego kawałka przez L, gdzie L=D/N - widzimy teraz, że iloczyn długości to L^N. Zauważamy też, że N = D/L, a więc nasz iloczyn można zapisać jako L^D/L_. Ponieważ D jest stałe, problem sprowadza się do znalezienia takiego L, które daje maksymalną wartość wyrażenia L^1/L.

Widzicie w tym coś ciekawego? Mi się podoba to, że niezależnie od długości patyka optimum zależy wyłącznie od długości pojedynczego kawałka.

Jak policzyć maksimum funkcji f(x) = x^1/x ?

Można to zrobić klasycznie, ale wtedy zaplączemy się w logarytmach (nie da się policzyć pochodnej f(x) bez używania logarytmów). Ale można też zauważyć, że:

e^x>1+x dla x≠0

e^x=1+x dla x=0

Stąd mamy bezpośrednio:

(1) e^(x−e)/e>1+(x−e)/e dla (x−e)/e ≠0

(2) e^(x−e)/e=1+(x−e)/e dla (x−e)/e =0

Prawą stronę (1) można uprościć do x/e. A więc (1) można (po przemnożeniu obu stron przez e) zapisać jako:

(3) e^x/e>x, po podniesieniu obu stron do potęgi 1/x dostajemy: e^1/e>x^1/x dla (x-e)/e≠0

Skoro z (1) wyszło nam (3), to (2) analogicznie daje nam:

(4) e^1/e=x^1/x dla (x-e)/e=0 (czyli dla x=e)

Pokazaliśmy zatem, że f(x) jest zawsze mniejsza od e^1/e z wyjątkiem x=e, czyli f(x) przyjmuje maximum dla x=e. Innymi słowy długość pojedynczego segmentu powinna być możliwie najbliższa e≈2.7182... Jeżeli do tego dołożymy warunek, że kawałki muszą być sobie równe, wychodzi na to, że 2.5 jest faktycznie optymalne dla długości 10.

A dla długości 100?

100/e ≈ 36.79

A więc podzielenie patyka o długości 100 na 37 równych części da największy możliwy iloczyn - i to jest poprawna odpowiedź na drugą część zagadki.

Jeszcze tylko szybciutkie sprawdzenie w Wolframie:

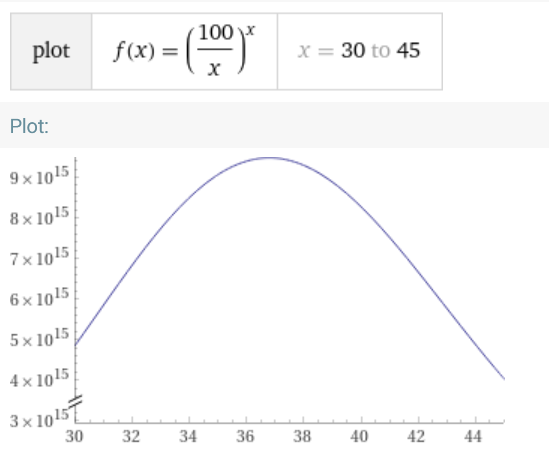
Przybliżenie, dla pewności:

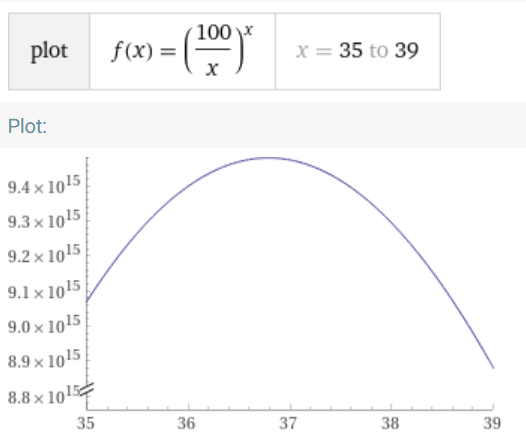
Sprawdźmy jeszcze z ciekawości ile ten maksymalny iloczyn wynosi:

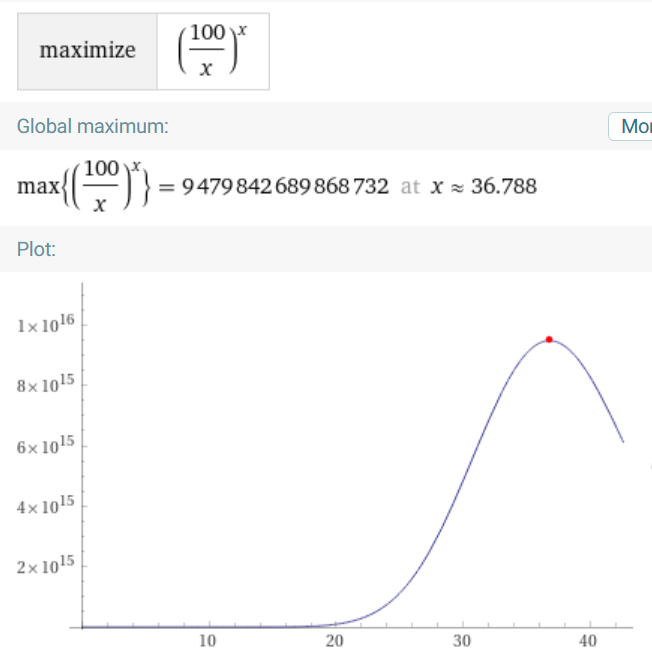
Prawie dziewięć i pół biliarda. Można by to policzyć na piechotę z kartką i ołówkiem, ale zajęłoby kupę czasu...

Zaraz, chwila. Przecież nie da się połamać patyka na 36.788 kawałków 🙂 Sprawdźmy więc iloczyn dla 37:

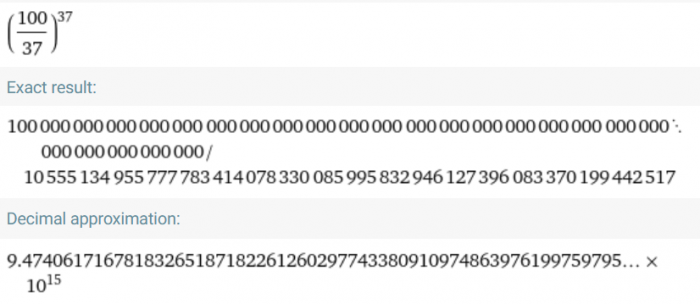
Wyszło odrobinkę mniej, zgodnie z przewidywaniami. Dla świętego spokoju sprawdźmy jeszcze sąsiadów:

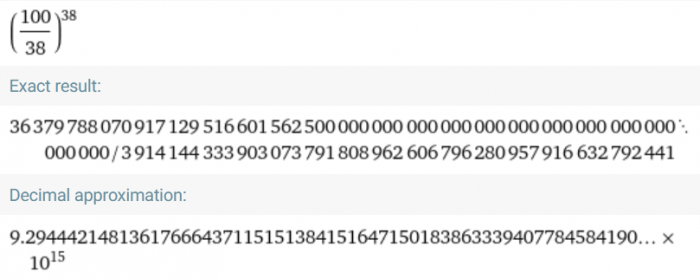
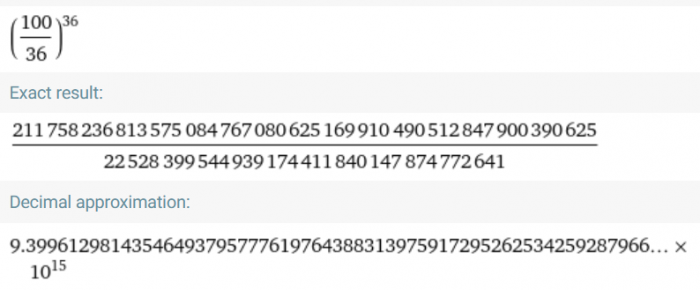
Widzimy, że obydwa "sąsiednie" połamania dają iloczyny mniejsze od tego z 37 kawałkami. Wszystko się zgadza.

A jak Wam poszło?

Wyjątkowo płodnie tym razem! Mamy chyba rekordową ilość nadesłanych rozwiązań. W zagadce wzięli udział wszyscy "starzy" Zagadkowicze a także dwójka nowych.

1Podobnie jak ostatnio, pierwszy odezwał się Rzast. Tym razem jednak niestety nie trafił w poprawne rozwiązanie (ani pierwszej zagadki, ani drugiej). Przypuszczam, że z jakiegoś powodu przyjął, że patyki można łamać wyłącznie na jednakowe kawałki o całkowitej długości, więc wyszło mu pięć kawałków (każdy po 2) w pierwszym pokoju oraz 25 kawałków (każdy po 4) w pokoju drugim. Blisko, ale jednak pudło. Jeżeli kiedykolwiek wrzucę tutaj tą samą zagadkę, ale z dodatkowym ograniczeniem do liczb całkowitych, Rzast ma już kartofla w kieszeni 😉

2Nazajutrz odezwał się Cichy Fragles, który nadesłał poprawne rozwiązanie (i może sobie w związku z tym wyrzeźbić medal z dowolnie wybranego materiału, organicznego lub nie). Cichy pierwszy patyk połamał na piechotę (sprawdzając po kolei poszczególne połamania), a przy drugim najpierw doszedł do postaci (100/n)^n, a potem posłużył się Wolframem.

Najbardziej intrygujący cytat z rozwiązania Cichego to: "Dla patyka o długości 10 można sprawdzić wszystkie możliwości na piechotę". Obstawiam, że jednak nie można 😉 Ale rozwiązanie zaliczam.

3Kilka godzin po Fraglesie rozwiązanie nadesłał Piotr - niestety, liczył na czuja i był blisko, ale jednak niepoprawnie. Pierwszy patyk Piotr połamał na 4 części o długościach 2,3,3,2, z iloczynem 36 (zauważmy, że wynik jest lepszy od wersji Rzasta - i nadal w dziedzinie całkowitej). Drugi - na 40 części. Mógłbym po znajomości zaliczyć w ramach dopuszczalnego marginesu błędu, ale nie zaliczam 🙂

4Tego samego dnia pod wieczór swoje rozwiązanie nadesłał Krzysiek, który - udzieliwszy poprawnych odpowiedzi, okrasił je takim oto komentarzem:

Można udowodnić, że podział musi być na równe części, ale nie chce mi się rozpisywać 🙂 czyli dla podziału patyka na n części iloczyn wynosi (10/n)^n pochodna z tego jest zeruje się w punkcie (10/e) - to nasze maksimum 10/e = 3.6787944117144233 - czyli musimy porównać podział na 3 i 4 części, wygrywa 4. dla 100 - maksimum wynosi (100/e) - porównujemy podział na 36 i 37 równych części. Tu wygrywa 37.

Krzysiek, czerwiec 2021

5Zaraz potem poprawną odpowiedź nadesłał Butter, który najpierw wykumał, że kawałki muszą być równe, a zaraz potem dodał, że rozwiązał obydwa przypadki formułą w Excelu. Chętnie poznam szczegóły formuły!

6Waldek jak zwykle nie zawiódł i nie tylko podał poprawne rozwiązanie, ale też zasugerował, że zagadka byłaby ciekawsza, gdyby ograniczyć długości segmentów do liczb całkowitych (vide: rozwiązania numer 1 i 3 powyżej). Waldek się nie p*lił w jakieś obchodzenie logarytmów dookoła tylko policzył pochodną jak trzeba:

7Jako ostatni, dosłownie na kilka godzin przed zamknięciem zagadki, rozwiązanie nadesłał Rozie, który najpierw zauważył, że długości patyków muszą być większe od jedynki oraz jednakowe, a zaraz potem napisał dwa miniaturowe skrypty w Pythonie, jeden dla 10 a drugi dla 100, które wyrzuciły poprawne rozwiązania. Plus za kreatywne podejście - konstrukcja pętli for gwarantuje, że długość kawałka nie spada poniżej jedynki - bardzo eleganckie.

x = 10 # 100
m = 0
for i in range(1,x):
  s = x / i
  w = s ** i
  if w > m:
    print(i, s, w)
    m = w 

https://xpil.eu/6i7 📋