Zagadka o dwóch identycznych prostokątach "wpisanych" w kwadrat jest o tyle sympatyczna, że nie ma tu podanych żadnych "konkretnych" wymiarów żadnej figury; kwadrat może być długi na dwadzieścia centymetrów lub dwadzieścia parseków.
Wiemy tylko tyle, że obydwa prostokąty mają identyczne wymiary.
Można tu wykonać wiele akrobacji trygonometryczno - planimetrycznych i dojdzie się do wyniku po większych lub mniejszych przebojach. Jeżeli jednak ktoś zauważył, że przekątne obydwu prostokątów są do siebie równoległe...

... to już dalej z górki.
Oznaczmy sobie długość odcinka AE jako x, JD jako y. Ponieważ AE jest taki sam jak BF, a JD - jak FH, oraz ponieważ obydwie przekątne są do siebie równoległe, stąd wniosek że odcinek EJ ma długość x+y.
Odcinek HC również ma długość x+y, bo trójkąty GEJ oraz HCI są identyczne. Czyli bok kwadratu ma długość x+y+x+y czyli 2(x+y).
A skoro obydwa prostokąty są identyczne to odcinek GJ jest tej samej długości co bok kwadratu czyli AB.
Skoro d=x+y a j = 2(x+y), to sinus kąta EGJ wynosi (x+y) / (2(x+y)) czyli 1/2, a więc sam kąt to 30°.
Kąt EGJ jest identyczny z kątem FHG (z podobieństwa trójkątów), a więc ostatecznie odpowiedź to:
30°
Poprawną odpowiedź nadesłało czterech Czytelników, w następującej kolejności: Krzysiek, Futrak, Canthar, Waldek.
Niektóre opisy rozwiązań były całkiem krótkie; jeden z Czytelników rozwiązał zagadkę "intuicyjnie", inny podał prościutki przepis krok po kroku:

... a jeszcze inny - wręcz przeciwnie. Tzn. też krok po kroku, ale dookoła (choć jak najbardziej poprawnie):

Trafił się też jeden wiersz Norwida (ten o gwiazdach) i jedna odpowiedź bazgrana (takie lubię najbardziej, bo mają ten ludzki pierwiastek, którego brakuje bezdusznym pedeefom):

Ogólnie ubawiłem się setnie - doceniam Wasze poczucie humoru!
Fajne rozwiązanie z równoległymi przekątnymi. Problem w tym, że najpierw przydałoby się udowodnić, że rzeczywiście są równoległe, zauważenie „na oko” jest trochę niewystarczające. Może kolejna zagadka: udowodnij, że przekątne są równoległe nie mając wiedzy, że kąt alfa wynosi 30 stopni?
Po pierwsze wiemy, że przekątne są tej samej długości (bo prostokąty są identyczne), po drugie wiemy, że łączą punkty na odcinkach do siebie równoległych (bo kwadrat). To nie wystarczy?
Racja, gupi ja…
Ale przynajmniej szczery 😀
Jako pokłosie Prostej Zagadki Geometrycznej wyniknął mi, ni stąd ni zowąd, intrygujący i chyba trochę ambitniejszy problem. Chodzi oczywiście o dwa zablokowane, czyli bez możliwości ruchu, identyczne prostokąty umieszczone wewnątrz kwadratu o długości boku równej 1.
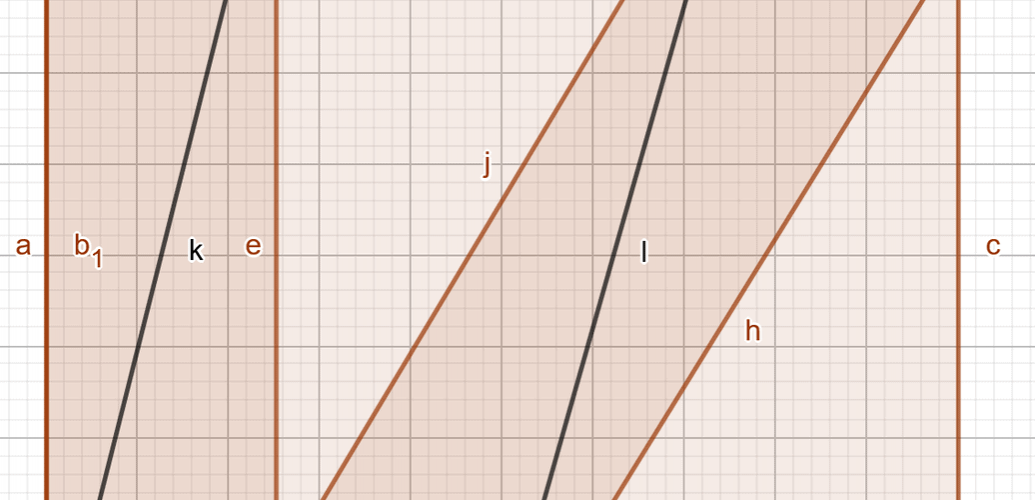
Żeby długo nie tłumaczyć, spójrzcie na rys. 1. To jest pozycja wyjściowa.

Na rys. 2 widać, że żaden ruch tymi prostokątami nie jest możliwy, jeśli żądamy, aby nie miały one punktów wspólnych, za wyjątkiem tych na krawędziach.
Istnieją jednak takie prostokąty, które nie są zblokowane. Można je rozdzielić (obroty + przesunięcia). Tu trzy przykładowe układy wyjściowe (górny rząd) i hipotetyczne sytuacje docelowe (dolny rząd):

~~~~~~~~~~~~~~~~
Pytanie: dla jakich „a” (patrz rys. 1) można te prostokąty rozdzielić?
~~~~~~~~~~~~~~~~~
Wiem, jak to rozwiązać i znam przybliżone rozwiązanie, ale nie znam dokładnej odpowiedzi. Siedzę nad tym już czwartą butelkę wina (i czwarty dzień) i ciągle mylę się gdzieś w rachunkach. Niby proste, same trójkąty, sinusy, cosinusy, Tales…
Gwoli uściślenia, przez „rozdzielić” rozumiemy operację, która „płynnie” przekształci jeden układ prostokątów w drugi wyłącznie za pomocą obrotów i przesunięć w taki sposób, że ani przez chwilę prostokąty nie będą na siebie nachodzić? Nie dopuszczamy „podniesienia” prostokąta poza płaszczyznę i późniejszego „położenia” go z powrotem?
Pięknie to doprecyzowałeś…
Spisałem szczegółowo językiem matematyki wszystkie warunki zadania, ale po krótkim namyśle wyrzuciłem je do kosza. Były zbyt oczywiste, nudne i przyprawiały mnie o mdłości. Są rysunki, więc jak pisał mistrz: Patrz!
Była zagadka, to i wynik powinien być, już dokładny:
a = sqrt 2 * (2-sqrt 3) = 0,378937382…
b = 1/2 *sqrt 2 * (sqrt 3-1) = 0,5176380902…
alfa = pi/12 = 15 stopni
gdzie alfa to kąt, przy którym prostokąty stykają się jedynie narożnikami i są już uwolnione, czyli sytuacja z rys 2., tylko ciut, ciut dalej.
Mam pytanie.
Czy ktoś z szanownych xpil’owiczów próbował podejść do zagadki z rozdzielaniem prostokątów (Waldek 2020/06/21 22:21)?
Po tygodniu zmagań znalazłem rozwiązanie. Jest zaskakująco śliczne (na swój sposób). Niestety, po drodze musiałem wykorzystać wzory dostarczone przez Wolframa, co w znacznym stopniu deprecjonuje sposób uzyskania tego wyniku.
Ponieważ są tu mózgi, które w paru trafnych wzorach potrafią rozkminić to, co mi zajmuje kilka stron skomplikowanych obliczeń, to liczę, że może znajdzie się eleganckie i proste rozwiązanie tego niebanalnego problemu.
Zajmujących się tematem proszę o odzew.