Proszę zapiąć pasy i podkręcić uwagę do samego końca, albowiem dziś (tak dla odmiany) będzie zagadka.
Zagadka brzmi tak:
Spotkało się pięcioro przyjaciół - matematyków i wybrali sobie po pięć liczb całkowitych między 1 a 70.
Zapisali sobie te liczby na karteczkach po czym pokazali sobie nawzajem te karteczki zastanawiając się, co dalej.
Nagle Alicja stwierdziła:
-- O, żadna z wybranych przez nas liczb nie powtarza się!
Na to Bernard:
-- Faktycznie, w dodatku żadne z nas nie wybrało liczby pierwszej!
Celina, po chwili zastanowienia dodała:
-- A zauważyliście, że każda z wybranych przez nas liczb ma co najmniej dwa różne podzielniki pierwsze?
Daniel przyglądał się liczbom długo, potem wyjął kieszonkowy kalkulator i zaczął coś zawzięcie liczyć, wreszcie obwieścił triumfalnie:
-- Nie uwierzycie, ale każdy z nas wybrał liczby, które dają dokładnie ten sam iloczyn!
Edwin zamarł bez słowa. Nic już nie dało się dodać.
Pytanie: ile wynosi iloczyn liczb u każdego z przyjaciół?
Na zachętę powiem jeszcze, że chociaż 5 osób może wybrać po 5 liczb spośród 70 na 4 024 268 454 575 928 378 719 352 903 690 240 (ciut ponad 4 kwintyliardy) sposobów, to zagadkę tę można rozwiązać za pomocą kartki i ołówka, bez komputerów.
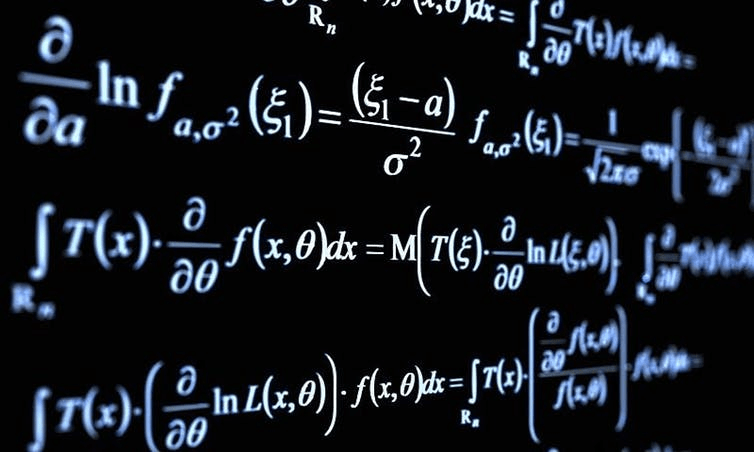
2⁷ * 3⁴ * 5² * 7¹ * 11¹ = 19958400
Ale zaciąłem się na znajdowaniu tych piątek, albo to jest trudne, albo czegoś nie dostrzegam.
Ładnie. Mi to zajęło z pół dnia 🙂 Odpowiedź jak najbardziej poprawna. Co do znajdowania konkretnych układów to najlepiej program sobie napisać, bo na piechotę ciężko. Ale o to już w zadaniu nie pytali.
Nie rozumiem tego zdania – jak ono mogło pomóc:
każdy z nas wybrał liczby, które dają dokładnie ten sam iloczyn!Że co, że jak je wymnoży w dowolnej kolejności to zawsze otrzyma ten sam wynik? A nie wynika to z przemienności mnożenia? A może to ja czegoś nie rozumię…
Każdy z nich wybrał inny zestaw liczb („żadna z wybranych przez nas liczb nie powtarza się”), a mimo to u każdego jest ten sam iloczyn. Pokażę na prostszym przykładzie: dwie osoby, każdy wybiera po dwie liczby. Jeden wybrał (18, 50), a drugi (20, 45). U każdego wychodzi ten sam iloczyn (900), żadna liczba nie powtarza się, każda liczba ma co najmniej dwa różne czynniki pierwsze. Poniatno?
OK, już wiem, źle odczytałem. Każdy matematyk wybrał po pięć liczb, a nie: Każdy matematyk wybrał liczbę (w sumie było ich pięć – a nie 25 jak w treści zadania)