Zagadkę opublikowałem prawie cztery dni temu, niestety jakoś nikomu się nie chciało wziąć z nią za bary.
Ani nawet wziąść, co jest o tyle dziwne, że ludzie na ogół wolą braść niż brać.
Skoro nie ma chętnych, będę niczym ten głos wołającego na puszczy…
A propos ww. puszczy, trochę mnie zdziwiło dlaczego mówi się “na puszczy” a nie “w puszczy”. I wiecie co? Okazuje się, że chodzi o biblijną wersję słowa “pustynia”. Wołający na pustyni.
… na puszczy, powiadam, i sam sobie odpowiem.
Najlepiej będzie zacząć od początku. Uprośćmy sobie naszą zagadkę, czyli – za przeproszeniem – wyekstrahujmy z niej samo gęste.
Numery domów zaczynają się od jedynki i idą sobie w górę, co jeden.
Innymi słowy mamy najzwyklejszy, najbanalniejszy ciąg arytmetyczny o elemencie początkowym równym jeden oraz różnicy równej – dla odmiany – jeden.
O taki: 1, 2, 3, 4, 5, 6, 7, 8,…
Wiemy też, że jeden z wyrazów tego ciągu reprezentuje szukany numer domu (czyli jakieś X):
1, 2, 3, 4, 5, …, X – 1, X, X + 1, X + 2, …
Wiemy też, że ilość domów jest skończona – oznaczmy ją N:
1, 2, 3, 4, … , X – 1, X, X + 1, …, N-1, N.
Ponadto wiemy, że suma numerów domów po lewej stronie X równa jest sumie numerów domów po prawej stronie X:
1 + 2 + 3 + 4 + … + (X – 1) = (X + 1) + (X + 2) + (X + 3) + … + (N – 1) + N
Z podstawówki pamiętamy, że sumę wyrazów ciągu arytmetycznego obliczamy jako:
(A + B) * N * 0.5
gdzie A i B to pierwszy i ostatni wyraz ciągu, a N to ilość jego elementów.
Czyli – najprościej rzecz ujmując – suma wyrazów to średnia arytmetyczna skrajnych wyrazów ciągu przemnożona przez ilość wyrazów ciągu. Logiczne.
Sprawdźmy to sobie na przykładzie:
1, 2, 3, 4, 5
A=1, B=5, N=5. Suma = (1+5) * 5 * 0.5 = 15
Jeszcze jeden przykład:
2, 5, 8, 11, 14, 17
A=2, B=17, N=6. Suma = (2+17) * 6 * 0.5 = 57
Suma numerów domów stojących po lewej stronie od X wynosi więc:
(1 + (X-1)) * (X-1) * 0.5
Suma numerów domów stojących po prawej stronie wynosi:
((X+1) + N) * (N – (X+1) + 1) * 0.5
Układamy równanie:
(1 + (X-1)) * (X-1) * 0.5 = ((X+1) + N) * (N – (X+1) + 1) * 0.5
Upraszczamy:
2 * X^2 = N^2 + N
Ostatnie czego potrzebujemy to znaleźć rozwiązanie powyższego równania w dziedzinie liczb naturalnych, przy ograniczeniu 100 <= X <= 999. Jak tego dokonać?
Ja skorzystałem z Excela. W tym celu wyznaczyłem sobie z powyższego równania X w funkcji N:
X=SQRT((N^2+N)*0.5)
Następnie wygenerowałem sobie w kolumnie A dużo kolejnych wartości N (od stu wzwyż), a w kolumnie B wpisałem formułę:
=SQRT((A2*A2+A2)*0.5)
I skopiowałem ją w dół, daleko.
Następnie przejrzałem wartości w kolumnie B szukając liczby całkowitej.
I co?
I znalazłem, dla N = 288: X = 204.
Tak więc odpowiedzią jest: mieszkam w domu numer 204, a wszystkich domów jest 288.
Inne sposoby na rozwiązanie?
Na przykład za pomocą aplikacji WolframAlpha: początek rozumowania identyczny jak powyżej, z tym, że zamiast rozwiązywać równanie za pomocą Excela, prosimy ładnie Wolframa:
Wchodzimy na stronę https://www.wolframalpha.com
Następnie w polu zapytania wpisujemy:
solve [2*n^2=x^2+x, x>100, x<1000, n>0] over integers
Czyli po naszemu: rozwiąż równanie 2*n^2=x^2+x ograniczając x do wartości między 100 a 1000, przyjmując n dodatnie, na liczbach całkowitych.
Wynik?
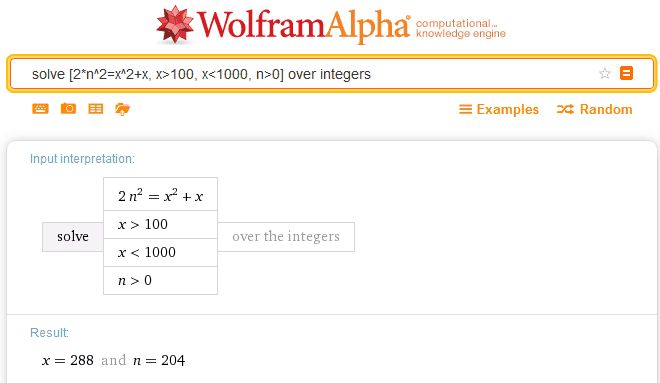
Jak widać wyszło tyle samo, czyli 204 i 288.
Nie mam bladego pojęcia w jaki sposób znaleźć te dwie liczby “na piechotę”, za pomocą samego ołówka i kartki. Może któryś z Czytelników się wypowie…