Zadanie polegało na znalezieniu długości boku N najmniejszego kwadratu N x N, który można idealnie pokryć kafelkami o rozmiarach 3 x 3 oraz 5 x 5, używając co najmniej jednego kafelka każdego rozmiaru.
Jak to ugryźć?
Najpierw zauważamy, że suma pól powierzchni kafli musi się równać polu powierzchni kwadratu. Mniejszy kafelek ma pole powierzchni 3x3=9, a większy 5x5=25:
(1) N2 = 9a + 25b
gdzie a i b to liczby kafli odpowiednio 3x3 i 5x5.
Ponadto zauważamy, że długość boku kwadratu N musi być liczbą, którą da się przedstawić w postaci:
(2) N = 3x + 5y
(gdzie x, y są naturalne)
i to na co najmniej dwa różne sposoby; trójka nie dzieli piątki, więc będą potrzebne co najmniej dwa różne układy trójek i piątek w wierszach kwadratu.
Ponieważ jestem leniwy, poprosiłem Wolframa o znalezienie niskich wartości N, dla których istnieją rozwiązania równości (1) dla naturalnych a, b. Okazuje się, że najmniejsze takie N to 13, potem 14, 16, 17, 18, dalej nie sprawdzałem (zaraz się okaże, dlaczego).
Zobaczmy teraz, czy da się z powyższego wyciągnąć coś więcej. Zaczniemy od najmniejszego znalezionego N, czyli 13.
Dla N=13, a=16 i b=1. Oznacza to, że dysponujemy tylko jednym kaflem 5x5, pozostałe to 3x3. Ale jeden kafel 5x5 pojawi się dokładnie w pięciu wierszach i pięciu kolumnach kwadratu, pozostałe wiersze / kolumny muszą zawierać wyłącznie kafle 3x3, a skoro 13 przez 3 się nie dzieli, to N=13 odpada.
Dla N=14 mamy podobną sytuację: a=19, b=1, czyli tylko jeden kafel 5x5, a 14 się nie dzieli przez 3, czyli odpada.
Dla N=16 mamy a=9, b=7. Musimy więc wpasować 7 dużych kafli w kwadrat 16x16, co oznacza, że co najmniej jeden wiersz (a tak naprawdę co najmniej dwa, ale jeden wystarczy do analizy) będzie zawierał trzy z nich. Trzy kafle 5x5 w jednym wierszu to 15 jednostek, a że cały kwadrat ma bok długi na 16 jednostek, nie pozostaje miejsca na kafelki 3x3. Odpada.
Dla N=17 mamy a=21, b=4. A więc 4 duże kafle 5x5. Co to oznacza? Wszystkie 4 nie zmieszczą się w jednym wierszu, więc pojedynczy wiersz może zawierać 0, 1, 2, albo 3 z nich.
0, 2 i 3 odpadają ze względu na podzielność (a raczej niepodzielność) przez 3:
- 0 odpada bo 17 nie dzieli się przez 3
- 2 odpada, bo jeżeli w wierszu znajdą się dwa kafle 5x5, to pozostało 7 jednostek, a 7 nie dzieli się przez 3
- 3 odpada, bo po wstawieniu 3 kafli 5x5 zostają dwie jednostki, a 2 nie dzieli się przez 3
Zostaje do sprawdzenia 1. Jeżeli w jakimś wierszu będzie jeden kafel 5x5, pozostaje 12 jednostek do wypełnienia kaflami 3x3, co wygląda obiecująco. Pytanie zatem, czy da się ułożyć 4 kafle 5x5 w kwadracie 17x17 tak, żeby w każdym wierszu i każdej kolumnie był dokładnie 1 kafel 5x5?
Nie da się, bo skoro każdy wiersz i każda kolumna zawiera dokładnie 1 kafel 5x5, a łącznie jest takich kafli 4, to musimy zużyć co najmniej 4 wiersze i 4 kolumny, a to oznacza, że potrzebujemy co najmniej 20 jednostek w pionie i tyle samo w poziomie, a kwadrat ma wymiary 17x17. Za krótka kołderka. N=17 odpada.
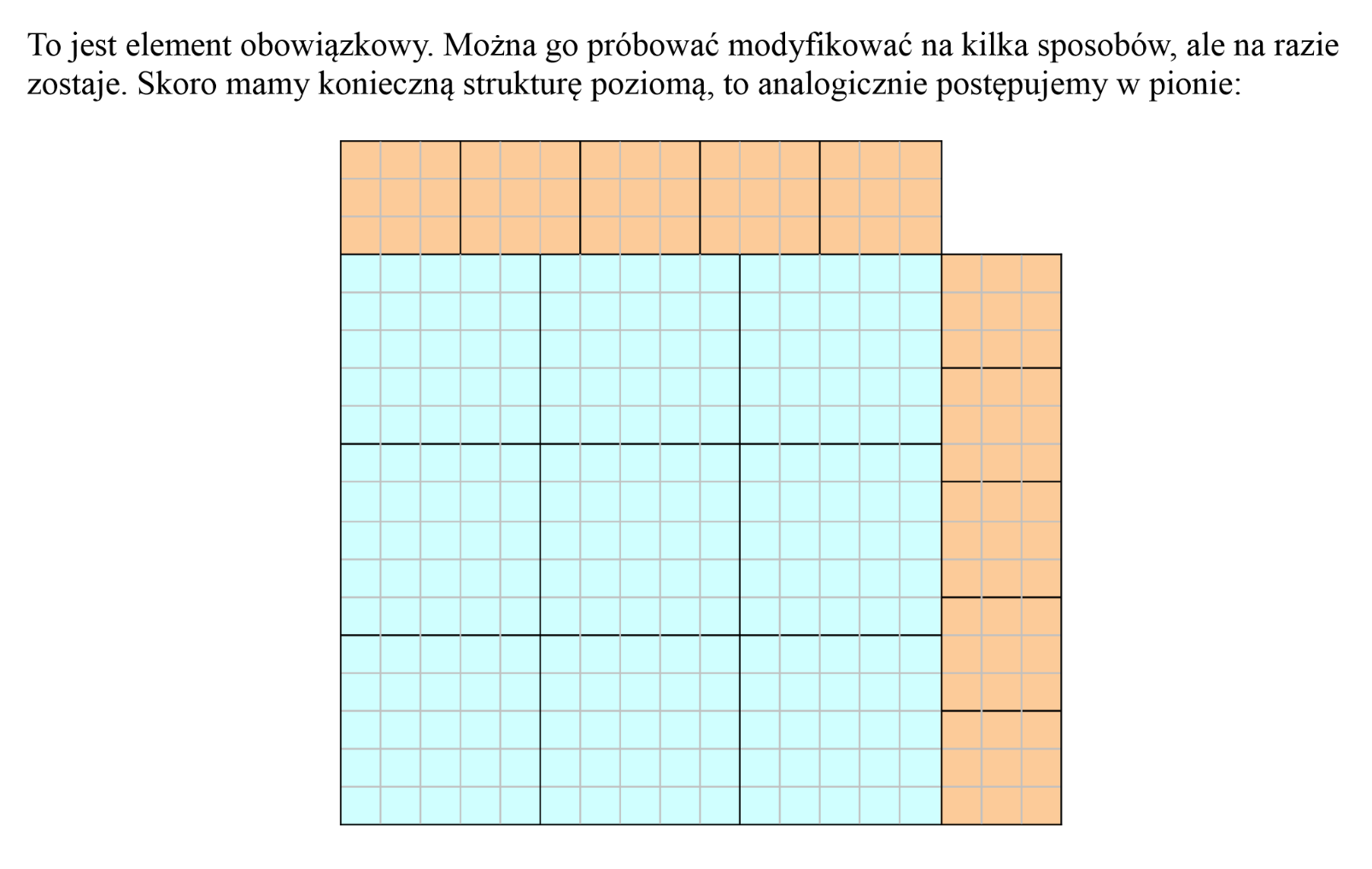
Dochodzimy więc do N=18. I tu pojawia się światełko w tunelu: a=11, b=9. Dziewięć większych kwadratów da się ułożyć w kwadrat 3x3 kafle (czyli 15x15 jednostek), pozostają dwa wąskie pasy o szerokości 3 do wypełnienia kaflami 3x3: pięć w pionie, pięć w poziomie i jeden w narożniku:

Tak więc poprawna odpowiedź to:
N = 18
A jak Wam poszło?
Jeszcze dobrze nie przysechł atrament po publikacji zagadki, a już - w odstępie półtora godziny - przyszły trzy zgłoszenia:
1
Pierwszy był Rozie, który nie tylko podał poprawną odpowiedź, ale też okrasił ją wyjątkowo zwięzłym a celnym komentarzem:
NWW 3 i 5 to 15. Układamy więc kwadrat o boku 15 z 9 sztuk kafli 5x5. Następnie przy prawym i górnym boku kwadratu układamy po 5 kafli 3x3. Dopełniamy na styku kaflem 3x3.
Rozie, piątek wieczór
2
Pół godziny później odezwał się Tacitgreg, który nie tylko podał nieprawidłową odpowiedź (21), ale też uzasadnił ją w sposób tak zawiły, że przeczytawszy ją z dziesięć razy, poddałem się.
3
40 minut później przyszło zgłoszenie Cichego, prawidłowe:
Z dziewięciu kafelków 5x5 układamy kwadrat 15x15, po czym z boku i z góry (albo z boku i z dołu, jak kto woli) dopełniamy go do większego jedenastoma kafelkami 3x3. Mniejszego nie da się zrobić, bo 18 to najmniejsza liczba, którą możemy uzyskać przez dodawanie trójek i piątek na więcej niż jeden sposób (6 * 3 albo (3 * 5) + 3) - nie licząc 15, które można uzyskać z samych trójek lub samych piątek, ale z obu tych liczb już nie.
Cichy, 40 minut później
4
Potem była przez jakiś czas cisza, aż w poniedziałkowy wieczór całkiem elegancką (i w dodatku prawidłową) odpowiedź przysłał Waldek:



Gdzie zachwyty nad moją stroną?
Już były.
Musiałbyś nowy design zapodać…
Przecież jest nowy!
W starej był chyba dodatkowy znacznik br
W starej wersji zdaje się nie było pochyłej czcionki. Zaprawdę, rewolucyjna zmiana 🙂
Po rozwiązaniu jeszcze chwilę się pobawiłem. Można było robić brute force na ilość kwadratów danego typu i sprawdzanie, czy suma ich powierzchni jest kwadratem jakiejś liczby naturalnej. Działa zaskakująco szybko i choć nie daje wprost wyniku, to może mocno pomóc w szukaniu rozwiązania.