Dziś będzie o średnich arytmetycznych w ujęciu nieco innym niż to, do którego większość z nas jest przyzwyczajona.
Przy okazji, jeżeli ktoś jest zainteresowany tematem, pisałem kiedyś o połączeniu średnich arytmetycznej, geometrycznej i harmonicznej, ale nic z tego nie wyszło. Tutaj można poczytać. I trochę też tutaj.
Dziś będzie o kwadratach.
Zaczniemy prościutko: załóżmy, że mamy wylosować odcinek o długości nie przekraczającej jeden. Wszystkie długości są jednakowo prawdopodobne. Ile wylosujemy?
Nie wiadomo. Możemy wylosować 0.001203 albo 0.9995354 albo 0.387634 albo 0.8774837465 albo nawet 0.28364758784.
Spróbujmy więc wykoncypować co się stanie, jak zaczniemy losować takie odcinki w ilościach hurtowych. Jakiej ŚREDNIEJ długości odcinka możemy się spodziewać?
Intuicja podpowiada, że 0.5. I ma rację, skubana, bo faktycznie losując dużą ilość liczb z przedziału 0-1 dostaniemy średnią w okolicy 0.5.
No dobra. Mamy więc pierdylion odcinków o różnych długościach z przedziału 0-1.
Teraz - uwaga - bierzemy każdy z nich i budujemy z niego kwadrat o boku równym długości tego odcinka.
W efekcie mamy teraz pierdylion kwadratów większych i mniejszych. Każdy z nich ma uczciwie wylosowaną długość boku z przedziału 0-1.
Ile wynosi średnia oczekiwana powierzchnia takiego kwadratu?
myślu, myślu, myślu... średnia długość odcinka to połowa, podniesione do kwadratu da nam... ćwiartkę! A więc odpowiedź brzmi 0.25. Proste...
Prawda. Z tym, że - jak to często bywa na tym blogu - gówno prawda 😉
Skąd wiemy, że 0.25 to odpowiedź błędna?
Zaczniemy od prostej symulacji. Na przykład w Excelu: W kolumnie A wstawiamy 10,000 razy formułę =RAND(), w kolumnie B podnosimy ją do kwadratu:
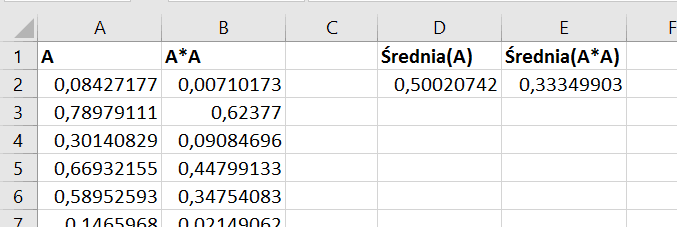
Widzimy, że o ile średnia długość odcinka zachowuje się poprawnie i oscyluje w okolicach połówki, o tyle już jej kwadrat olał zupełnie naszą zbolałą intuicję i bezczelnie próbuje wylądować w okolicach jednej trzeciej.
No ale nie należy ufać Microsoftowi, prawda? Może spróbujmy jakoś inaczej to sprawdzić? Może w Pythonie?
from random import random
N = 1000000
print( sum([random()**2 for _ in range(N)] )/N )
Wynik: 0.33332485400893097
Noż kurdę. Jednak nie kłamali w tych Excelach, faktycznie wychodzi 1/3. Ale dlaczego?
Na chłopski rozum dlatego, że kwadrat jest funkcją wklęsłą. A funkcje wklęsłe zyskują na różnorodności. Czym bardziej wylosowana długość boku kwadratu będzie się różnić od wartości oczekiwanej (1/2), tym "bardziej do kwadratu" będzie się różnić powierzchnia kwadratu.
Jeszcze bardziej na chłopski rozum: podzielmy nasz kwadrat 1x1 na dwa kawałki: jeden kawałek to kwadrat 0.5 x 0.5 zbudowany z punktów należących do wszystkich kwadratów opartych na odcinku krótszym niż 0.5, a drugi to figura w kształcie litery L złożona z trzech takich kwadratów 0.5 x 0.5, reprezentująca wszystkie punkty należące do kwadratów o długościach boków większych od 0.5, a nienależące do tego pierwszego kwadratu 0.5 x 0.5. Mamy jeden - do - trzech.
A teraz wyjaśnienie, za przeproszeniem, analityczne (nawiasem mówiąc słowo "analityczka" jest dość niefortunne leksykalnie, jeżeli odpowiednio nieuważnie wstawi się doń spacje). Otóż gęstość funkcji prawdopodobieństwa długości odcinka wynosi \(\int_0^1 x dx\) czyli dokładnie 0.5.
Natomiast gęstość analogicznej funkcji w przypadku kwadratu to już \(\int_0^1 x^2 dx\) czyli 1/3 (dlaczego? Szukamy funkcji, której pochodna daje \(x^2\), jest nią \(\frac{1}{3}x^3\), po podstawieniu za x granic całkowania i odjęciu wychodzi dokładnie 1/3).
Tak to właśnie intuicja zwodzi nasze gruczoły matematyczne. Pół biedy, jeżeli czytamy o tym na jakimś bogu ducha winnym, zapyziałym blogu - gorzej, jeżeli taka całka ugryzie nas w kontekście, na ten przykład, rynku nieruchomości.
Albowiem w przypadku kredytów mieszkaniowych mamy do czynienia z funkcją wypukłą (zamiast omawianej wcześniej funkcji wklęsłej).
Jak to działa?
Załóżmy, że w "normalnych" warunkach średnio 95% pożyczkobiorców spłaca swoje kredyty w terminie. 5% natomiast ma kłopoty finansowe i pomimo stabilnego rynku nieruchomości nie jest w stanie spłacać kredytu. To zwyczajny bieg rzeczy - 95% płaci, 5% traci swoje nieruchomości bo nie stać ich na spłatę. Kółko się toczy.
Z tym, że jeżeli tylko ceny nieruchomości zaczną iść w dół (nawet nieznacznie), odsetek ludzi, którzy przestaną spłacać kredyty - wzrośnie. Ponieważ część z nich podejmie (raczej słuszną) decyzję, że nie warto spłacać milionowego kredytu za chałupę wartą 980,000 - lepiej wysłać jingle mail do banku i wyjść na zero, niż spłacić cały kredyt i wyjść na minus.
A dlaczego mówimy o funkcji wypukłej a nie liniowej?
Ponieważ proporcja między ilością kredytów spłacanych a niespłacanych w warunkach stabilnych wynosi 95:5 - bardzo niewiele da się zrobić, żeby zmniejszyć te 5% (nie zmniejszymy tej wartości bardziej niż do 0%, choćbyśmy się zesrali), natomiast jest mnóstwo miejsca, żeby te 5% zwiększyć. Właśnie ta asymetria sprawia, że funkcja zysków banków względem średnich cen nieruchomości jest funkcją wypukłą. I dlatego banki tracą nie tylko na spadku cen średnich, ale też na różnorodności cen między różnymi rejonami kraju (w tym drugim przypadku zależność jest trochę bardziej skomplikowana, ale ogólna zasada pozostaje).
Całe szczęście, że się na tym wszystkim nie znam - wszystkie mądrości z dzisiejszego wpisu znalazłem na jednym z moich ulubionych blogów: !klik!
Nic z tego nie rozumiem i nie chce rozumieć, ale czytam właśnie kapitalna, dobrze napisana książkę, na wdechu, o geniuszach matematycznych.
Znasz może? ”Genialni LWOWSKA SZKOŁA MATEMATYCZNA” Mariusza Urbanka. Faktycznie, książka zaczyna się we Lwowie, ale opisuje burzliwe życie i kariery wszystkich najwspanialszych matematyków polskich zahaczając o światowych w dwudziestoleciu międzywojennym. Dowiesz się na przykład jak Ulam został współtwórcą bomby atomowej w Los Alamos u Oppenheimer-a
Namiar na książkę zanotowany, przy najbliższej okazji zapoluję. Dziękować! A o Ulamie (i innych matematykach) często tu pisuję, mocarze to byli, zaiste.