Rozwiązanie zagadki o czarodziejskich kamykach

https://xpil.eu/9pu 📋

Postawiona niedawno zagadka o ulepszaniu czarodziejskiej zbroi magicznymi kamykami...

...a może na odwrót, tj. magicznej zbroi czarodziejskimi kamykami? hmmm...

...jest całkiem prosta jak się zna metodę, a metodę się zna na podstawie kaczuszek - wystarczy regularnie czytać mój blog i wszystko jasne.

Pogubione kaczuszki: rozwiązanie zagadki

Podobnie jak w przypadku zagadki o kaczkach, tu też mamy do czynienia z pochłaniającym procesem Markowa. ("Pochłaniającym", bo z końcowego stanu już się nie wychodzi).

Macierz przekształceń prezentuje się tu nader prosto:

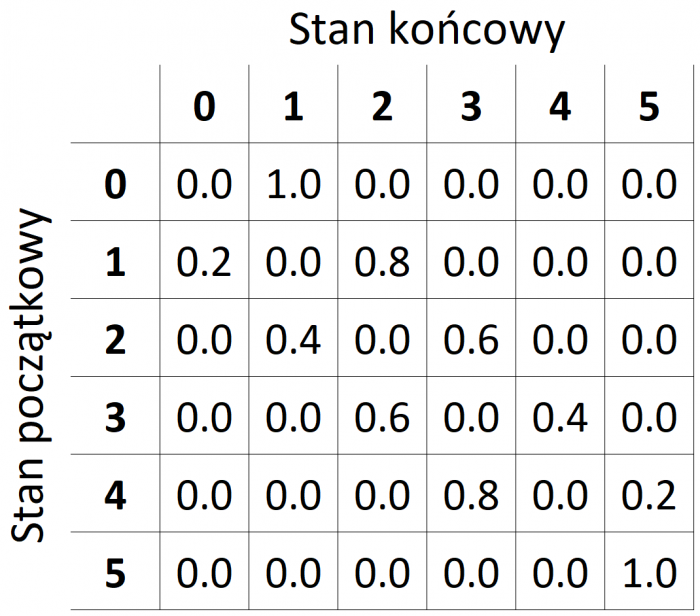
Zgodnie z teorią, należy teraz zbudować macierz fundamentalną. Banalna sprawa: bierzemy powyższą macierz i obcinamy z niej ostatni wiersz i ostatnią kolumnę, a to co zostało odejmujemy od macierzy jednostkowej 5x5 (czyli złożonej z samych zer z wyjątkiem jedynek na głównej przekątnej).

Wynik odwracamy i mnożymy przez kolumnę jedynek:

Wynik powyższego to:

Oznacza to, że z poziomu zero do piątki dotrzemy średnio po zużyciu ~42.6667 kamyków. Dla zaokrąglenia 43.

Tak naprawdę nawet gdyby w wyniku wyszło trochę mniej niż 42.5, i tak wynikiem byłoby 43, bo startując od zera nieparzyste poziomy uzyskujemy wyłącznie po nieparzystej liczbie kroków. Ale wyszło ~42.6667 więc spoko.

Symulacja procesu jest trywialna i potwierdza powyższy wynik:

from random import random
kroki = 0
for próby in range(1000000):
    poziom = 0
    while poziom < 5:
        poziom += 1 if random() < 1-(poziom*.2) else -1
        kroki += 1
print(kroki/próby)

Wynik wychodzi zawsze w okolicach 42.6, czyli wszystko się zgadza.

Można też proces zasymulować z innego punktu widzenia: sprawdzić ile razy uda się dojść z poziomu 0 do poziomu 5 przy zadanej liczbie posiadanych kamyków:

from random import random

for ilekamykow in range(5, 300, 2):
    sukcesy, porażki = 0, 0
    for n in range(1000):
        kamyki = ilekamykow
        kroki, poziom = 0, 0
        while poziom < 5 and kamyki > 0:
            poziom += 1 if random() < 1-(poziom*.2) else -1
            kamyki -= 1
        if poziom == 5:
            sukcesy += 1
        else:
            porażki += 1
    print(ilekamykow, sukcesy, porażki)

kamyki sukcesy porażki
5 50 950 
7 66 934 
9 138 862
11 156 844
13 195 805
15 271 729
17 304 696
19 341 659
21 338 662
23 397 603
25 437 563
27 455 545
29 506 494
31 502 498
33 541 459
35 550 450
37 594 406
39 602 398
41 658 342
43 642 358
45 655 345
47 662 338
49 716 284
51 707 293
53 736 264
55 771 229
57 741 259
59 766 234
61 790 210
63 792 208
65 787 213
67 820 180
69 815 185
71 825 175
73 821 179
75 872 128
77 857 143
79 866 134
81 878 122
83 873 127
85 876 124
87 904 96
89 894 106
91 899 101
93 912 88
95 926 74
97 930 70
99 912 88
101 932 68
103 947 53
105 929 71
107 920 80
109 937 63
111 943 57
113 948 52
115 933 67
117 931 69
119 954 46
121 955 45
123 960 40
125 965 35
127 958 42
129 949 51
131 967 33
133 970 30
135 962 38
137 965 35
139 969 31
141 971 29
143 972 28
145 961 39
147 982 18
149 985 15
151 973 27
153 977 23
155 981 19
157 977 23
159 986 14
161 987 13
163 988 12
165 981 19
167 992 8
169 987 13
171 994 6
173 991 9
175 991 9
177 990 10
179 995 5
181 995 5
183 996 4
185 991 9
187 992 8
189 990 10
191 995 5
193 990 10
195 998 2
197 991 9
199 990 10
201 997 3
203 992 8
205 993 7
207 997 3
209 996 4
211 993 7
213 999 1
215 997 3
217 995 5
219 999 1
221 996 4
223 995 5
225 999 1
227 996 4
229 998 2
231 998 2
233 995 5
235 999 1
237 998 2
239 998 2
241 999 1
243 999 1
245 998 2
247 999 1
249 1000 0
251 998 2
253 998 2
255 999 1
257 1000 0
259 999 1
261 999 1
263 999 1
265 997 3
267 1000 0
269 1000 0
271 999 1
273 999 1
275 1000 0
277 1000 0
279 998 2
281 997 3
283 1000 0
285 999 1
287 1000 0
289 999 1
291 1000 0
293 1000 0
295 1000 0
297 1000 0
299 1000 0

Jak widać przy małej liczbie kamyków sukcesy są rzadkością - potrzeba około 21 kamyków żeby osiągnąć sukces w 33% prób oraz gdzieś między 27 a 29 żeby było fifty-fifty. Biorąc pod uwagę bardzo długi ogon tego rozkładu łatwo uwierzyć, że wartość oczekiwana faktycznie ląduje w okolicach 43 kamyków.

Jak długi konkretnie? Sprawdźmy dla 100 tysięcy prób:

from random import random
from matplotlib import pyplot as plt

wyniki = []
makskroki = 0
for n in range(100000):
    kroki, poziom = 0, 0
    while poziom < 5:
        poziom += 1 if random() < 1-(poziom*.2) else -1
        kroki += 1
    if kroki > makskroki:
        makskroki = kroki
    wyniki.append(kroki)
print(makskroki)
plt.hist(wyniki, bins=makskroki)
plt.show()

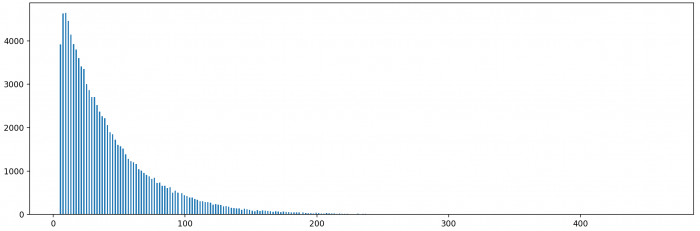
A jak Wam poszło?

Intrygująco! Wygląda na to, że gdzieś po drodze nastąpiło iskrzenie na łączach...

1Zaczęło się od Waldka, który znalazł lokalne maksimum równe 9 i takiej też udzielił odpowiedzi. W dodatku udało mu się poprzeć tę odpowiedź symulacją w Excelu, z której wynika, że prawdopodobieństwo rośnie od 5 do 7 kroków, i od 7 do 9, a potem już tylko maleje. Co ciekawsze, Waldek przeprowadził również obliczenie na macierzach (i nawet odwołał się do Markowa), ale jego wzory nie wyglądają mi za dobrze - macierz Waldka jest 6x6 a powinna być 5x5. Zasadniczo Waldek znalazł maksimum histogramu (tego samego, który udało mi sie narysować powyżej), ale to przecież nie to samo co oczekiwana liczba kamyków potrzebnych do osiągnięcia 5 poziomu. Nie zaliczam.

2Drugi był Butter, który napisał dość rozległy skrypt symulujący proces w Pythonie i mu wyszło 7. Niestety, skrypt się był rozjechał w transmisji (wsiorbało mu wcięcia linii), a że nie chciało mi się tego na miejscu korygować, to nie wiem gdzie Butter popełnił błąd - przypuszczam, że jego rozumowanie było analogiczne do waldkowego, bo na histogramie wartości dla siódemki i dziewiątki są bardzo zbliżone. W każdym razie nie zaliczam.

3Podobnie jak przy poprzedniej zagadce, tutaj Waldek znów się przespał z problemem i nazajutrz nadesłał kolejne rozwiązanie. Już się ucieszyłem, a tu jednak okazało się, że to tylko korekta kilku literówek z poprzedniego rozwiązania. Dużo tabelek i obliczeń z wynikiem 9. Nadal nie zaliczam.

4 Czwarty był Rozie i jemu symulacja w Pythonie też pokazała dziewiątkę (po stu milionach prób!). Ewidentnie się tym razem nie dogadaliśmy z Czytelnikami. Zwykle w takich sytuacjach winię szarą substancję między uszami rozwiązujących, ale to już trzecia osoba, która wysyła rozwiązanie oparte na maksymalnym słupku w histogramie zamiast szukać oczekiwanej liczby kamyków. Gdzie popełniłem błąd?

Tym razem to ja przespałem się z problemem i okazało się, że faktycznie walnąłem subtelnego, ale istotnego babola. Otóż w treści oryginalnej zagadki było pytanie o najbardziej prawdopodobną liczbę magicznych kamyków potrzebnych do osiągnięcia piątego poziomu, tymczasem na myśli miałem wartość oczekiwaną.

We wtorek po południu odwiesiłem więc aureolę na kołek, skorygowałem treść zagadki i rozesłałem wieści do Waldka, Buttera i Roziego. Postanowiłem też przesunąć termin publikacji rozwiązania o kilka dni do przodu, żeby dać ludkom szansę na ewentualne poprawki tudzież korekty.

5Nazajutrz rozwiązanie nadesłał Krzysiek. Piękne rozwiązanie, muszę przyznać. Najpierw rozwiązał zadanie układem pięciu równań z pięcioma niewiadomymi, a potem jeszcze napisał symulację w Pythonie. Co prawda kod mi się rozjechał, więc go tu nie zaprezentuję, ale proszę zerknąć na rozwiązanie algebraiczne:

6Nie zdążyły jeszcze porządnie wybrzmieć fanfary po rozwiązaniu Krzyśka, a tu bocznym kanałem (Telegram) nadeszła kolejna odpowiedź Buttera. Niestety błędna, acz o włos od poprawnej. Z symulacji w Pythonie Butterowi wyszło 41. Uruchomiłem jego kod na swojej lokalnej maszynie - faktycznie, 41 jak w mordę strzelił. Nie chciało mi się już analizować gdzie tkwi błąd - oto kod Buttera, może komuś się akurat nudzi:

from random import choices, seed
import time

seed(time.time())
wagi = [[10,0], [8,2], [6,4], [4,6], [2,8] ]

def spr():
    level = 0
    kroki = 0
    while (level<5) or (kroki>10000):
        waga  = wagi[level]
        kroki +=1
        wynik = choices(['G','D'],waga)
        if wynik[0] == 'G':
            level +=1
        elif level>1:
            level -=1
    return kroki    
        
wynik = {}
ile  = 1000000
for x in range(ile):
    kr = spr()
    try:
        wynik[kr] += 1
    except:    
        wynik[kr] = 1        

exp = 0
for k,v in wynik.items():
    exp += (k*v)

print(exp/ile)

7Dzień później poprawione rozwiązanie przysłał Rozie - rzecz jasna zaliczam.

8Przyszło też zgłoszenie od Tywana, poprawne. Również oparte na układzie równań. Zaliczam.

Podsumowując, w zasadzie powinienem przyznać medal Waldkowi, który jako pierwszy nadesłał poprawne rozwiązanie oryginalnie sformułowanej zagadki. Ale że to mój blog i mogę tu sobie posadzić dziada z babą i gówno mi kto zrobi 🙂 tym razem przyznaję dwa równorzędne medale: jeden Waldkowi, bo był pierwszy; drugi Krzyśkowi, bo był pierwszy przy poprawionej wersji, a w dodatku znalazł rozwiązanie, na które sam nie wpadłem. Solidna robota, panowie.

A sam - w ramach autopokuty - sypię sobie na łeb wiaderko popiołu. Muszę bardziej uważać następnym razem.

https://xpil.eu/9pu 📋