Bierzemy liczbę, dajmy na to, 113.
Jest pierwsza?
No jest.
Obcinamy jedną cyfrę od lewej, zostaje 13.
Też pierwsza.
Odcinamy kolejną cyfrę od lewej, zostaje 3.
Też pierwsza!
A są dłuższe takie liczby?
Najmniejsza czterocyfrowa to 1223, ponieważ zarówno 223 jak i 23 oraz 3 są pierwsze. Największa - 9967
A pięciocyfrowe?
A dziesięcio-?
Okazuje się, że wszystkich takich liczb jest dokładnie 4260, z czego największa ma aż dwadzieścia cztery cyfry:
357686312646216567629137
... i jest jedyną liczbą 24-cyfrową o tej własności.
A skąd wiadomo, że nie ma większych?
Wystarczy dopisać na początku (tj. z lewej strony) każdą z cyfr 1-9 i sprawdzić, że żadna z powstałych w ten sposób liczb nie jest pierwsza.
Nudne, prawda?
No to żeby na koniec trochę unienudnić, poniżej prezentuję grafy utworzone z takich właśnie liczb, ale tylko do pięciocyfrowych (większy graf wygląda już dość nieczytelnie):
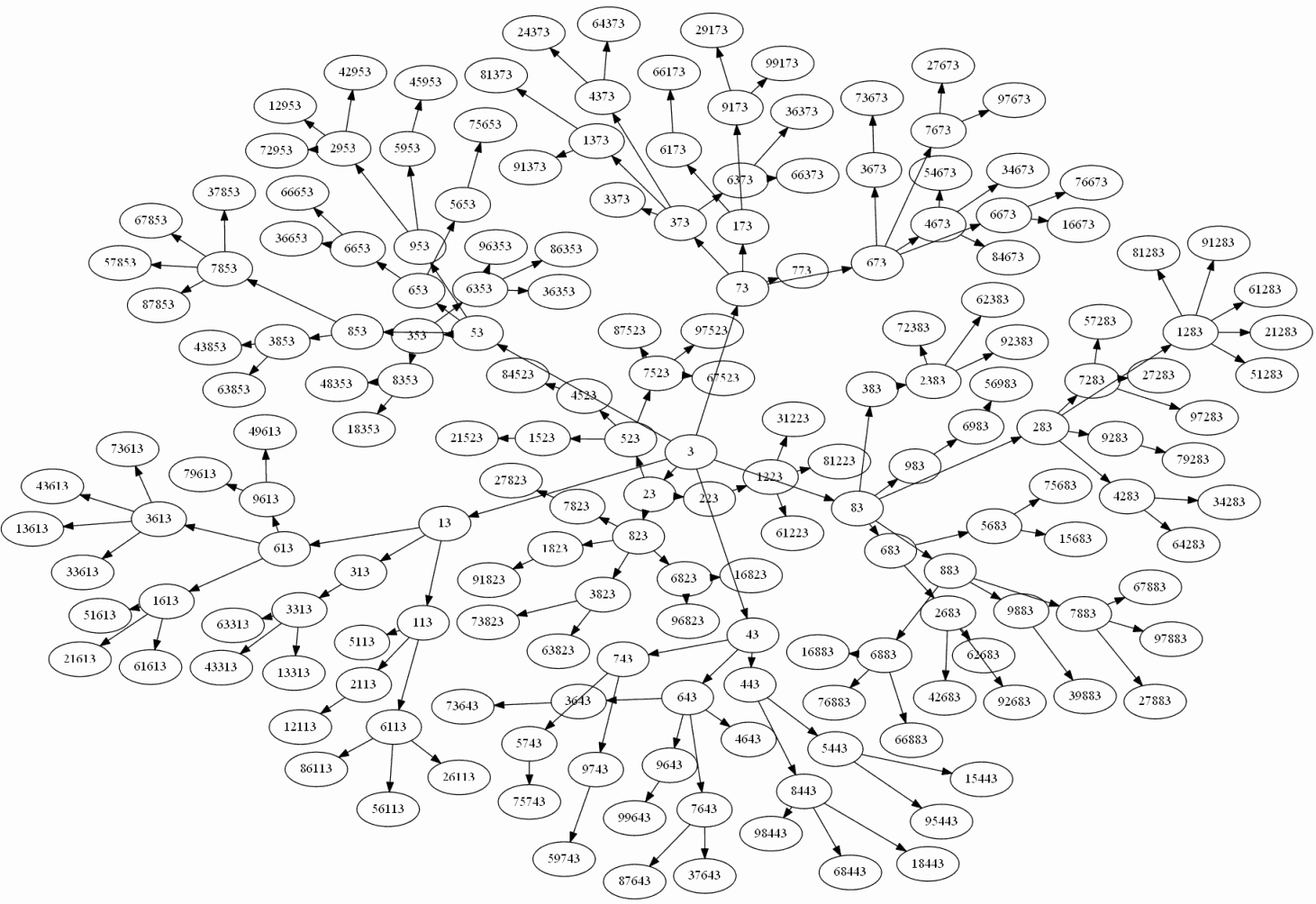
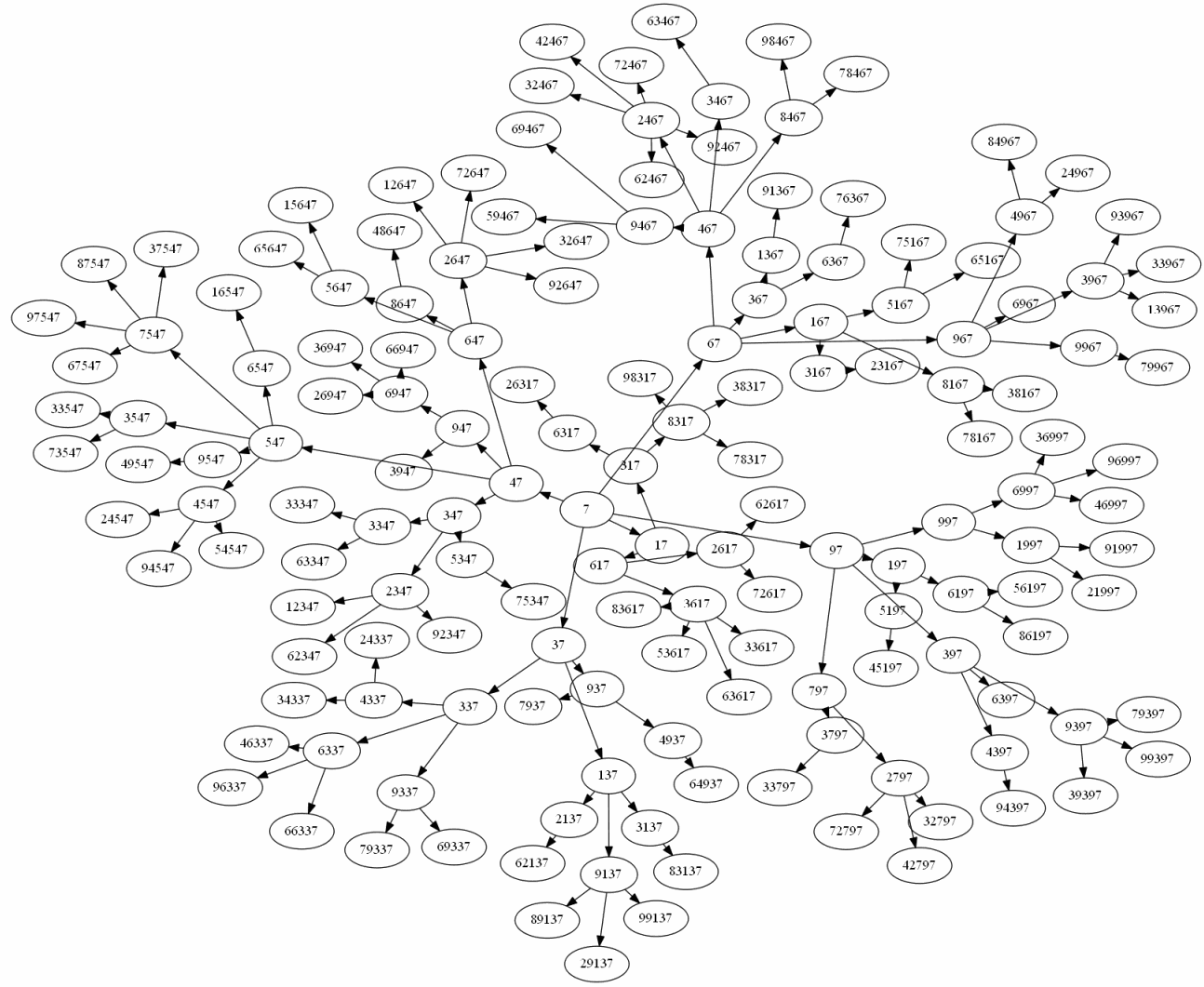
Dwójkę i piątkę pominąłem jako mało interesujące.
czym robiłeś grafy?
GraphViz