W zagadce chodziło o to, żeby ustalić jakie jest prawdopodobieństwo, że wyrzucimy trzema monetami tyle samo orłów, ile wypadnie nam jedynek lub szóstek na trzech kostkach oraz tyle samo, ile kierów pojawi się na trzech losowo wybranych kartach ze standardowej talii.
Możliwe liczby uzyskane w każdym z tych trzech doświadczeń to 0, 1, 2 lub 3. Mamy więc cztery warianty do policzenia. Spróbujmy jednak najpierw chociaż zgrubnie oszacować czego właściwie powinniśmy oczekiwać. Oto prosty kod z symulacją:
from random import random, sample print(100*round(len([1 for n in range(10000000) if len([1 for n in range(3) if random() < 1/2]) == len([1 for n in range(3) if not(1/6 < random() < 5/6)]) == len([1 for n in sample([x for x in range(52)], k=3) if n < 13])])/10000000, 5), "%")
Żartuję. Poniżej to samo, tylko bardziej czytelnie 🙂
from random import random, sample
def monety():
return len([1 for n in range(3) if random() < 1/2])
def kosci():
return len([1 for n in range(3) if not(1/6 < random() < 5/6)])
talia = [x for x in range(52)]
def karty():
return len([1 for n in sample(talia, k=3) if n < 13])
proby = 10000000
wynik = len([1 for n in range(proby) if monety() == kosci() == karty()])
print(100*round(wynik/proby, 5), "%")
W wyniku dostaję zawsze liczbę w okolicach 9.95 - wiemy więc pi x drzwi czego się spodziewać. Spróbujmy teraz policzyć to bez używania symulacji.
Przyjmę oznaczenia X, Y, Z odpowiednio dla monet, kości i kart.
Prawdopodobieństwa oznaczę P{X|Y|Z}{0|1|2|3}. Przykładowo PY2 to prawdopodobieństwo uzyskania dokładnie dwóch kostek z jedynką lub szóstką, a PZ0 to prawdopodobieństwo, że nie wylosujemy ani jednej karty w kolorze kier.
Plan jest taki, żeby policzyć PX0, PX1, PX2, PY0 i tak dalej aż do PZ3, potem wyznaczyć P0 jako PX0*PY0*PZ0, P1 jako PX1*PY1*PZ1 i tak dalej, wreszcie ustalić końcowe prawdopodobieństwo P jako sumę P0 do P3.
Graficznie można to przedstawić mniej więcej tak:
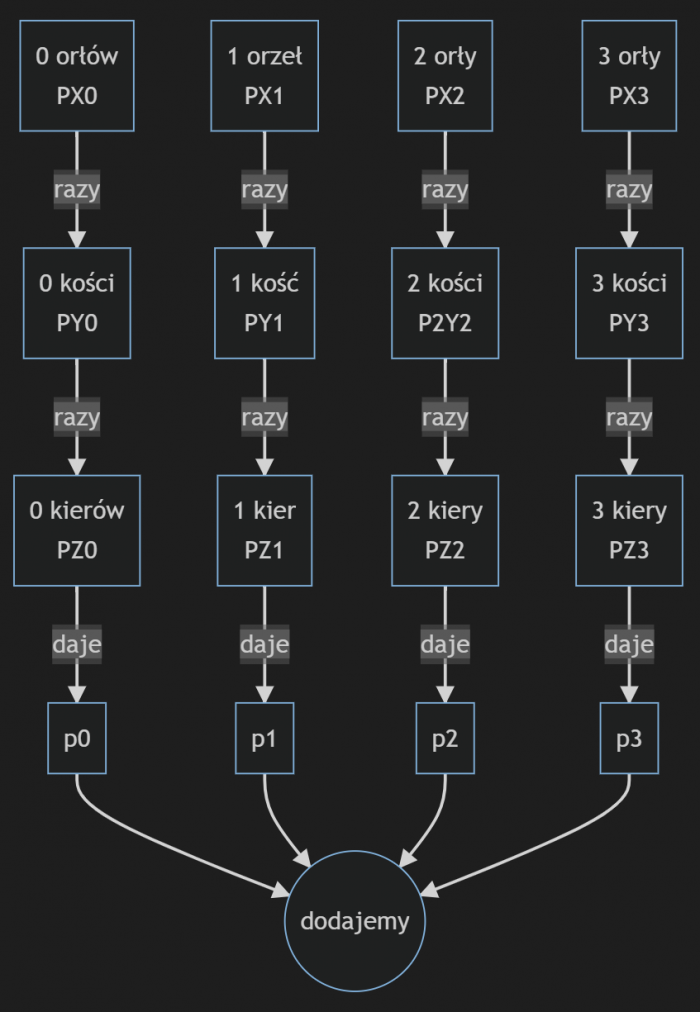
No to zaczynamy.
Najpierw monety, bo są najłatwiejsze:
PX0 = 1/8 (RRR)
PX1 = 3/8 (ORR, ROR, RRO)
PX2 = 3/8 (OOR, ORO, ROO)
PX3 = 1/8 (RRR)
Kości:
PY0 = 2/3 * 2/3 * 2/3 = 8/27
PY1 = 3 * 1/3 * 2/3 * 2/3 (mnożymy przez 3 bo "dobra" kość może pojawić się na pierwszej, drugiej lub trzeciej pozycji)
PY2 = 3 * 1/3 * 1/3 * 2/3
PY3 = 1/3 * 1/3 * 1/3 = 1/27
Karty (najwięcej kombinowania):
PZ0 = 39/52 * 38/51 * 37/50 = 703/1700 (losujemy nie-kiera trzy razy - najpierw mamy 39 pasujących kart wśród 52, potem 38 w 51 itd)
PZ1 = 3 * 13/52 * 39/51 * 38/50 = 741/1700 (jeden kier spośród 13 kierów, i potem dwa nie-kiery spośród pozostałych, a mnożymy przez trzy bo kier może pojawić się pierwszy, drugi lub trzeci)
PZ2 = 3 * 13/52 * 12/51 * 39/50 = 117/850
PZ3 = 13/52 * 12/51 * 11/50 = 11/850
Na wszelki wypadek sprawdzamy czy PZ sumują się do jedynki: 703/1700 + 741/1700 + 117/850 + 11/850 = 1
Teraz trzeba policzyć P0, P1, P2 i P3:
P0 = PX0 * PY0 * PZ0 = 1/8 * 8/27 * 703/1700 = 703/45900
P1 = PX1 * PY1 * PZ1 = 3/8 * 4/9 * 741/1700 = 247/3400
P2 = PX2 * PY2 * PZ2 = 3/8 * 2/9 * 117/850 = 39/3400
P3 = PX3 * PY3 * PZ3 = 1/8 * 1/27 * 11/850 = 11/183600
I je dodać:
P0 + P1 + P2 + P3 = 703/45900 + 247/3400 + 39/3400 + 11/183600 = 6089/61200 ≈ 0.09949346
Tak więc poprawna odpowiedź brzmi 9.9% i zgadza się ona pi x drzwi z symulacją.
A jak Wam poszło?
1Jako pierwszy odezwał się tym razem Butter, który - podobnie jak ostatnim razem - napisał symulator w Pythonie i po milionie prób wyszło mu 9.9%. Zaliczam.
Poniżej kod Buttera - jak widać logika identyczna jak u mnie, tylko więcej szczegółów przy talii kart. Mi się nie chciało bawić w kolorki i uznałem, że lista 0..51 wystarczy (kiery 0..12, wszystko powyżej to nie-kiery), a Butter ładnie porozbijał na poszczególne kolory.
from random import randint, shuffle, sample
from itertools import product
from collections import Counter
num_coins = 3
def getCoins():
coins = [randint(0, 1) for r in range(num_coins)] # 1 = orzeł
count = 0
for pos in coins:
count += pos
return count
def getDices():
dices = [randint(1, 6) for r in range(num_coins)]
count = 0
for pos in dices:
if pos in (1, 6):
count += 1
return count
suits = ["s", "d", "h", "c"]
values = ["1", "2", "3", "4", "5", "6", "7", "8", "9", "10", "11", "12", "13"]
deck = list(product(values, suits))
def getCards():
shuffle(deck)
hand = sample(deck, num_coins)
count = 0
for pos in [card[1] for card in hand]:
if pos == 'h':
count += 1
return count
ile_razy = 1000000
trafienia = 0
for x in range(ile_razy):
coins = getCoins()
dices = getDices()
cards = getCards()
if coins == dices == cards:
trafienia += 1
wynik = trafienia / ile_razy
print('{0:.4%}'.format(wynik))
2Potem nadeszło zgłoszenie Waldka, który potraktował zagadkę teoretycznie i też mu wyszło 9.9%. Zaliczam.
Prawdopodobieństwa dla:
Monety 3:1/8, 2:3/8, 1:3/8, 0:1/8
Kostki 3:1/27, 2:6/27, 1:12/27, 0:8/27
Talia 3:0,0129, 2:0,1376, 1:0,4359, 0:0,4135
Teraz trzeba wymnożyć prawdopodobieństwa od tych samych cyferek, otrzymane iloczyny dodać i już.
(C) Waldek, marzec 2022
3Trzeci był Rozie, który najpierw wykonał doświadczenie (znów Monte Carlo), ale wyszło mu że 9.95% czyli na dwoje babka wróżyła, więc policzył też porządnie i dostał ~9.949%, czyli w zaokrągleniu 9.9%, czyli zaliczam.
Kod Roziego poniżej. Ciekawe, że też zastosował 10 milionów powtórzeń głównej pętli.
import random
card = [0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,3,3,3,3,3,3,3,3,3,3,3,3,3]
tries = 10000000
equal_c = 0
for i in range(0, tries):
coin_c = 0
dice_c = 0
card_c = 0
for i in range(0, 3):
tmp = random.randint(0, 1)
if tmp == 0:
coin_c += 1
for i in range(0, 3):
tmp = random.randint(1, 6)
if tmp in [1, 6]:
dice_c += 1
cards = random.sample(card, 3)
for tmp in cards:
if tmp == 0:
card_c += 1
if coin_c == dice_c == card_c:
equal_c += 1
percent = 100*equal_c/tries
print(percent)
4Tego samego dnia pod wieczór swoje rozwiązanie nadesłał Cichy Fragles. Pomysł miał dobry, niestety walnął się odrobinę przy liczeniu prawdopodobieństw i wyszło mu 8.6%. Nie zaliczam.

Jeżeli chcesz do komentarza wstawić kod, użyj składni:
[code]
tutaj wstaw swój kod
[/code]
Jeżeli zrobisz literówkę lub zmienisz zdanie, możesz edytować komentarz po jego zatwierdzeniu.