Wstyd się przyznać, ale przez ostatnich kilka dni (?tygodni? szczęśliwi czasu, wiadomo) kompletnie wessało mnie programowanie z elemelkiem. Zamiast, jak normalny człowiek, oglądać w wolnym czasie śmieszne koty na tyrurce albo szlajać się po bezdrożach, zasiadam do zaelemelkowanego VSC i szlifuję swoje stare projekty, które już dawno byłyby umarły śmiercią naturalną z braku wiedzy, czasu bądź też samozaparcia (a na ogół wszystkich trzech na raz).
Na pierwszy ogień poszła symulacja zderzenia dwóch galaktyk, którą napisałem sobie dawno temu, w czasach, kiedy o LLM-ach jeszcze się nikomu nie śniło. Symulacja jest bardzo uproszczona - zakłada bowiem całkowity brak oddziaływania między gwiazdami, skupiając się wyłącznie na grawitacji centralnych czarnych dziur.
Z tego, co gdzieś kiedyś czytałem jest to dość znany model i w miarę dobrze się sprawdza, jeżeli nie zależy nam na jakiejś wybitnej dokładności i chcemy się po prostu z grubsza dowiedzieć "a co by było gdyby". Zaletą jest znaczne uproszczenie matematyki, a co za tym idzie możliwość zasymulowania dziesiątek a nawet setek tysięcy gwiazd na maszynie domowej klasy.
No więc wrzuciłem kod do LLM-a i najpierw kazałem mu go porządnie udokumentować (czytaj: dodać komentarze), a zaraz potem dodać możliwość zatrzymania / ponownego uruchomienia symulacji spacją, żeby łatwiej robić screenshoty.
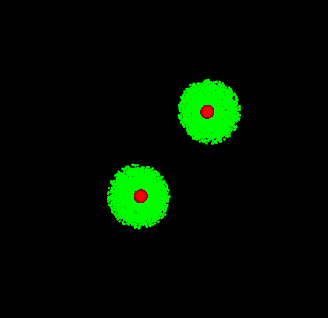
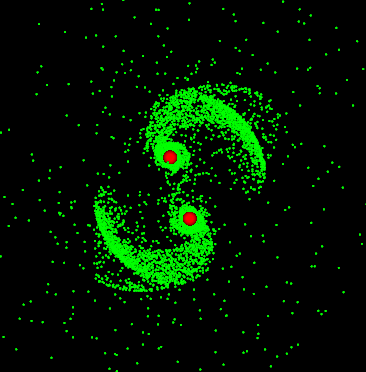
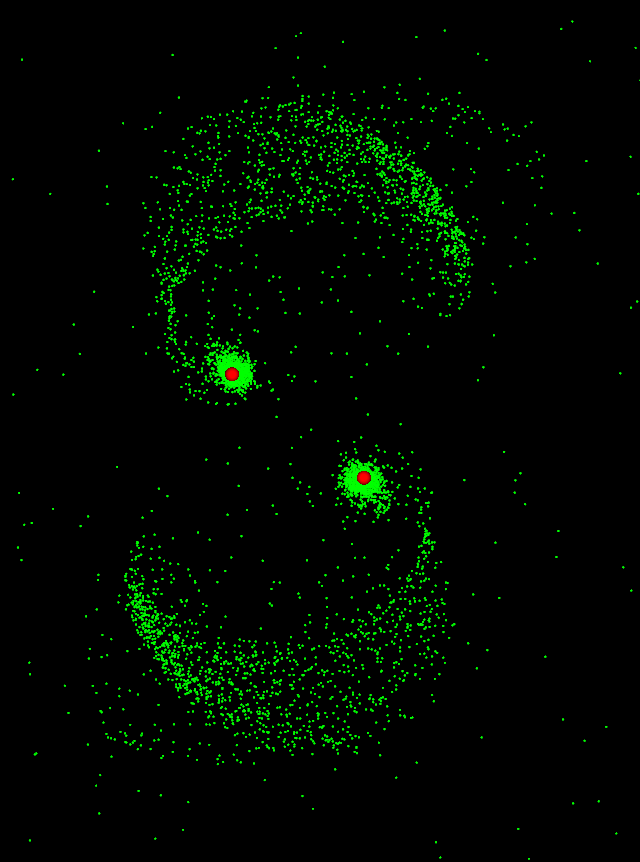
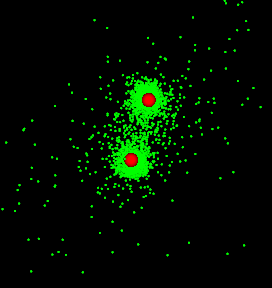
Jeżeli, Czytelniku sympatyczny, masz pod ręką komputer z kartą NVidia, poniższy kod powinien pójść od razu (zakładając, że masz zainstalowane numpy i taichi):
import taichi as ti
import numpy as np
# Initialize Taichi
ti.init(arch=ti.gpu)
# Constants
G = 1.0 # Gravitational constant (scaled)
PI = 3.141592653589793 # Value of pi
NUM_STARS = 20000 # Total stars
NUM_PER_GALAXY = NUM_STARS // 2
MASS_BH = 1e6 # Mass of black holes
DT = 0.001 # Time step
RADIUS_SCALE = 20.0 # Scale for initial star distribution
WINDOW_SIZE = 1200 # Visualization window size
# Fields
positions = ti.Vector.field(2, dtype=ti.f32, shape=NUM_STARS) # Star positions
velocities = ti.Vector.field(2, dtype=ti.f32, shape=NUM_STARS) # Star velocities
bh_positions = ti.Vector.field(2, dtype=ti.f32, shape=2) # Black hole positions
bh_velocities = ti.Vector.field(2, dtype=ti.f32, shape=2) # Black hole velocities
forces = ti.Vector.field(2, dtype=ti.f32, shape=NUM_STARS) # Forces on stars
# Initialize positions and velocities
@ti.kernel
def initialize():
# Black holes
bh_positions[0] = ti.Vector([-200.0, 0.0]) # Left galaxy
bh_positions[1] = ti.Vector([200.0, 0.0]) # Right galaxy
bh_velocities[0] = ti.Vector([0.0, -10.0])
bh_velocities[1] = ti.Vector([0.0, 10.0])
# Stars for left galaxy
for i in range(NUM_PER_GALAXY):
theta = ti.random() * 2 * PI
radius = ti.random() * RADIUS_SCALE
x = bh_positions[0].x + radius * ti.cos(theta)
y = bh_positions[0].y + radius * ti.sin(theta)
positions[i] = ti.Vector([x, y])
# Tangential velocity for circular orbit
speed = ti.sqrt(G * MASS_BH / (radius + 1e-5))
velocities[i] = ti.Vector([-speed * ti.sin(theta), speed * ti.cos(theta)])
# Stars for right galaxy
for i in range(NUM_PER_GALAXY, NUM_STARS):
theta = ti.random() * 2 * PI
radius = ti.random() * RADIUS_SCALE
x = bh_positions[1].x + radius * ti.cos(theta)
y = bh_positions[1].y + radius * ti.sin(theta)
positions[i] = ti.Vector([x, y])
# Tangential velocity for circular orbit
speed = ti.sqrt(G * MASS_BH / (radius + 1e-5))
velocities[i] = ti.Vector([-speed * ti.sin(theta), speed * ti.cos(theta)])
# Update positions and velocities
@ti.kernel
def update():
# Update forces on stars from black holes
for i in range(NUM_STARS):
forces[i] = ti.Vector([0.0, 0.0])
for j in range(2): # Each black hole
r_vec = bh_positions[j] - positions[i]
r = r_vec.norm() + 1e-5 # Avoid division by zero
f = G * MASS_BH / (r * r)
forces[i] += f * r_vec.normalized()
# Update star positions and velocities
for i in range(NUM_STARS):
velocities[i] += forces[i] * DT
positions[i] += velocities[i] * DT
# Update black hole positions and velocities
for i in range(2):
r_vec = bh_positions[1 - i] - bh_positions[i] # Force from the other black hole
r = r_vec.norm() + 1e-5
f = G * MASS_BH * MASS_BH / (r * r)
acc = f / MASS_BH * r_vec.normalized()
bh_velocities[i] += acc * DT
bh_positions[i] += bh_velocities[i] * DT
# Visualization
window = ti.ui.Window("Galaxy Collision", (WINDOW_SIZE, WINDOW_SIZE))
canvas = window.get_canvas()
scene = ti.ui.Scene()
camera = ti.ui.make_camera()
# gui = ti.GUI("Galaxy Collision", (WINDOW_SIZE, WINDOW_SIZE))
initialize()
paused = False
while window.running:
if window.get_event(ti.ui.PRESS):
if window.event.key == ti.ui.SPACE:
paused = not paused
if not paused:
update() # Physics update
camera.position(0.0, 0.0, 1000.0)
camera.lookat(0.0, 0.0, 0.0)
scene.set_camera(camera)
scene.point_light(pos=(0.0, 0.0, 1000.0), color=(1, 1, 1))
# Render black holes and stars
scene.particles(bh_positions, radius=5, color=(1.0, 0.0, 0.0))
scene.particles(positions, radius=1, color=(0.0, 1.0, 0.0))
canvas.scene(scene)
window.show()
I to wszystko w parę minut. Żyjemy w ciekawych czasach.
Tak, tak, wiem. Czym większy projekt, tym większa szansa, że elemelek zacznie produkować błędy. W dodatku czym elemelek sprytniejszy, tym błędy trudniejsze do wyłapania na wczesnym etapie i nagle się okazuje, że samolot już w powietrzu, a zatankowany tylko do połowy i trzeba awaryjnie wodować.
Niemniej jednak do małych, personalnych projektów elemelki, uważam, nadają się już od dość dawna. Polecam.
P.S. Kolega z pracy, który na programowaniu klient-serwer tudzież na webie zna się jak kura na pieprzu, wyelemelkował sobie niedawno w dwa dni swoją własną karcianą grę online, w przeglądarce i Wogle. Nie żeby na niej zarobić, tylko po to, żeby sobie od czasu do czasu pograć z synem, któremu strzeliła osiemnastka i się wyniósł z domu. Historia prawdziwa i z pierwszej ręki.
Jeżeli chcesz do komentarza wstawić kod, użyj składni:
[code]
tutaj wstaw swój kod
[/code]
Jeżeli zrobisz literówkę lub zmienisz zdanie, możesz edytować komentarz po jego zatwierdzeniu.