Dziś spróbuję oświecić Cię, sympatyczny Czytelniku, w kwestii tajemniczego okrągłego ciasteczka, czyli zagadki matematycznej o nieskończenie długim mnożeniu, które w efekcie daje skończoną, chociaż niewymierną, liczbę Pi.
Oryginalna zagadka:
A tutaj symulacja pierwszego tysiąca czynników w Excelu:
Zanim jednak zacznę, uprzedzę, że osiągnięcie owego zen nie będzie bezbolesne. Może się okazać, że niektórzy z Was po drodze zasną lub uciekną.
Powód: w matematyce jest znacząca różnica między dowodem trywialnym a elementarnym. Różne matematyczne blogi spłonęły pożogą kłótni o znaczenie tych dwóch pojęć, ale wreszcie udało się uzyskać jaki-taki konsensus. Otóż dowód trywialny polega na tym, że jest krótki i zwięzły, i oczywisty - dla tych, którzy "siedzą" w matematyce po uszy i znają się na różnych zaawansowanych metodach, których na próżno by szukać w szkolnych programach nauczania. Natomiast dowód elementarny to taki dowód, który używa metod prostych, znanych większości ludzi ze szkół podstawowych i średnich. Jednak elementarność dowodu nie oznacza jego zwięzłości - rozumowanie w dowodzie elementarnym może ciągnąć się kilometrami. Na chłopski rozum, coś jakby porównać wykopanie dużej dziury w ziemi za pomocą koparki przemysłowej z wykopaniem tej samej dziury łyżką do zupy. Nie każdego stać na koparkę, ale każdy ma łyżkę do zupy. Potrwa to "odrobinę" dłużej, ale w końcu się uda.
No więc właśnie. Dowód na zbieżność naszego iloczynu do wartości Pi/2 pokażę za pomocą metod elementarnych, ponieważ tylko takie są dostępne mojemu misiowemu rozumkowi. Obejdzie się bez całek, trygonometrii i bardziej zaawansowanych zwierząt. Wystarczy umiejętność dodawania, rozwiązywania prostych równań z jedną niewiadomą oraz - na samym końcu - twierdzenie Pitagorasa oraz wzór na pole koła. Będzie więc w miarę łatwo, ale nie na skróty.
OK, zaczynamy.
Zaczniemy od przypomnienia co sssssso właśśśśsiwie chozzzzi.
Chozzzzi o to, żeby wykazać równość:
(1) \( \displaystyle \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \ldots = \frac{\pi}{2}\)
Przy okazji, dla ułatwienia, oznaczymy sobie lewą stronę powyższego równania jako W. Dlaczego akurat W? Okaże się później, cierpliwości.
A więc:
(2) \( \displaystyle W = \frac{2}{1} \cdot\frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \ldots \)
Zauważamy, że ponieważ elementy na pozycjach parzystych są mniejsze od jedności, iloczyn cząstkowy zmniejsza się za każdym razem, kiedy mnożymy przez element parzysty. Analogicznie zwiększa się, jeżeli mnożymy przez element nieparzysty,
Zaczniemy od zdefiniowania sobie następującego iloczynu pomocniczego:
\( \displaystyle s_n = \frac{3}{2} \cdot \frac{5}{4} \cdot \ldots \cdot \frac{2n-1}{2n-2}\)Przyjmiemy też, że \( s_0 = 0\) oraz \( \textstyle s_1 = 1\)
Wnikliwy Czytelnik zauważy, że \( \textstyle s_n \) to nic innego jak iloczyn odwrotności kolejnych elementów W na pozycjach parzystych. A Czytelnik niewnikliwy właśnie to sprawdził, zerkając w górę 😉
W kolejnym kroku rozumowania zauważymy, że iloczyn nieparzystej liczby elementów (2) można przedstawić jako:
\( \displaystyle \frac{2n}{s_n^2} = \frac{2^2 \cdot 4^2 \ldots (2n)}{1 \cdot 3^2 \ldots (2n-1)^2} > W \)Podobnie iloczyn parzystej liczby elementów to:
\( \displaystyle \frac{2n-1}{s_n^2} = \frac{2^2 \cdot 4^2 \ldots (2n-1)^2}{1 \cdot 3^2 \ldots (2n-3)^2 \cdot (2n-1)} < W \)Ważny szczegół w powyższych dwóch nierównościach to brak kwadratu w ostatnim czynniku w liczniku pierwszej z nich oraz w ostatnim czynniku w mianowniku drugiej nierówności. Proszę sobie na spokojnie jeszcze raz obejrzeć (2) i zgrokować, że to faktycznie działa.
Z powyższych dwóch nierówności wynika, że:
(3) \( \displaystyle \frac{2n-1}{W} < s_n^2 < \frac{2n}{W}\)
Jeżeli jeszcze nie śpimy, bijemy sobie brawo, ponieważ właśnie dotarliśmy do okolic połowy naszego rozumowania. Nierówność (3) jest kluczowa: ustawia ona \(\textstyle s_n^2\) w konkretnych granicach.
Skoro dotarliśmy aż tutaj, zbudujemy sobie teraz kolejny poziom abstrakcji. Zaczyna się robić ciekawie[citation needed].
Skoro mamy zdefiniowane \( \textstyle s_n \), zdefiniujemy sobie teraz różnicę między dwoma kolejnymi elementami \( \textstyle s_n \) oraz \( \textstyle s_{n+1} \):
\( \displaystyle a_n = s_{n+1} - s_n = s_n \cdot (\frac{2n+1}{2n} - 1) = \frac{s_n}{2n} = \frac{1}{2} \cdot \frac{3}{4} \ldots \frac{2n-1}{2n}\).Zauważamy, że:
(4) \( \displaystyle a_i a_j = \frac{j+1}{i+j+1} a_i a_{j+1} + \frac{i+1}{i+j+1} a_{i+1} a_j \)
Skąd się wzięło (4)?
Trzeba sobie podstawić definicję \(s_n\) do \(a_{i+1}\) oraz \(a_{j+1}\) i wówczas po prawej stronie (4) otrzymamy:
\(a_i a_j (\frac{2j+1}{2(j+1)} \cdot \frac{j+1}{i+j+1} + \frac{2i+1}{2(i+1)} \cdot \frac{i+1}{i+j+1}) = a_i a_j\)Co się stanie, jeżeli zaczniemy rekurencyjnie podstawiać \( a_n \) z równości (4) dla coraz większych n?
Otóż stanie się to:
(5) \(1 = a_0^2 = a_0 a_1 + a_1 a_0 = a_0 a_2 + a_1^2 + a_2 a_0 = \ldots \\ = a_0 a_n + a_1 a_{n-1} + \ldots + a_n a_0\)
Skąd to wynika?
Jeżeli zaaplikujemy (4) do każdego składnika po prawej stronie (5), dostaniemy:
\( (a_0 a_n + \frac{1}{n} a_1 a_{n-1}) + (\frac{n-1}{n} a_1 a_{n-1} + \frac{2}{n} a_2 a_{n-2}) + \ldots \\ + (\frac{1}{n} a_{n-1} a_1 + a_n a_0) \)Po uproszczeniu powyższego, wychodzi \(a_0 a_n + \ldots + a_n a_0\).
Podsumujmy dotychczasowe dokonania:
- Zdefiniowaliśmy sobie pomocniczy iloczyn \(s_n\) oraz ustaliliśmy dwie wartości, między którymi zawsze znajduje się \(s_n^2\)
- Zdefiniowaliśmy sobie \(a_n\) jako różnicę między dwoma kolejnymi \(s_n\).
- Ustaliliśmy, że suma iloczynów \(a_0 a_n + \ldots + a_n a_0\) wynosi dokładnie 1, dla dowolnie dużego n.
Co dalej?
Dalej zmieniamy nieco front, bierzemy ołówek i zaczynamy rysować!
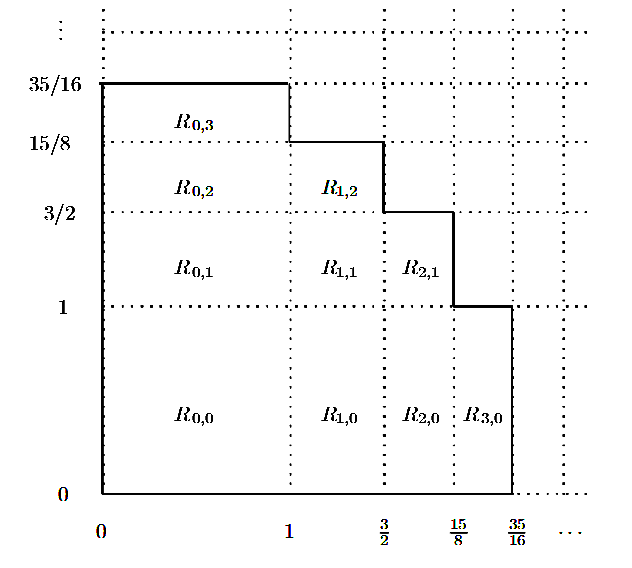
Powyższy rysunek to nic innego jak linie poziome oraz pionowe przecinające zarówno oś X jak i Y w punktach odpowiadających kolejnym wartościom \(s_n\). Proste te podzieliły nam pierwszą ćwiartkę układu współrzędnych na prostokąty \(R_{i,j}\), których dolny lewy wierzchołek znajduje się w punkcie \((s_i, s_j)\), a górny prawy w punkcie \((s_{i+1}, s_{j+1})\).
Jak widać pole powierzchni każdego z tych prostokątów wynosi \(a_i a_j\).
Z równości (5) wiemy, że suma pól prostokątów \(R_{i,j}\), których indeksy i, j sumują się do tego samego n jest zawsze równa 1 (na obrazku powyżej: pole \(R_{0,0} = 1\), pola \(R_{0,1} + R_{1, 0} = 1\), pola \(R_{0,2} + R_{1, 1} + R_{2, 0} = 1\) i tak dalej).
Zatem jeżeli weźmiemy wszystkie prostokąty \(R_{i,j}\) dla których suma indeksów jest mniejsza od n, wynikowa figura będzie miała pole powierzchni równe dokładnie n. Oznaczmy sobie taką figurę jako \(P_n\).
Zewnętrzne wierzchołki figury \(P_n\) to punkty \((s_i, s_j)\), dla których i + j = n + 1.
Z twierdzenia Pitagorasa wiemy, że odległość każdego z tych punktów od punktu (0,0) wynosi:
\( \sqrt{s_i^2 + s_j^2}\)Z nierówności (3) wiemy też, że powyższy pierwiastek jest na pewno mniejszy od:
\(\sqrt{\frac{2(i+j)}{W}} = \sqrt{\frac{2(n+1)}{W}}\).Analogicznie, wewnętrzne wierzchołki figury \(P_n\) są punktami \((s_i, s_j)\), dla których i + j = n. Rozumując identycznie jak w poprzednim kroku wnioskujemy, że są one odległe od początku układu współrzędnych o więcej niż:
\(\sqrt{\frac{2(i+j-1)}{W}} = \sqrt{\frac{2(n-1)}{W}}\).Powyższe dwie nierówności prowadzą do wniosku, że figura \(P_n\) zawiera w sobie ćwiartkę koła o promieniu \(\sqrt{\frac{2(n-1)}{W}}\), a także mieści się w całości w innej, większej ćwiartce koła o promieniu \(\sqrt{\frac{2(n+1)}{W}}\).
Ponieważ pole ćwiartki koła wynosi \(\frac{\pi r^2}{4}\), otrzymujemy następujące ograniczenie górne i dolne dla pola powierzchni figury \(P_n\):
\(\frac{\pi (n-1)}{2W} < n < \frac{\pi (n+1)}{2W}\)Powyższe ograniczenie jest prawdziwe dla każdego n, z czego wynika:
\( W = \frac{\pi}{2} \), co kończy dowód.
Na zakończenie winien jestem jeszcze wyjaśnienie dlaczego ów nieszczęsny nieskończony iloczyn oznaczyliśmy literką W. Otóż stało się tak na cześć matematyka Johna Wallisa, żyjącego na przełomie XV i XVI wieku, który zasłynął między innymi wprowadzeniem do zapisu matematycznego symbolu nieskończoności (\( \infty \)). Skonstruował również wiele interesujących nieskończonych ciągów, szeregów, iloczynów i im podobnych tworów, między innymi właśnie ten, którego dowód tu pokazałem.
A tu oryginał dowodu.

Jeżeli chcesz do komentarza wstawić kod, użyj składni:
[code]
tutaj wstaw swój kod
[/code]
Jeżeli zrobisz literówkę lub zmienisz zdanie, możesz edytować komentarz po jego zatwierdzeniu.