Ukryte pary

https://xpil.eu/43BZR 📋

Dzięki niedawnemu komentarzowi Buttera do tego wpisu, udało mi się niechcący natrafić na kolejną interesującą technikę eliminowania kandydatów w Sudoku. Tym razem chodzi o ukryte pary - technikę wymagającą sporej spostrzegawczości oraz cierpliwości (z cyfr od 1 do 9 da się ułożyć trzydzieści sześć różnych par), ale czasem niezbędną przy rozwiązywaniu trudnych układów.

Układ pokazany przez Buttera jest faktycznie piekielnie ciężki i nawet nie będę próbował pokazać jak go rozwiązać krok po kroku (aczkolwiek jeżeli ktoś jest zainteresowany, polecam darmową aplikację HoDoKu). Jednak już w pierwszym kroku da się zastosować technikę ukrytych par.

Oto szczegóły:

Przyjrzyjmy się kwadratowi r2c1 (czyli kwadrat 9x9 w pierwszej kolumnie, drugim rzędzie):

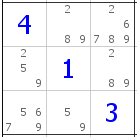Dla uproszczenia, wpisałem już wszystkie dopuszczalne cyfry w każdej z komórek tego kwadratu. W zasadzie nic z nich na pierwszy rzut oka nie wynika - jest tylko jedna para (5-9), nie ma żadnej wspólnej trójki i tak dalej. Dupa blada, zdawałoby się.

A jednak, jak się okazuje, nie taka dupa i nie taka blada. Przyjrzyjmy się bowiem gdzie znajdują się wszystkie szóstki i siódemki. Jak widać, szóstka z siódemką siedzą sobie w dolnym lewym rogu, a także w górnym prawym - i nigdzie więcej. 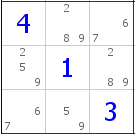To oznacza, że jeżeli w jednej z tych dwóch komórek wpiszemy szóstkę, w drugiej musimy wpisać siódemkę i na odwrót. Ponadto, jeżeli w którąkolwiek z tych dwóch komórek wpiszemy cokolwiek poza szóstką lub siódemką, dostaniemy układ sprzeczny (ponieważ pozostanie tylko jedna komórka z szóstką i tylko jedna - ta sama - komórka z siódemką).

Na tej podstawie możemy wyeliminować z tych dwóch komórek wszystkie inne cyfry, o tak:

Nudy...

https://xpil.eu/43BZR 📋