Zagadkę, którą tydzień temu postawiłem przed p.t. Czytelnictwem blogu można rozwiązać na kilka sposobów.
Sposób pierwszy: policzyć algorytmem. Na przykład Pythonem:
dzień, zostało = 1, 1
while zostało > 0:
zrobione = 2*zostało/(366-dzień)
zostało -= zrobione
print(dzień, zrobione, zostało)
dzień += 1
W wyniku zobaczymy, że ostatnia praca została wykonana w dniu numer 364, a więc w przedostatni dzień roku:
1 0.005479452054794521 0.9945205479452055 2 0.005464398615083547 0.989056149330122 3 0.005449345175372573 0.9836068041547494 4 0.005434291735661599 0.9781725124190879 5 0.005419238295950625 0.9727532741231373 6 0.0054041848562396515 0.9673490892668977 7 0.005389131416528678 0.961959957850369 8 0.005374077976817704 0.9565858798735514 ... 358 0.00010537407797681763 0.00031612223393045287 359 9.032063826584368e-05 0.0002258015956646092 360 7.526719855486973e-05 0.00015053439710973948 361 6.021375884389579e-05 9.032063826584369e-05 362 4.5160319132921845e-05 4.5160319132921845e-05 363 3.0106879421947898e-05 1.5053439710973947e-05 364 1.5053439710973947e-05 0.0
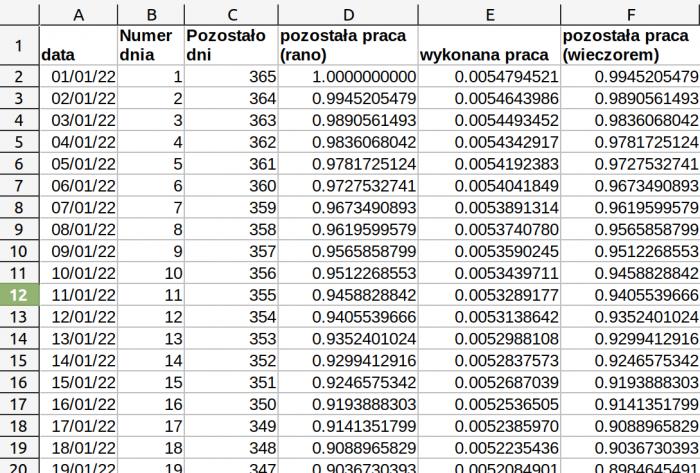
Sposób drugi: policzyć w arkuszu. Na przykład tak:
...
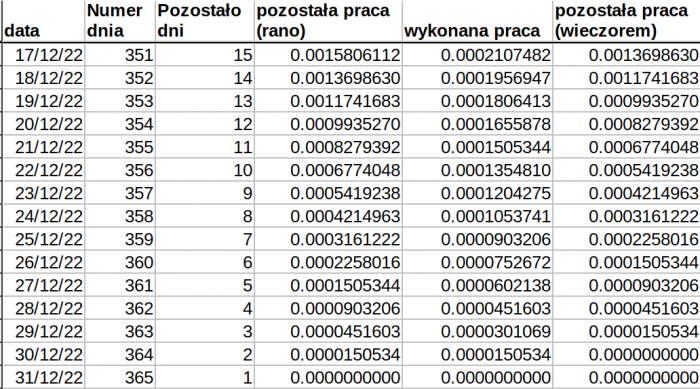
Też widać, że na koniec 364 dnia cała praca została wykonana.
Zerknijmy jeszcze na wykres pozostałej pracy w czasie:

Pomarańczowa część wykresu pokazuje ilość pozostałej pracy przy podejściu "normalnym" tj. liniowym, kiedy codziennie wykonujemy 1/365 zadania. Niebieska - przy podejściu jak w zagadce.
Okazuje się, że owszem, na początku "zaoszczędzamy" całkiem sporo czasu wykonując więcej pracy niż wynikałoby to ze średniej dziennej. Ale ilość pozostałej pracy stale się zmniejsza, a wyliczenie dziennej pracy do wykonania opiera się na tym właśnie, co pozostało; czym bliżej końca tym mniej pracy wykonujemy. Dokładnie w połowie roku, drugiego lipca, czyli w dniu numer 183, niebieska krzywa osiąga stromiznę linii pomarańczowej i od tego dnia wykonujemy codziennie mniej niż 1/365 zadania, a więc "przepada" to, co "nadgoniliśmy" dotychczas:
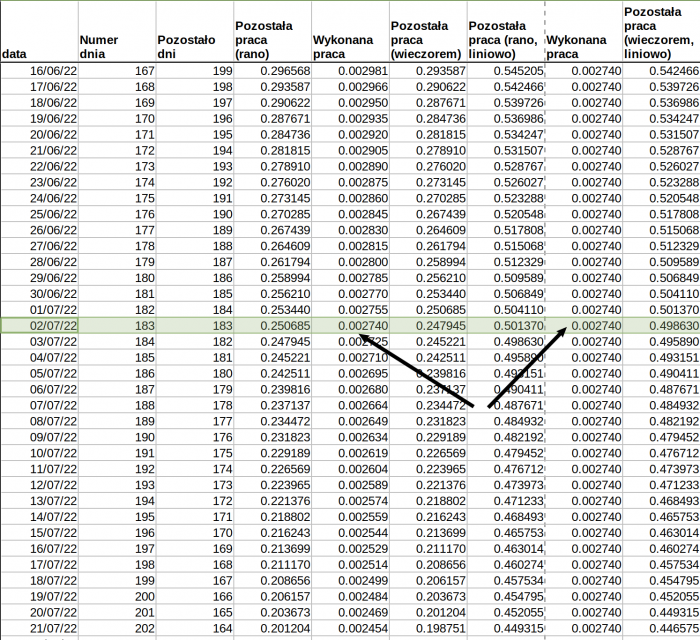
Ale - jak zresztą zasugerowałem w treści samej zagadki - można ją rozwiązać w pamięci, bez pomocy arkuszy kalkulacyjnych czy w ogóle komputerów!
A jak?
A no tak: skoro każdego dnia wykonujemy ułamek pracy wyliczany jako dwukrotność pracy pozostałej podzieloną przez liczbę pozostałych dni, to dopóki ta liczba pozostałych nie osiągnie dwójki, nigdy nie wykonamy całej pracy. A liczba pozostałych dni osiąga dwójkę w 364 dniu, czyli 30 grudnia rano, na dwa dni przed końcem roku. W tym dniu wykonamy 2/2 pozostałej pracy czyli w Sylwestra mamy wolne.
A jak Wam poszło?
Szybko. I same poprawne odpowiedzi!
1Waldek wygrał tę rundę, przysyłając poprawne rozwiązanie jako pierwszy, zaledwie w kilka godzin po publikacji zagadki:

2Również jeszcze tego samego dnia swoją odpowiedź nadesłał Rafał. A konkretnie dwie, pierwszą błędną, przymykam oko, a zaraz potem drugą, poprawną. Plusik za zauważenie własnego błędu i szybką poprawkę!

3Jeszcze się dobrze nie zrobił wieczór, a już pokazał się trzeci rozwiązujący. Cichy idzie na rekord jeśli chodzi o zwięzłość odpowiedzi 🙂

4Nazajutrz Rozie, bez pudła:

5Chwilę potem rekordowo krótkie rozwiązanie nadesłał Piotr:

6Potem dwa dni ciszy, wyczerpała się pula zwyczajowych rozwiązujących. Aż tu nagle poprawne rozwiązanie odgadł Zielak:

Aż zgłupiałem i musiałem wrzucić do translatora tytuł tego okienka „Leave a Comment” – jednak żadnego idiomu nie zobaczyłem… To pewnie dlatego, że u nas komentarze w okienku edycyjnym nadal się pisze, a nie zostawia. Pozostawiony komentarz może się poczuć smutny, samotny lub opuszczony. Wrażliwym osobnikom może zrobić się go żal. Paru romantyków wznieci na Albumie akcję ratunkową i… pominę parędziesiąt stron beletrystyki i przejdę do kody: ukamienują cię.
Piękne jest to, że mój, wspaniały i precyzyjny na ogół, translator DeepL też zgłupiał doszczętnie i tępo tłumaczy „opuść komentarz” oraz „osamotnij komentarz” jako „Leave a Comment”. Żadnych niuansów – czysto łopatologicznie, według smartfoniarzowych prymitywizmów językowych. Aż opada rzyć…
Hola, to tylko dygresja – przecież nie o tym miałem pisać. Ale o tym tak:
Jeżeli liczbę 2 z twojego zadania nazwiemy „licznik”, czyli L, a liczbę 366 – „mianownik”, czyli M, to można napisać ogólny wzór na pracę wykonaną w dniu n: X*L/(M-n). To X (reszta zadania do wykonania) łatwo da się wyliczyć w arkuszu, tak jak ty to zrobiłeś w rozwiązaniu zadania.
Jeśli ktoś myśli, że dla M=366 (jak w zdaniu) i L=3 otrzymamy wynik 363 to ma rację, a dla L=4 wynik 362, to też się nie myli. Ale dla większych L zaczynają się dziać dziwne rzeczy (dla którego to się zaczyna?).
Na logikę powinno zawsze być tak, że koniec, to: M-L. Ale taka logika okazuje się zwodnicza.
Proszę (zadanie uzupełniające), niech ktoś ambitny wyjaśni jasno, jednoznacznie i do końca porąbaną logikę tego zadania – czyli rezultaty uzyskiwane dla dowolnych L i M – powiedzmy na początek, że L=M, ujemne, rzeczywiste i zespolone – to brzmi, jak żart, ale tylko brzmi, gdyż większość tych przypadków jest – rzecz jasna – sprzeczna, ale nie wszystkie. Miłego Riemannowania…
Waldek
P.S. 1 Przypadek ogólny jest tak chory, że podczas rozwiązywania rozbolały mnie włoski przy gruczołach potowych. Jeśli ktoś dba o higienę, to nie radzę zabierać się za to zadanie.
P.S. 2 Poza tym spoko – nadal czuję się dobrze.
A u mnie od razu przetłumaczył poprawnie. Ciekawe czemu tak.
https://imgur.com/a/riNLxlH
Zadanie dodatkowe nr 2:
Należy odtworzyć oryginalną treść mojej poprzedniej wiadomości, wiedząc, że xpilowy edytor „Leave a Comment” usunął znaki większości i mniejszości. Bez tych znaków moje poprzednie wyznania nie mają żadnego sensu…
Zgłębiam tę zagadkę, a im bardziej ją poznaję, tym mniej ją rozumiem… Niby wszystko jest oczywiste, a cały czas wyskakują dziwadełka, które trudno ogarnąć.
Żeby każdy mógł chociaż liznąć tej dziwności, to proszę sobie policzyć w arkuszu kalkulacyjnym coś takiego:
Przypomnę wzór na pracę wykonaną w dniu n: L/(M-n)X_n, gdzie:
– L: licznik ułamka, w zadaniu było L=2
– M: liczba o 1 większa od liczby dni w roku. Na Ziemi M=365+1=366, ale na Marsie będzie inaczej.
– X_n – część zadania pozostała do wykonania w dniu n rano. Jest to po prostu 1 – suma dotychczas wykonanych zadań cząstkowych.
Jeżeli teraz zrobimy sobie tabelkę podobną do tej, którą zrobił Gospodarz prezentując rozwiązanie, ale zamiast L=2 zaczniemy wstawiać inne liczby, to zacznie się dziać. Oznaczając przez K numer dnia, w którym zakończy się zadanie otrzymamy z arkusza:
L=2 K=364
L=3 K=363
L=4 K=362
L=5 K=361
L=6 K=360
L=7 K=359
i wreszcie nieoczekiwane
L=8 K=357
Powinno być K=358, a nie jest! Dlaczego? To nielogiczne…
Wcześniej pytałem też o rozwiązanie w liczbach rzeczywistych. Metodą sprawdzania wyniku dla kolejnych cyfr po przecinku znalazłem liczbę:
L=7,087135221… dla której jeszcze K=359, ale już dla
L=7,087135222 będzie K=357.
Różnica tych L o 10^{-9} daje skokową zmianę K o 2. Nie ma, nawet w liczbach rzeczywistych płynnego przejścia przez K=358. Mówiąc inaczej K=358 jest niemożliwe. I można by na tym skończyć, gdyby nie kilka matematycznych zagwozdek:
1. Pierwsza, to wyprowadzenie prostego, jednoznacznego wzoru na pracę wykonaną do dnia n. Proste? Wcale nie, proszę spróbować.
2. Druga zagwozdka, to dla świrów, takich, jak ja – jak już ktoś się całkiem zagłębi w rachunki i wyniki z dziedziny liczb zespolonych – tam da się uzyskać K=358 (tak!) i wszystkie inne, ale z jednym, jedynym wyjątkiem K=183… I tu na razie poległem. Może wejdę w kwaterniony?
Obstawiam, że masz gdzieś błąd we formule liczącej K. Pobawiłem się przed chwilą arkuszem i dla L=7 wyszło mi K=359, a dla L=8 K=358 (a nie, jak piszesz, 357). Testowałem dalej aż do L=11 i wszystko bez niespodzianek.
Ewentualnie ja mam gdzieś błąd w swojej formule…
Tu moje formuły: https://i.imgur.com/SR42dxn.png
A tutaj wyniki: https://i.imgur.com/HuncdWW.png
Pomysły?
P.S. Co do edycji komentarzy to pozbyłem się niedawno wtyczki WPDisquz (za drogo mnie kosztowała – płaciłem za rzeczy, których nie używałem), dlatego zniknęła możliwość edytowania. Dzisiaj dodałem inną wtyczkę, która pozwala na edycję komentarza w ciągu godziny od jego publikacji. Powinno być OK.
Wygląda na klasyczny problem z zaokrągleniami. Czyli, że błąd może nie tkwić w formule, a w narzędziu. Czyli wersja programu w którym jest arkusz itp. BTW możecie porównać na żywo np. na Google Sheets, bez przekazywania formuł w obrazkach.
W Pythonie także nie ma przeskoku o 2 dla L=8, więc to nie właściwość zagadki.