W odróżnieniu od poprzedniej zagadki planimetrycznej o dwóch prostokątach wpisanych w kwadrat, podział pizzy literą "A" nie jest zagadnieniem całkiem trywialnym. Na szczęście jednak nie musimy uciekać się do żadnych wyższych zaklęć - odrobina trygonometrii i zdrowego rozsądku powinny w zupełności wystarczyć.
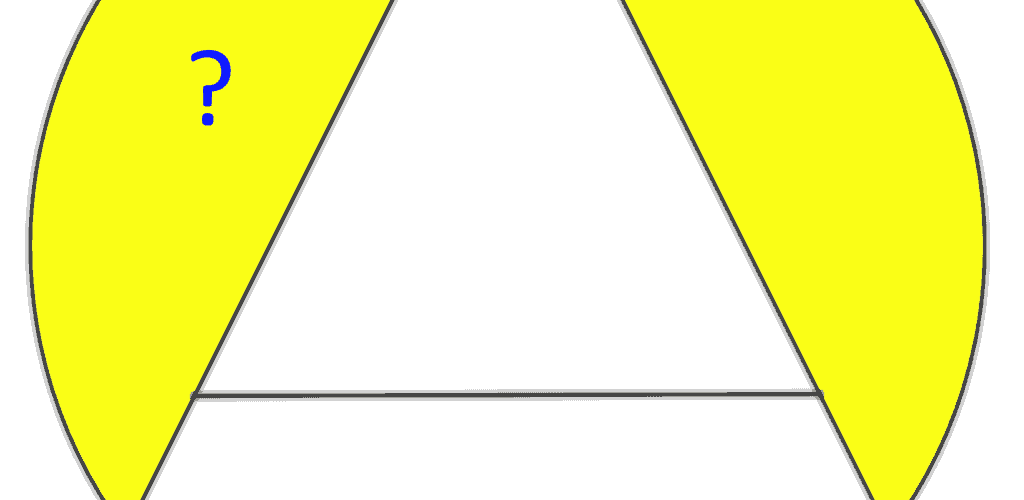
Pizzę napoczniemy od łatwiejszej strony czyli przeanalizujemy sobie dwa symetryczne kawałki po bokach:

Każdy z dwóch podświetlonych na żółto segmentów oparty jest na jakimś kącie. Zwyczajowo oznacza się ten kąt φ.
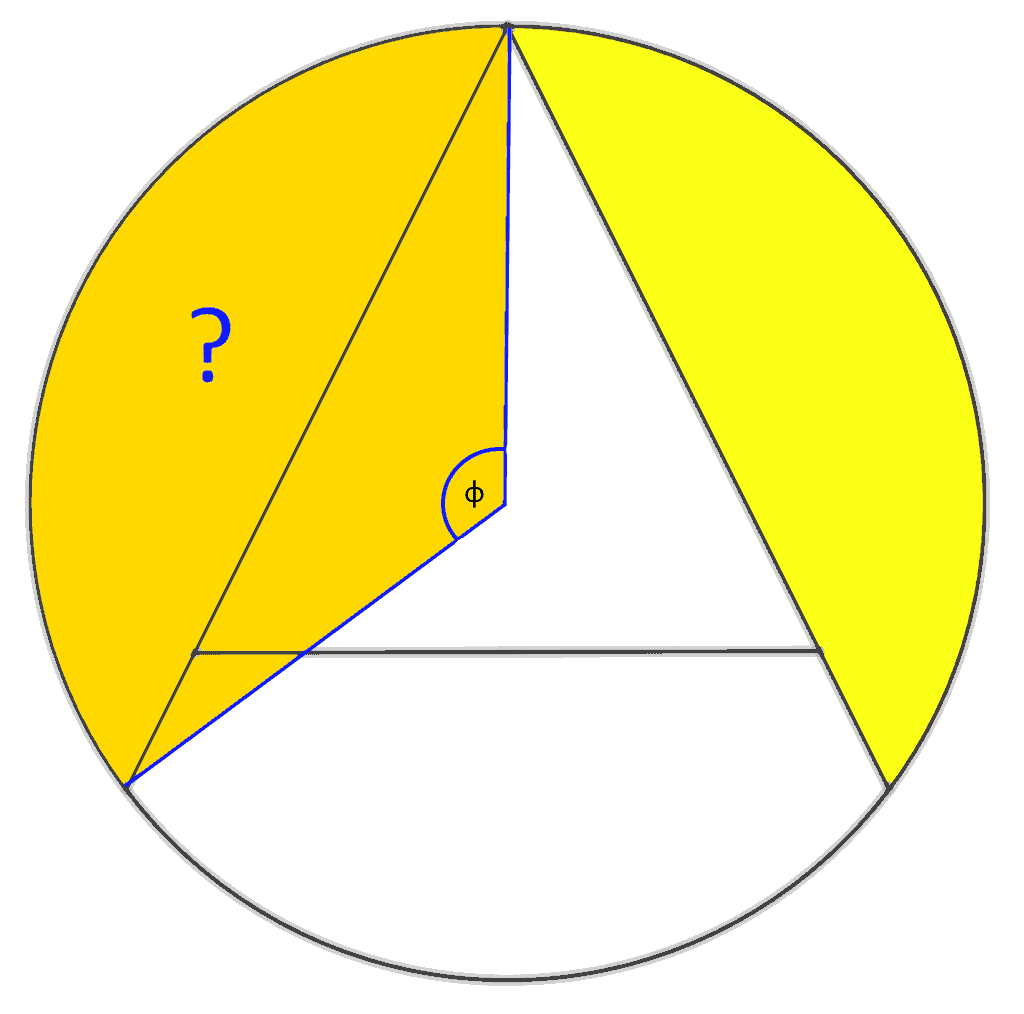
Z lekcji matematyki pamiętamy[citation needed], że pole powierzchni wycinka pizzy koła (pomarańczowy kawałek na rysunku powyżej) to \(\frac{1}{2} R^2 \phi\)
Jeżeli od tego odejmiemy teraz pole powierzchni trójkąta równoramiennego, zostanie nam sama "czapeczka", o którą nam chodzi.
Jeżeli mamy naprawdę dobrą pamięć, oraz mieliśmy solidnego nauczyciela matematyki w szkole średniej, być może pamiętamy jeszcze, że pole powierzchni trójkąta równoramiennego z kątem φ między ramionami wynosi: \(\frac{1}{2} R^2 sin(φ)\), gdzie R jest długością ramienia (i szczęśliwie również promieniem pizzy koła w naszym zadaniu). Odejmując jedno od drugiego dostajemy w końcu upragniony wzór na pole powierzchni żółtego kawałka pizzy: \(R^2 \frac{φ - sin(φ)}{2}\).
Żeby sobie nie komplikować życia, możemy przyjąć, że pizza ma kształt koła o promieniu R = 1, dzięki czemu powyższe staje się po prostu: \(\frac{φ - sin(φ)}{2}\).
Z treści zagadki wiemy, że jest to ćwierć powierzchni całej pizzy. Jeżeli cała powierzchnia ma \(\pi\), wówczas możemy zapisać:
\(\frac{φ - sin(φ)}{2} = \frac{\pi}{4}\)Co po podstawieniu i wyliczeniu daje nam:

Tak więc wiemy już, że dwa boczne kawałki pizzy, odcięte ukośnymi ramionami litery A, oparte są na kącie równym mniej więcej 2.31 radianów (mniej więcej 132 stopnie)
Przyjrzyjmy się teraz wnętrzu litery A - składa się ono z górnej części, która jest trójkątem równoramiennym, oraz dolnej, będącej lekko "trzepniętym" trapezem z łukiem zamiast podstawy.
Jeżeli boczne segmenty oparte są na kącie mniej więcej 132 stopnie każdy, to łącznie zużywa nam to około 264 stopni. Pozostaje około 96 stopni na kąt, pod którym "widać" tą łukowatą podstawę "trapezu". Z twierdzenia o kącie środkowym wiemy zatem, że kąt przy wierzchołku tego dużego trójkąta w środku ma około 48 stopni.
Oznaczymy sobie teraz długość podstawy tego trójkąta jako 2x. Podzielimy go na pół w pionie...

Co wiemy?
Wiemy, że pole połowy tego trójkąta wynosi \(\frac{\pi}{8}\) (z warunków zadania). Wiemy też, że kąt przy górnym wierzchołku to okolice 24 stopni. Tangens tego kąta to x/h a powierzchnia trójkąta to x*h/2. Robimy z tego układ dwóch równań z dwiema niewiadomymi...

I dostajemy wynik:

Ujemne wartości możemy odrzucić, czyli 2x wynosi mniej więcej 1.18 i to jest ostateczna (acz przybliżona) odpowiedź.
Jeżeli ktoś będzie na tyle zajadły, żeby wrzucić w Wolframa dokładne wartości kątów, wyjdzie mu (bądź jej), że 2x wynosi z dość dużą dokładnością 1.177863.
Do zagadki podeszło trzech Czytelników; tylko jeden (Waldek) podał poprawną odpowiedź, tok rozumowania w zasadzie identyczny z wyżej opisanym tylko skompresowany do absolutnego minimum:
Odcinek koła na kącie x doprowadza do: x-sin(x)=pi/2
stąd x=2,30988
https://www.wolframalpha.com/input/?i=x-sinxpi2
Z trójkąta w "A" długość szczebelka = sqrt( pi*tan((pi-x)/2)
Jeden z Czytelników anonimowo podniósł problem nieuczciwego podziału tej pizzy, ponieważ trzy kawałki mają krawężnik, a jeden - nie:
Uprzejmię informuję, iż taki podział budzi mój osobisty niepokój. Jedna osoba dostanie pizzę bez krawężników, co jest bardzo nie fair. I to też powinno być wzięte pod uwgaę w tym 'niesprawiedliwym choć może i równym' dzieleniu!
Uprzejmie objaśniam, że Antek - jako jedyny z tej czwórki - miał uczulenie na krawężniki, więc się akurat dobrze złożyło, że wszyscy mieli imiona na literę A a nie, dajmy na to, na X czy F.
Do kolejnej zagadki, która pokaże się tu już w piątek, zapraszam ludzi mających jakie takie pojęcie o programowaniu komputerów. Trzeba będzie bowiem przeczesywać całkiem spore zbiory danych w poszukiwaniu pewnych dopasowań. Przyda się też polityczny atlas Polski z 2000 roku (lub nowszy).
W moim odnośniku do Wolframa, który zacytowałeś, zostały pożarte nawiasy, znaki równości i dzielenia, więc link nie działa. To znaczy działa, ale tak głupio, że powinien się wstydzić.
Czy ja coś źle wkleiłem, czy to wina okienek edycyjnych usuwających „zbędne” elementy tekstu? Twój link działa dobrze…
Jak więc (na przyszłość) wklejać takie linki?
Nie jestem pewien. Może przepuścić je przez jakiegoś skracacza?