Bierzemy okrąg o średnicy jeden.
Na jego obwodzie wybieramy (N+1) równo odległych od siebie punktów. Inaczej mówiąc dzielimy okrąg na (N+1) jednakowej długości łuków.
Wybieramy jeden z tych (N+1) punktów łączymy go za pomocą N cięciw z pozostałymi N punktami, o tak:
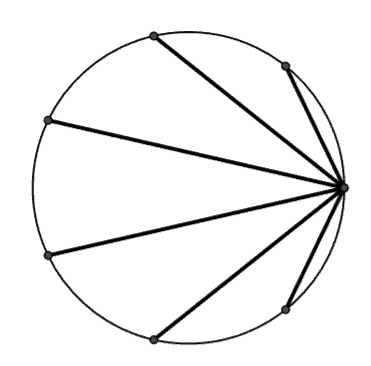
Następnie mnożymy przez siebie długości wszystkich N cięciw.
Co nam wyjdzie?
N!
(ale nie N silnia, tylko N ze zdziwionym wykrzyknikiem)
To jest ciekawostka numer jeden. Jeżeli jednak, Czytelniku, czytasz ten wpis uważnie od samego początku, na pewno kojarzysz, że w tytule jest nazwisko Fibonacciego. Czemu tak?
A no temu, że wystarczy nasz okrąg (razem z N cięciwami!) rozciągnąć wzdłuż stycznej w naszym wybranym punkcie tak, żeby dostać jajko (zwane fachowo elipsą) o wysokości \(\sqrt{5}\), żeby zaczęły się dziać prawdziwe cuda.

Tu mamy nasz okrąg z poprzedniego obrazka rozciągnięty w pionie do \(\sqrt{5}\)
Bierzemy teraz wszystkie cięciwy i - podobnie jak poprzednio - mnożymy ich długości. Co wyjdzie?
Otóż wyjdzie...
... fanfary...
\( N F_N\)czyli po naszemu N - krotność N-tej z kolei liczby Fibonacciego.
Aby dowieść prawdziwości tego stwierdzenia należy skorzystać z lematu, który mówi, że jeżeli elipsę podzielimy na łuki jak wyżej, to iloczyn długości cięciw wynosi \( N \frac{A^N - B^N}{A-B}\), gdzie (A-B) oraz (A+B) to odpowiednio krótsza i dłuższa średnica elipsy. W naszym przypadku długości te dają N-krotność wzoru Bineta (więcej szczegółów tutaj: !klik!), który generuje kolejne liczby Fibonacciego dla kolejnych N.
Trochę to poskracałem, bo nie chciało mi się wgryzać w te wszystkie cyferki (jestem leniwy), ale zapewniam, że wszystko się zgadza.
Magia, panie.
Jeżeli chcesz do komentarza wstawić kod, użyj składni:
[code]
tutaj wstaw swój kod
[/code]
Jeżeli zrobisz literówkę lub zmienisz zdanie, możesz edytować komentarz po jego zatwierdzeniu.