Na różne tematy już tu pisaliśmy, ale o ślimakach to chyba jeszcze nie było.
Dziś znów zagadka, bo trenowanie szarej substancji jest ważne, a i ubawić się przy tym można.
No więc tak...
Jest sobie sześć ślimaków.
Każdy z nich znajduje się na wierzchołku sześciokąta foremnego o boku długości jednego metra:

No i teraz tak: w pewnym momencie wszystkie ślimaki równocześnie zaczynają iść w kierunku swojego najbliższego sąsiada (zgodnie z ruchem wskazówek zegara):
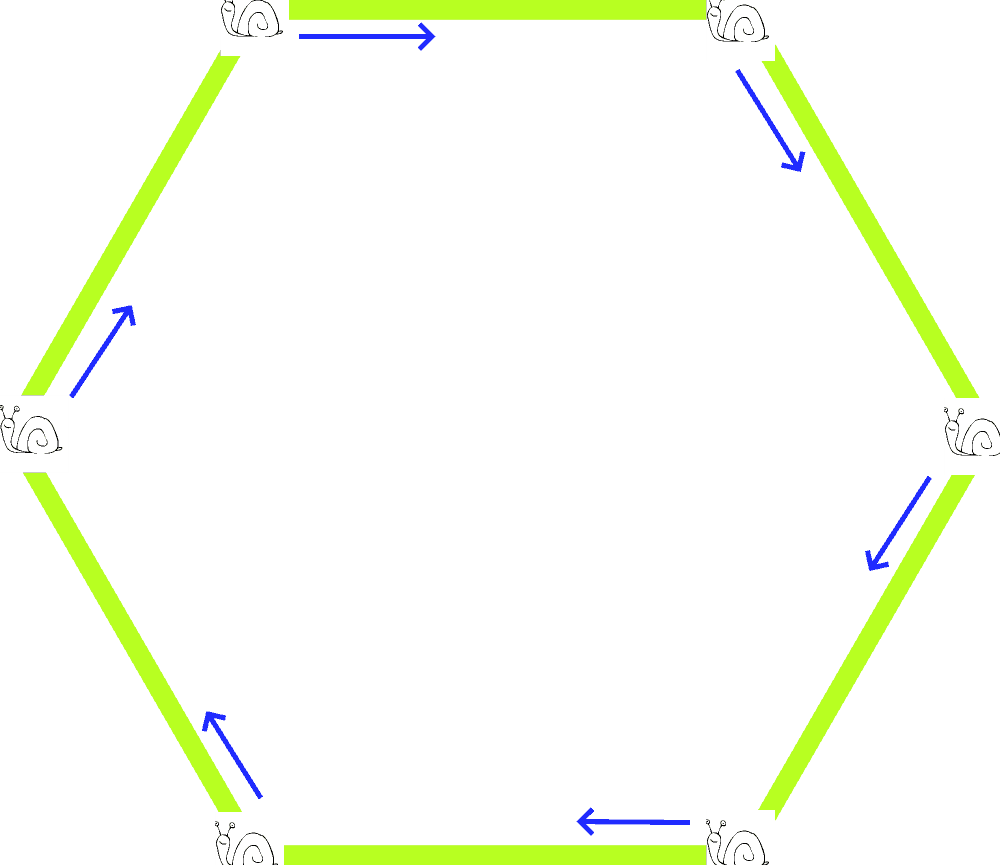
W każdej chwili każdy ślimak przemieszcza się dokładnie w stronę sąsiada, a więc poruszają się one po czymś na kształt coraz bardziej zacieśniających się spiral:
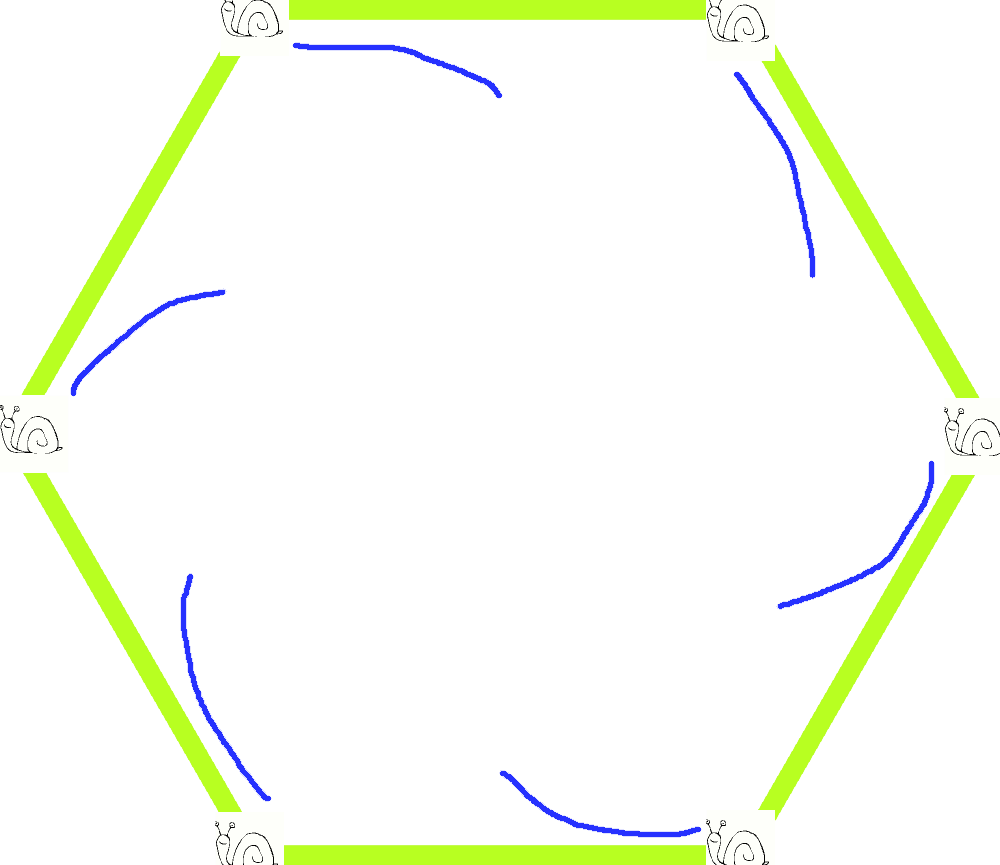
Każdy ślimak porusza się z tą samą, niezmienną prędkością. Ponieważ wszystkie wystartowały w tym samym momencie i każdy jest w identycznej sytuacji co wszystkie pozostałe, każdy przejdzie taką samą drogę.
Pytanie: jaką odległość pokona każdy ze ślimaków od chwili startu do chwili, kiedy cała szóstka zetknie się w środku?
Zakładamy rzecz jasna, że rozmiar ślimaka jest pomijalnie mały w stosunku do wielkości sześciokąta (innymi słowy traktujemy każdego ślimaka jako punkt)
Czas - start!

Z czysto matematycznego punktu widzenia droga chyba będzie nieskończona – ślimaki cały czas będą tworzyć sześciokąt, coraz mniejszy i coraz bardziej obrócony wobec wyjściowego, relatywnie coraz szybciej malejący, ale nic ponadto. Chyba że prędkość ślimaków wpływa jakoś na kształt spirali, ale wydaje mi się, że nie powinna.
Natomiast jeśli założymy, że ślimaki nie są tak całkiem punktowe, tylko np. centymetrowe, to wystarczy policzyć, w jakim tempie maleje odległość między dwoma ślimakami, żeby wiedzieć po ilu metrach obwód tworzonego przez nie sześciokąta spadnie poniżej ich rozmiarów – ale nie mam pomysłu, jak to prosto policzyć, a przypominać sobie trygonometrii i liczyć na kartce mi się nie chce. Może później na coś wpadnę.
Polecam poczytać o paradoksie Zenona powinno to rozwiać wątpliwości dlaczego droga będzie skończona.
Spirala jak najbardziej może być nieskończona (np. jeśli zawęża się o połowę z każdym obrotem), a paradoks Zenona nie ma tu nic do rzeczy.
Czy to znaczy, że jeżeli zbliżasz jedną rękę do drugiej najpierw o 1/2 odległości później 1/4, a następnie o 1/8 i tak dalej. To pierwsza ręka przebędzie nieskończenie długą drogę ?
Jeżeli spirala zawężałaby się o połowę z każdym obrotem, to znaczy że kąt, pod którym ślimak patrzyłby na drugiego ślimaka zmieniałby się z upływem czasu, co nie jest prawdą (wszystkie ślimaki są cały czas na wierzchołkach sześciokąta foremnego, więc kąt jest stały).
Paradoks Zenona jak najbardziej na miejscu.
Nie myślę zupełnie, dopiero uwaga o kącie patrzenia odblokowała mi klepkę w mózgu – faktycznie, droga musi być skończona, bo odległość między ślimakami maleje liniowo.
A w jakim tempie? Cóż, jeśli ślimak przesuwa się o wektor [x, 0], to następny ślimak w tym samym czasie robi wektor [x / 2, x * sqrt(3) / 2], więc odległość między nimi maleje o ciut ponad x/2 (gdzie „ciut ponad” dąży do zera przy x znacznie mniejszym od odległości), z czego wynika, że ślimaki powinny w drodze do środka pokonać dwukrotność długości boku.
Żeby to sprawdzić, napisałem na szybko skrypt, który wygenerował takie coś: https://i.imgur.com/kpl2nhw.jpg – a liczba iteracji na dojście do środka, przy prędkości ślimaka jeden piksel na iterację, faktycznie wyniosła dwa razy długość boku w pikselach.
Piękne! Rzuć kodem w wolnej chwili.
Mniej brute forcem pasowałoby chyba przejście na układ biegunowy lub w dziedzinę liczb zespolonych. Czyli nasza krzywa przyjęłaby wzór R*(ctg(alfa)*theta) gdzie R jest odległością ślimaka od początku układu współrzędnych dla theta = 0, w naszym przypadku będzie R = 1. Natomiast kąt alfa to kąt natarcia który jak już stwierdziliśmy jest stały i wynosi 60 stopni. Teraz taką krzywą trzeba by zcałkować od -nieskończoności do 0 w rezultacie uzyskamy wynik 2.
Zmieniając 2pi na 6pi Wolfram podaje 2. 000000 jako wynik przybliżony. Wszystko się zgadza!
Proszę bardzo: https://ufile.io/9g5r5o22